Параллелепипед – особый вид геометрической фигуры, обладающий прямыми гранями и параллельными боковыми гранями. В каждом параллелепипеде, независимо от его размеров, есть диагонали. Диагональ – это прямая линия, соединяющая противоположные вершины фигуры. Знание диагонали параллелепипеда может быть полезно в различных сферах жизни, например, при строительстве, дизайне интерьеров или выборе устройства для хранения вещей.
Определить диагональ параллелепипеда можно, зная его измерения – длину, ширину и высоту. Для этого достаточно использовать формулу вычисления длины диагонали правильного параллелепипеда. Формула нахождения длины диагонали представляет собой применение теоремы Пифагора к трём сторонам параллелепипеда.
Как применить формулу и что нужно учесть при определении диагонали параллелепипеда? Как воспользоваться результатом измерений в практической деятельности? В данной статье мы рассмотрим все основные аспекты этой темы и дадим полезные советы, которые помогут вам правильно определить диагональ параллелепипеда по измерениям. Присоединяйтесь!
Способы определить диагональ параллелепипеда по измерениям
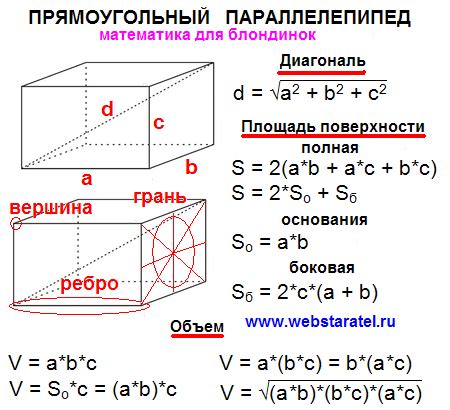
1. Теорема Пифагора
Если известны все три измерения - длина, ширина и высота параллелепипеда, то можно использовать теорему Пифагора для определения диагонали. Применение формулы: диагональ = квадратный корень из (длина² + ширина² + высота²).
2. Теорема косинусов
Если известны углы между сторонами параллелепипеда, можно использовать теорему косинусов для определения диагонали. Применение формулы: диагональ = квадратный корень из (сторона₁² + сторона₂² - 2 * сторона₁ * сторона₂ * cos(угол)).
3. Методы измерения
Если доступны только измерения сторон параллелепипеда, можно воспользоваться прямым измерением с использованием линейки или измерительной ленты. Последовательно измерьте каждую сторону параллелепипеда и используйте формулу диагонали, описанную выше в теореме Пифагора.
Выбор оптимального способа определения диагонали параллелепипеда зависит от доступных данных и предпочтений. Важно помнить, что точность измерений будет влиять на точность определения диагонали.
Измерение сторон

Для определения диагонали параллелепипеда необходимо измерить длину, ширину и высоту каждой из его сторон:
- Используйте измерительную ленту или линейку для измерения длины первой стороны параллелепипеда. Запишите полученное значение.
- Аналогично измерьте ширину второй стороны параллелепипеда и запишите это значение.
- Измерьте высоту третьей стороны параллелепипеда и запишите измерение.
После того, как вы измерили все стороны параллелепипеда, вы можете расчитать его диагональ, используя известную формулу:
Диагональ = √(длина^2 + ширина^2 + высота^2)
Подставьте значения, которые вы получили при измерениях, в данную формулу и выполните расчет.
Теперь у вас есть эффективный метод измерения диагонали любого параллелепипеда!
Формула нахождения диагонали

Для определения диагонали параллелепипеда необходимо знать его измерения: длину, ширину и высоту. Диагональ параллелепипеда можно найти с использованием классической формулы диагонали трехмерной фигуры.
Формула нахождения диагонали параллелепипеда выглядит следующим образом:
Диагональ = √(Длина² + Ширина² + Высота²)
Где √ обозначает операцию извлечения квадратного корня.
Применив данную формулу, можно точно определить длину диагонали параллелепипеда, исходя из его измерений. Используйте измерения в тех же единицах измерения (например, сантиметры или дюймы), чтобы получить правильный результат.
Зная диагональ параллелепипеда, можно более точно определить его геометрические характеристики и использовать эту информацию для решения различных задач.
Примеры решения задачи

Рассмотрим несколько примеров, как определить диагональ параллелепипеда по измерениям:
Пример 1:
Пусть у нас есть параллелепипед с длиной сторон А = 5, шириной B = 3 и высотой C = 4. Для нахождения диагонали используем формулу:
Диагональ = √(A² + B² + C²)
Подставляя значения:
Диагональ = √(5² + 3² + 4²) = √(25 + 9 + 16) = √50 ≈ 7.071
Таким образом, диагональ параллелепипеда равна примерно 7.071 единицы длины.
Пример 2:
Пусть у нас есть параллелепипед с длиной сторон А = 8, шириной B = 6 и высотой C = 10. Снова используем формулу для нахождения диагонали:
Диагональ = √(A² + B² + C²)
Подставляя значения:
Диагональ = √(8² + 6² + 10²) = √(64 + 36 + 100) = √200 ≈ 14.142
Таким образом, диагональ параллелепипеда равна примерно 14.142 единицы длины.
Пример 3:
Пусть у нас есть параллелепипед с длиной сторон А = 12, шириной B = 9 и высотой C = 7. Используем формулу для нахождения диагонали:
Диагональ = √(A² + B² + C²)
Подставляя значения:
Диагональ = √(12² + 9² + 7²) = √(144 + 81 + 49) = √274 ≈ 16.552
Таким образом, диагональ параллелепипеда равна примерно 16.552 единицы длины.
Надеюсь, примеры помогут вам понять, как определить диагональ параллелепипеда по его измерениям.
Важные моменты при измерении

1. Используйте правильные инструменты. Для измерения диагонали можно использовать гибкую ленту или линейку. Убедитесь, что инструмент четко показывает метки и имеет точную шкалу измерения.
2. Записывайте измерения. Во время измерений рекомендуется записывать результаты, чтобы легко отслеживать и сравнивать значения. Это поможет избежать ошибок и сделать более точные расчеты.
3. Измерьте диагональ в разных направлениях. Чтобы получить более точные данные, рекомендуется измерять диагональный размер параллелепипеда в нескольких разных направлениях. Это поможет учесть возможные отклонения и получить более средний и точный результат.
4. Используйте подходящую точку измерения. Выберите точку на каждой из сторон параллелепипеда, с которой будете измерять диагональ. Расположите инструмент измерения вдоль этих точек и проведите линию через противоположные точки. Это поможет получить более точное измерение диагонали.
5. Учтите возможные ошибки округления. При измерениях существует вероятность небольших ошибок округления, особенно при использовании инструментов с ограниченной точностью. Поэтому рекомендуется округлять результаты до ближайшего десятых или сотых долей, чтобы получить более точные значения.
Следуя этим простым рекомендациям, вы сможете правильно измерить диагональ параллелепипеда и получить точные значения его размеров. Это позволит вам более эффективно использовать параллелепипед в различных целях, таких как строительство или 3D моделирование.
Рекомендации при работе с нестандартными фигурами

Работа с нестандартными фигурами, такими как параллелепипеды, требует дополнительного внимания и точности. Вот несколько рекомендаций, которые помогут вам определить диагональ таких фигур:
1. Используйте теорему Пифагора. С помощью этой теоремы вы можете вычислить длину диагонали параллелепипеда, используя длины его сторон. Первым шагом определите длину диагонали основания параллелепипеда с помощью теоремы Пифагора для плоскости. Затем найдите длину диагонали между углами основания и верхней точкой параллелепипеда. Сложите эти две длины, чтобы получить итоговую длину диагонали. |
2. Воспользуйтесь трехмерным подходом. Для нестандартных фигур, таких как параллелепипеды, более эффективным подходом может быть использование трехмерных координат. Рассмотрите параллелепипед как систему трех пересекающихся плоскостей и определите точки, через которые проходят диагонали. Затем вычислите расстояние между этими точками с помощью трехмерной теоремы Пифагора. |
3. Применяйте правило косинусов. Если у вас есть информация о длинах сторон и углах параллелепипеда, вы можете использовать правило косинусов для вычисления длины диагонали. Зная значения сторон и углов, вы можете определить косинус угла между двумя диагоналями, а затем использовать формулу для вычисления длины диагонали. |
4. Используйте специализированные инструменты. Существуют также специализированные инструменты, такие как калькуляторы или программы для вычисления диагоналей нестандартных фигур. Если вам нужно регулярно работать с такими фигурами, это может быть хорошим вариантом для экономии времени и упрощения процесса определения диагонали. |
При работе с нестандартными фигурами, важно быть внимательными и аккуратными. Следуйте указанным выше рекомендациям и используйте подходящие методы для определения диагонали параллелепипеда, чтобы получить точный результат.
- Перед началом измерений убедитесь, что параллелепипед расположен на ровной поверхности.
- Тщательно измерьте длину, ширину и высоту параллелепипеда в сантиметрах или любых других единицах измерения.
- Для определения диагонали параллелепипеда используйте теорему Пифагора: квадрат диагонали равен сумме квадратов двух других сторон.
- Вычислите сумму квадратов длины, ширины и высоты параллелепипеда.
- Извлеките квадратный корень из полученной суммы, чтобы определить длину диагонали.
Используя эти простые рекомендации, вы сможете определить диагональ параллелепипеда без необходимости дополнительных инструментов или сложных формул. Важно помнить, что точность измерений и правильное применение теоремы Пифагора позволят получить наиболее точный результат.