Диагональ параллелограмма - это отрезок, соединяющий две противоположные вершины этой фигуры. Он играет важную роль в геометрии и позволяет определить множество характеристик параллелограмма, например, его площадь и углы. Чтобы найти диагональ параллелограмма, необходимо знать длины его сторон и навыки работы с геометрическими формулами.

Существует несколько методов для определения диагонали параллелограмма. Один из них – использование теоремы Пифагора. Согласно этой теореме, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Применяя эту теорему к параллелограмму, можно выразить диагональ через длины его сторон.

Еще один метод состоит в использовании закона косинусов. Этот закон позволяет найти длину стороны треугольника, если известны длины двух других сторон и величина между ними образованного угла. Применяя закон косинусов к параллелограмму, можно найти длину диагонали, зная длины его сторон и угол между ними.

Как определить диагональ параллелограмма

Если известны длины сторон параллелограмма и угол между ними, можно использовать теорему косинусов для определения длины диагонали. Формула для вычисления диагонали параллелограмма выглядит следующим образом:

d = √(a^2 + b^2 - 2abcosθ)

где d - длина диагонали, a и b - длины сторон параллелограмма, θ - угол между этими сторонами.

Если известны только длины сторон параллелограмма, можно использовать теорему Пифагора для нахождения длины диагонали. Для этого нужно воспользоваться формулой:

d = √(a^2 + b^2)

где d - длина диагонали, a и b - длины сторон параллелограмма.

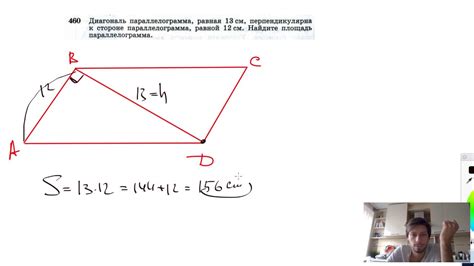
Зная длину диагонали параллелограмма, можно также определить его площадь. Формула для вычисления площади параллелограмма выглядит следующим образом:

S = a * h

где S - площадь параллелограмма, a - длина одной из его сторон, h - высота, проведенная к этой стороне.

Таким образом, зная длины сторон параллелограмма и угол между ними, можно определить длину его диагонали, а затем вычислить площадь. Эти формулы являются полезными при решении задач с использованием параллелограммов и позволяют получить точные значения и результаты.

Методы и формулы для нахождения

Существует несколько методов и формул, позволяющих найти длину диагонали параллелограмма:

1. По сторонам и углам: используя теоремы тригонометрии, можно выразить диагональ параллелограмма через длины сторон и углы параллелограмма. Наиболее часто используется теорема косинусов, которая позволяет найти длину диагонали по трем известным сторонам и углу между ними.

2. По координатам вершин: если известны координаты вершин параллелограмма, можно использовать формулу расстояния между точками, чтобы найти длину диагонали. Для этого необходимо найти координаты вершин, задать координаты диагональной точки и вычислить расстояние между ними.

3. По формуле пифагора: если известны длины сторон параллелограмма и одна из диагоналей, можно воспользоваться теоремой Пифагора, которая позволяет найти длину второй диагонали. Для этого необходимо знать длину одной диагонали и длины двух сторон, которые встречаются в ее конце.

Выбор метода и формулы для нахождения диагонали параллелограмма зависит от имеющихся данных и конкретной задачи, которую необходимо решить. Важно учитывать, что все формулы и методы основаны на математических принципах и позволяют получить точные результаты.