Прямоугольный треугольник – это треугольник, у которого один из углов равен 90 градусам. В прямоугольном треугольнике есть два катета и одна гипотенуза. Катеты – это стороны треугольника, образующие прямой угол, а гипотенуза – сторона, противолежащая прямому углу. Зная длины двух сторон, можно найти длину третьей стороны по теореме Пифагора.
Теорема Пифагора гласит: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Формула выглядит так: a^2 + b^2 = c^2, где a и b – длины катетов, а c – длина гипотенузы.
Чтобы найти катет или гипотенузу в прямоугольном треугольнике, нужно знать длину одной из сторон и применить соответствующую формулу. Например, если известны длины катета a и гипотенузы c, можно найти длину катета b, используя выражение b^2 = c^2 - a^2. Если известны длины катета b и гипотенузы c, можно найти длину катета a, используя выражение a^2 = c^2 - b^2.
Как найти катет и гипотенузу в прямоугольном треугольнике?
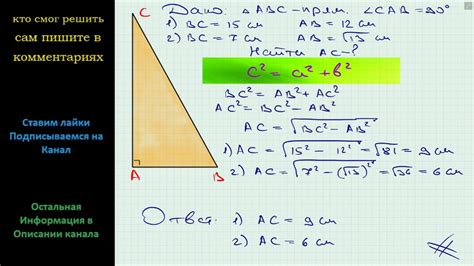
Теорема Пифагора гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Если известны значения двух сторон треугольника, можно использовать теорему Пифагора для нахождения третьей стороны. Например, если известны значения одного катета и гипотенузы, то квадрат второго катета можно найти, вычтя квадрат первого катета из квадрата гипотенузы. Далее можно найти значение второго катета, извлекая квадратный корень из найденного значения.
Аналогично, если известны значения обоих катетов, можно использовать теорему Пифагора для нахождения значения гипотенузы. Нужно сложить квадраты обоих катетов и извлечь из полученного значения квадратный корень.
Зная значения катета и гипотенузы, можно также использовать теорему Пифагора для нахождения значения второго катета. Квадрат второго катета будет равен разности квадрата гипотенузы и квадрата первого катета.
Используйте теорему Пифагора для нахождения значений катетов и гипотенузы в прямоугольном треугольнике и решайте геометрические задачи с уверенностью!
Пример прямоугольного треугольника
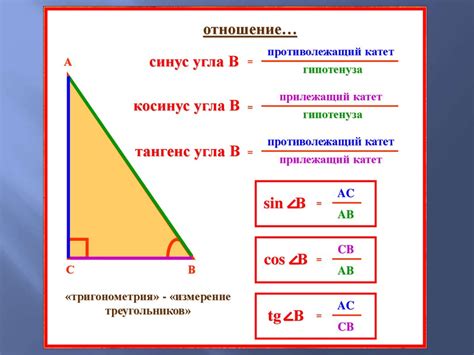
Допустим, у нас есть прямоугольный треугольник, у которого один катет равен 5, а гипотенуза равна 13. Мы будем искать длину другого катета.
Для решения этой задачи можем использовать теорему Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов, или в форме уравнения:
c² = a² + b²
Где c - гипотенуза, a и b - катеты.
В нашем случае значение гипотенузы уже известно - 13, один из катетов равен 5. Мы можем подставить эти значения в уравнение и решить его, чтобы найти второй катет:
13² = 5² + b²
169 = 25 + b²
b² = 144
b = √144
b = 12
Таким образом, второй катет прямоугольного треугольника равен 12.
Определение катета
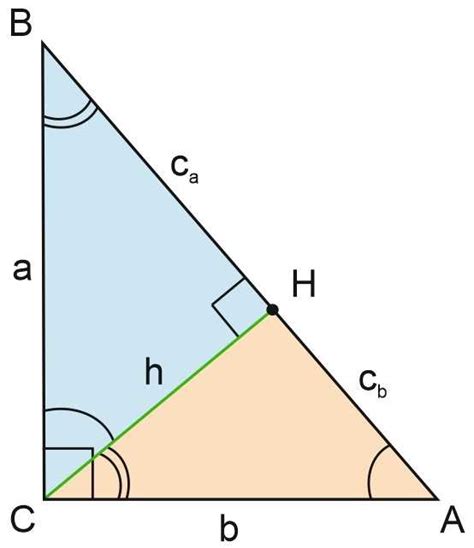
Катеты – это две стороны прямоугольного треугольника, которые образуют прямой угол. Один катет лежит напротив прямого угла, а другой катет соединяет противоположный угол с вершиной прямого угла.
Для определения катета в прямоугольном треугольнике можно использовать теорему Пифагора. Согласно этой теореме, катет в прямоугольном треугольнике можно найти, используя следующую формулу:
| a2 = c2 - b2 | ||
| a - катет | c - гипотенуза | b - другой катет |
Для определения значения катета необходимо знать значения гипотенузы и другого катета. Подставьте известные значения в формулу и решите уравнение, найдя катет.
Например, если гипотенуза треугольника равна 10, а другой катет равен 6, то можно найти значение первого катета:
| a2 = 102 - 62 |
| a2 = 100 - 36 |
| a2 = 64 |
| a = √64 |
| a = 8 |
Таким образом, первый катет в данном примере равен 8.
Определение гипотенузы
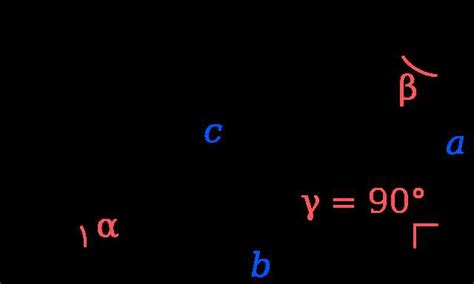
Чтобы найти гипотенузу, нужно знать длины двух других сторон треугольника - катетов. По теореме Пифагора гипотенуза равна квадратному корню суммы квадратов катетов:
гипотенуза (с) = √(катет1 (a)² + катет2 (b)²)
Например, если длина катета a равна 3, а длина катета b равна 4, то гипотенуза c будет равна:
с = √(3² + 4²) = √(9 + 16) = √25 = 5
Таким образом, гипотенуза в данном примере равна 5.
Формула нахождения катета
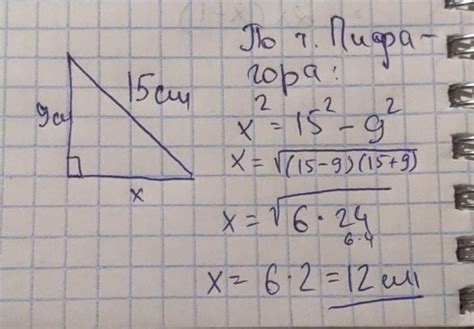
В прямоугольном треугольнике для нахождения катета с помощью известной гипотенузы и другого катета можно использовать теорему Пифагора:
Квадрат гипотенузы равен сумме квадратов обоих катетов:
c^2 = a^2 + b^2
где:
- c - гипотенуза треугольника
- a и b - катеты треугольника
Используя эту формулу, можно найти длину одного катета, если известна длина гипотенузы и другого катета.
Пример:
Дан прямоугольный треугольник с гипотенузой длиной 5 и одним из катетов длиной 3. Чтобы найти длину другого катета, мы можем использовать формулу квадрата гипотенузы:
c^2 = a^2 + b^2
Заменяем известные значения:
5^2 = 3^2 + b^2
Решаем уравнение:
25 = 9 + b^2
b^2 = 25 - 9
b^2 = 16
b = 4
Таким образом, в данном примере длина второго катета равна 4.
Формула нахождения гипотенузы
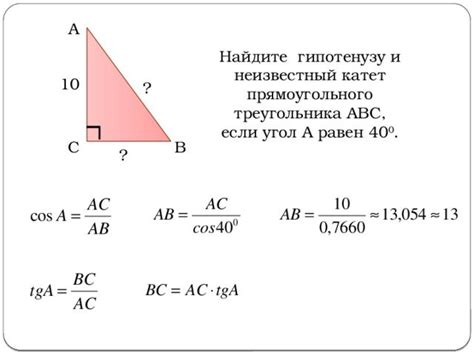
Формула нахождения гипотенузы в прямоугольном треугольнике называется теоремой Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов.
Математически данная формула записывается следующим образом:
c2 = a2 + b2
Где c обозначает гипотенузу, а a и b - катеты треугольника.
Для нахождения гипотенузы вам необходимо знать значения обоих катетов треугольника. Подставляйте их в формулу и решайте уравнение.
Таким образом, формула нахождения гипотенузы является основой для решения многих задач в геометрии и физике, связанных с прямоугольными треугольниками.
Примеры решения задач
Рассмотрим несколько примеров решения задач на нахождение катета и гипотенузы в прямоугольном треугольнике.
Пример 1:
Дано: гипотенуза (c) = 10, катет (a) = 6.
Найти: второй катет (b).
| Решение: | Формула: |
|---|---|
Используем теорему Пифагора: с^2 = a^2 + b^2. Подставляем значения: 10^2 = 6^2 + b^2. Вычисляем: 100 = 36 + b^2. Вычитаем 36 из обеих частей уравнения: 64 = b^2. Извлекаем корень из обеих частей уравнения: b = √64. Получаем: b = 8. | с^2 = a^2 + b^2 10^2 = 6^2 + b^2 100 = 36 + b^2 64 = b^2 b = √64 |
Пример 2:
Дано: гипотенуза (c) = 13, второй катет (b) = 5.
Найти: первый катет (a).
| Решение: | Формула: |
|---|---|
Используем теорему Пифагора: c^2 = a^2 + b^2. Подставляем значения: 13^2 = a^2 + 5^2. Вычисляем: 169 = a^2 + 25. Вычитаем 25 из обеих частей уравнения: 144 = a^2. Извлекаем корень из обеих частей уравнения: a = √144. Получаем: a = 12. | c^2 = a^2 + b^2 13^2 = a^2 + 5^2 169 = a^2 + 25 144 = a^2 a = √144 |
Таким образом, решение задач на нахождение катета и гипотенузы в прямоугольном треугольнике сводится к использованию теоремы Пифагора.
