Окружность - это геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от одной фиксированной точки, называемой центром окружности. Она является одной из самых изучаемых фигур в геометрии и находит применение в различных областях науки и техники.
При решении задач, связанных с окружностью, важную роль играет её длина, так как она позволяет определить множество её свойств и применить их при решении практических задач. Традиционно, для вычисления длины окружности используется число π (пи), которое является иррациональным числом и равно отношению длины окружности к её диаметру. Однако, есть способы вычисления длины окружности без использования числа π, которые позволяют получить более точные результаты и упростить вычисления.
Один из методов вычисления длины окружности без π основан на использовании длины хорды и расстояния от центра окружности до этой хорды. Если известна длина хорды и расстояние до неё от центра окружности, то существует специальная формула, позволяющая вычислить длину окружности. Такой подход особенно полезен в задачах, где измерения проводятся внутри окружности или недоступны точные данные о радиусе или диаметре.
Еще одним методом вычисления длины окружности без использования π является метод аппроксимации. При этом использование аппроксимаций позволяет приближенно определить длину окружности с заданной точностью, используя заранее подобранные коэффициенты или значения других математических функций. Такие методы часто применяются в инженерии и компьютерной графике для определения размеров окружностей на чертежах и моделях.
Что такое длина окружности?
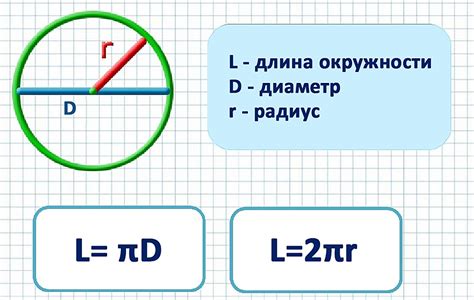
Формула для вычисления длины окружности состоит из умножения числа π на диаметр окружности. Однако, существуют методы и приближенные формулы, которые позволяют вычислить длину окружности без использования числа π.
Узнание длины окружности важно для многих областей науки и инженерии, таких как архитектура, строительство, машиностроение, а также для различных вычислений и расчетов в геометрии и тригонометрии.
Методы вычисления длины окружности без π
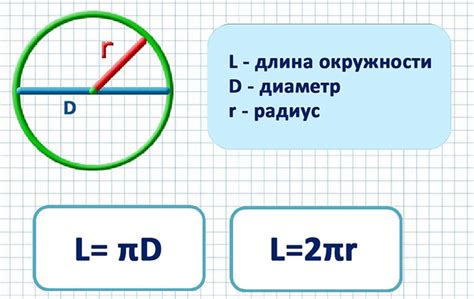
Для вычисления длины окружности без использования числа π существует несколько методов. Один из них основывается на использовании радиуса и угла окружности.
Если известен радиус окружности и ее центральный угол (в градусах или радианах), то длина окружности может быть вычислена по формуле:
L = 2 * r * π * (угол / 360)
Где L - длина окружности, r - радиус окружности, угол - центральный угол окружности в градусах или радианах.
Другой метод основан на использовании диаметра окружности. Если известен диаметр окружности, длина окружности может быть вычислена по формуле:
L = d * π
Где L - длина окружности, d - диаметр окружности.
Также существуют другие методы приближенного расчета длины окружности без использования π, такие как расчеты на основе аппроксимации или использование числа "три". Однако, эти методы не являются точными и могут быть полезны только для грубой оценки.
Метод 1: Использование диаметра
Для вычисления длины окружности по диаметру применяется следующая формула:
| Формула | Расшифровка | Пример |
|---|---|---|
| Длина окружности = Диаметр * π | Вычисление длины окружности как произведение диаметра на π | Длина окружности = 10см * 3.14 = 31.4см |
Данный метод основывается на равенстве отношений длины окружности к ее диаметру для всех окружностей. Коэффициент π представляет собой постоянное число, близкое к 3.14.
Используя этот метод, можно вычислять длину окружности, зная только значение ее диаметра. Но следует помнить, что результат будет приближенным, так как число π является иррациональным и имеет бесконечное количество десятичных знаков.
Метод 2: Использование радиуса и угла
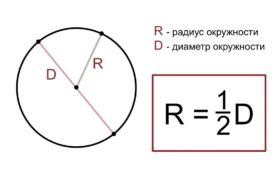
Для этого необходимо знать радиус окружности и указать величину угла в радианах. Затем можно использовать формулу:
Длина окружности = радиус * угол в радианах
Например, если радиус окружности равен 5 см, а угол между двумя точками на окружности равен 60 градусов (или π/3 радиан), то длина окружности можно вычислить следующим образом:
Длина окружности = 5 см * (π/3 радиан) = (5π/3) см ≈ 5,24 см
Таким образом, при использовании радиуса и угла можно получить приближенное значение длины окружности без использования числа π.
Примеры вычислений

Для расчета длины окружности без использования числа π можно воспользоваться различными методами. Вот несколько примеров:
Метод умножения диаметра на 3
Пусть у нас есть окружность с диаметром 10 единиц. Чтобы вычислить ее длину по этому методу, нужно умножить диаметр на 3:
Длина окружности = 10 * 3 = 30 единиц.
Метод сложения двух радиусов и умножения на 2
Пусть у нас есть окружность с радиусом 5 единиц. Чтобы вычислить ее длину по этому методу, нужно сложить два радиуса и умножить полученную сумму на 2:
Длина окружности = (5 + 5) * 2 = 20 единиц.
Метод умножения диаметра на число 3.14
Пусть у нас есть окружность с диаметром 6 единиц. Чтобы вычислить ее длину по этому методу, нужно умножить диаметр на число 3.14:
Длина окружности = 6 * 3.14 = 18.84 единиц.
Метод умножения радиуса на 2 и на число 3.14
Пусть у нас есть окружность с радиусом 8 единиц. Чтобы вычислить ее длину по этому методу, нужно умножить радиус на 2 и на число 3.14:
Длина окружности = 8 * 2 * 3.14 = 50.24 единиц.
Это только несколько примеров методов вычисления длины окружности без использования числа π. Выбор метода зависит от предоставленных данных и требуемой точности результата.
Пример вычисления длины окружности по заданным параметрам
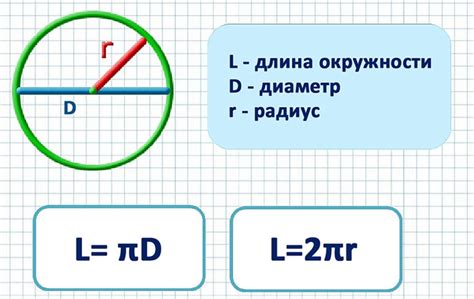
Для вычисления длины окружности без использования числа π, вам потребуется знать значение радиуса окружности. Это может быть любое число, представляющее длину отрезка, соединяющего центр окружности с её периметром.
Рассмотрим пример: имеется окружность с радиусом 10.
Чтобы найти длину окружности данного радиуса, можно воспользоваться формулой:
L = 2 * r * π
где L - длина окружности, r - радиус окружности, π - число пи.
В данном случае, поскольку мы не используем число π, помним, что отношение длины окружности к диаметру всегда является константой, известной как число π. Значит, можем воспользоваться уравнением:
L = 2 * r * (L/d)
где d - диаметр окружности. В нашем примере диаметр равен 20 (дважды радиус).
Таким образом, значение длины окружности будет:
L = 2 * 10 * (L/20) = 20*(L/20) = L
Полученный ответ будет равен диаметру окружности, то есть 20.
Пример вычисления длины окружности в задаче геометрии
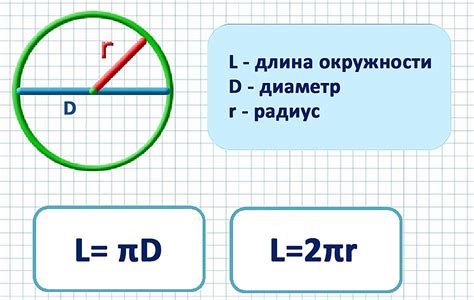
Однако, мы хотим вычислить длину окружности без использования π. Для этого, мы можем воспользоваться другой формулой: L = 2*R*c, где L - длина окружности, R - радиус окружности, а c - так называемое "отношение длины окружности к диаметру" или "математическая константа".
Значение c можно вычислить экспериментально или найти в таблице математических констант. Для большинства окружностей, значение c примерно равно 3.14 или 22/7.
Например, если у нас есть окружность с радиусом 10 см, мы можем вычислить длину окружности по формуле L = 2*10*3.14 = 62.8 см.
Таким образом, используя формулу L = 2*R*c, мы можем вычислить длину окружности без использования π.