Трапеция – это геометрическая фигура с двумя параллельными сторонами, которые называются основаниями. Одно из оснований трапеции может быть больше или меньше другого. Основание трапеции можно легко вычислить, если известны его средняя линия и одна из диагоналей. В этом математическом гайде мы расскажем, как правильно найти основание трапеции по средней линии и диагонали, и предоставим вам удобный бесплатный калькулятор для расчетов.
Для того чтобы найти основание трапеции по средней линии и диагонали, нужно знать следующую формулу:
Основание = [2 * площадь трапеции] / [длина диагонали]
Теперь разберемся более подробно в каждом шаге расчета основания трапеции.
Основные понятия
Прежде чем начать рассматривать методы расчета основания трапеции по средней линии и диагонали, необходимо разобраться в некоторых основных понятиях.
Трапеция - это выпуклый четырехугольник, у которого две противоположные стороны параллельны. Одна из параллельных сторон называется основанием, а другая - верхней базой. Другие две стороны называются боковыми сторонами.
Средняя линия трапеции - это линия, соединяющая середины боковых сторон.
Диагональ трапеции - это отрезок, соединяющий противоположные вершины.
Расчет основания трапеции по средней линии и диагонали позволяет определить размеры основания, используя известные значения средней линии и диагонали. Это может быть полезно при решении различных задач, связанных с геометрией и конструированием.
Метод 1: По средней линии и диагонали
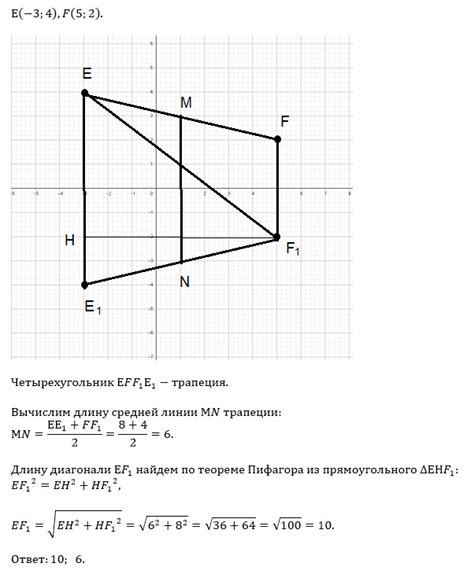
Расчет основания трапеции по средней линии и диагонали может быть выполнен по формуле. Используя данную формулу, можно определить значение основания, если известны значения средней линии (или высоты) и диагонали трапеции.
Предположим, что значения средней линии и диагонали трапеции равны l и d соответственно. Тогда основание трапеции (b) может быть вычислено с использованием следующей формулы:
| Формула для расчета основания: | b = (2 * l * d) / (l + d) |
|---|
Используя данный метод, можно быстро и легко определить значение основания трапеции при известной средней линии и диагонали. Для выполнения расчета можно воспользоваться специальным калькулятором, который автоматически выполнит все необходимые вычисления.
Если вам необходимо найти основание трапеции по средней линии и диагонали, вы можете воспользоваться бесплатным калькулятором, который предоставляется для расчетов. Просто введите значения средней линии и диагонали в соответствующие поля, и калькулятор автоматически рассчитает значение основания трапеции.
Метод 2: Бесплатный калькулятор

Если вам необходимо быстро и удобно рассчитать основание трапеции по средней линии и диагонали, вы можете воспользоваться бесплатным калькулятором. Это простой и эффективный способ получить точный результат без необходимости выполнять сложные математические расчеты.
Для использования калькулятора вам потребуется знать значения средней линии и диагонали. Введите эти значения в соответствующие поля калькулятора и нажмите кнопку "Рассчитать". Калькулятор моментально выполнит необходимые расчеты и выдаст вам результат - значение основания трапеции.
Воспользовавшись бесплатным калькулятором, вы экономите время и получаете точный результат расчетов. Этот метод особенно полезен, если вам необходимо рассчитать основание трапеции несколько раз или если вам нужно проделать расчеты для нескольких разных значений средней линии и диагонали.
| Средняя линия | Диагональ | Основание трапеции |
|---|---|---|
Калькулятор позволяет вам использовать любые значения средней линии и диагонали. Вы можете вводить числа как целые, так и десятичные. После нажатия кнопки "Рассчитать" результат появится в соответствующем поле.
Используя бесплатный калькулятор, вы сможете быстро и точно найти основание трапеции по средней линии и диагонали без необходимости выполнять сложные математические расчеты вручную.
Инструкция по использованию калькулятора

Чтобы найти основание трапеции по средней линии и диагонали, следуйте этим простым шагам с использованием нашего бесплатного калькулятора:
1. Введите значение средней линии в соответствующее поле. Средняя линия - это отрезок, который соединяет середины параллельных сторон трапеции.
2. Введите значение диагонали в соответствующее поле. Диагональ это отрезка, которые соединяет две непараллельные стороны трапеции.
3. Нажмите "Рассчитать" и дождитесь результатов.
4. В результате будут выведены значения основания трапеции.
5. Если вы хотите провести еще один расчет, очистите поля ввода и введите новые значения.
Теперь вы можете легко и быстро находить основание трапеции по средней линии и диагонали с помощью нашего бесплатного калькулятора! Пользуйтесь им в любое время, чтобы решать задачи и упрощать свою работу!
Примеры решений задач

Ниже приведены несколько примеров решения задач по нахождению основания трапеции по средней линии и диагонали:
Пример 1:
Известны длина средней линии трапеции и одна из ее диагоналей. Найдем длину основания трапеции.
Дано:
Средняя линия = 10 см
Диагональ = 8 см
Решение:
Пусть основания трапеции равны a и b, а средняя линия равна м.
Используя свойства трапеции, мы можем записать следующие формулы:
a + b = 2м (1)
Диагональ делит трапецию на два треугольника, поэтому мы можем записать две теоремы Пифагора:
a^2 - b^2 = 4 ^2 - 8 ^2
(a + b)(a - b) = 16
a - b = 16 / (a + b)
Решим систему уравнений:
a + b = 20
a - b = 16 / (a + b) (2)
Решая систему уравнений (1) и (2), найдем:
a = 12 см
b = 8 см
Таким образом, длина основания трапеции равна 12 см.
Пример 2:
Известны длина средней линии трапеции и обе ее диагонали. Найдем длину основания трапеции.
Дано:
Средняя линия = 9 см
Диагональ 1 = 6 см
Диагональ 2 = 4 см
Решение:
Пусть основания трапеции равны a и b, а средняя линия равна м.
Используя свойства трапеции, мы можем записать следующие формулы:
a + b = 2м (1)
С помощью теоремы Пифагора, мы можем записать:
a^2 - b^2 = 6^2 - 4^2
(a + b)(a - b) = 20
a - b = 20 / (a + b) (2)
Решим систему уравнений:
a + b = 18
a - b = 20 / (a + b) (3)
Решая систему уравнений (1) и (3), найдем:
a = 10 см
b = 8 см
Таким образом, длина основания трапеции равна 10 см.
Примеры решений задач помогут вам лучше понять, как применять указанный калькулятор и быстро находить основание трапеции по средней линии и диагонали.