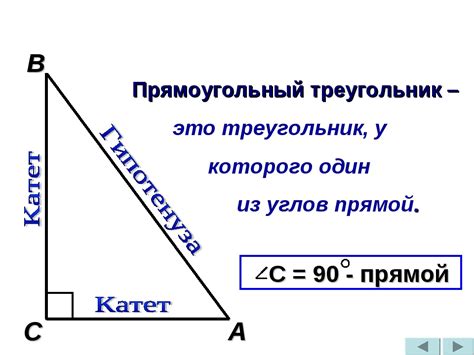
Прямоугольный треугольник – это такой треугольник, у которого один из углов является прямым (равным 90 градусам). При изучении геометрии на практике часто возникает вопрос о нахождении неизвестной стороны прямоугольного треугольника, имея известные другие стороны. В этой статье мы рассмотрим, как найти второй катет прямоугольного треугольника, если известен первый катет.
Первый катет – это одна из сторон прямоугольного треугольника, примыкающая к прямому углу. Обозначается она буквой a. Если известен первый катет и один из других элементов прямоугольного треугольника, то можно простым математическим способом вычислить второй катет.
Для нахождения второго катета прямоугольного треугольника можно воспользоваться теоремой Пифагора. Согласно этой теореме, сумма квадратов катетов треугольника равна квадрату его гипотенузы. Таким образом, для нахождения второго катета нам понадобится формула:
Определение понятий

Катет – это одна из сторон прямоугольного треугольника, примыкающая к прямому углу. Он обозначается буквой a или b.
Гипотенуза – это сторона прямоугольного треугольника, лежащая напротив прямого угла. Она обозначается буквой c.
Для нахождения второго катета прямоугольного треугольника, когда известен первый катет и гипотенуза, можно использовать теорему Пифагора: a2 + b2 = c2. Применяя эту теорему, можно выразить второй катет, а затем вычислить его значение.
Прямоугольный треугольник

Для вычисления второго катета прямоугольного треугольника, если известен первый катет, можно использовать теорему Пифагора. Теорема Пифагора утверждает, что квадрат гипотенузы равен сумме квадратов катетов.
То есть, если известна гипотенуза и один из катетов, то можно найти второй катет зная следующую формулу:
Второй катет = √(гипотенуза² - первый катет²)
Таким образом, для вычисления второго катета прямоугольного треугольника, сначала нужно найти квадрат гипотенузы и квадрат первого катета, затем вычесть квадрат первого катета из квадрата гипотенузы и извлечь корень из полученной разности.
Катет
В прямоугольном треугольнике с одним из катетов известным, можно найти второй катет с помощью теоремы Пифагора или пропорции.
Теорема Пифагора устанавливает следующее соотношение: квадрат гипотенузы равен сумме квадратов катетов.
Для нахождения второго катета с использованием пропорции, необходимо знать соотношение длин катетов в прямоугольном треугольнике.
- Для прямоугольного треугольника со сторонами a, b и гипотенузой c, пропорция будет следующей: a/b = b/c, b/a = a/c.
- Если известны длины катета (a) и гипотенузы (c), второй катет (b) можно найти, используя соотношение: b = (a * c) / sqrt(a^2 + c^2).
- Если известны длины катета (b) и гипотенузы (c), второй катет (a) можно найти, используя соотношение: a = (b * c) / sqrt(b^2 + c^2).
Эти методы позволяют находить второй катет прямоугольного треугольника с известным первым катетом.
Теорема Пифагора

Формулировка теоремы: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Если длины катетов обозначить как a и b, а длину гипотенузы – как c, то теорема запишется следующим образом:
a^2 + b^2 = c^2
Теорема Пифагора является основой для многих вычислений в геометрии, физике и инженерии. Она позволяет находить любую из сторон прямоугольного треугольника, если известны две другие стороны.
Формула вычисления второго катета
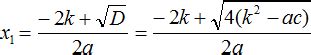
Для вычисления второго катета прямоугольного треугольника, если известен первый катет и гипотенуза, можно использовать теорему Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов:
гипотенуза² = первый катет² + второй катет²
Выражая из этой формулы второй катет:
второй катет = √(гипотенуза² - первый катет²)
Эта формула позволяет находить значение второго катета при заданных значениях первого катета и гипотенузы прямоугольного треугольника. Применение этой формулы может быть полезно при решении геометрических задач или вычислениях в соответствующих областях науки и техники.
Известные данные

Для того чтобы найти второй катет прямоугольного треугольника, необходимо знать следующие данные:
- Длину первого катета, обозначим его как a;
- Значение гипотенузы треугольника, обозначим его как c.
Зная значения этих двух сторон треугольника, можно использовать формулу для нахождения второго катета:
b = √(c^2 - a^2)
где b - длина второго катета.
Применение формулы

Для нахождения второго катета прямоугольного треугольника с известным первым катетом, можно воспользоваться формулой Пифагора:
Второй катет = √(гипотенуза² - первый катет²)
Для простоты вычислений, рекомендуется использовать теорему Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов катетов:
гипотенуза² = первый катет² + второй катет²
Следовательно:
второй катет² = гипотенуза² - первый катет²
И после извлечения квадратного корня, получим значение второго катета.
Геометрическое представление
Прямоугольный треугольник представляет собой треугольник, у которого один из углов равен 90 градусам. Угол, напротив гипотенузы (стороны, противоположенной прямому углу), обозначается как α, а угол, образованный первым катетом и гипотенузой, обозначается как β. В данной задаче известно, что первый катет равен a, а угол α равен 90 градусам.
Для нахождения второго катета b с использованием синуса угла β можно воспользоваться следующей формулой:
где sin β = b / a.
Далее, можно решить уравнение относительно b и получить следующую формулу:
b = a * sin β
Таким образом, угол β и длина первого катета a позволяют найти длину второго катета b с использованием синуса.
Решение примеров

Для решения примеров, где нужно найти второй катет прямоугольного треугольника, с известным первым катетом, можно использовать теорему Пифагора.
Теорема Пифагора гласит:
- В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
- Формула теоремы: a^2 + b^2 = c^2
- Где a и b - катеты, а c - гипотенуза треугольника.
Чтобы найти второй катет, необходимо воспользоваться формулой.
Пример 1:
Известно, что первый катет треугольника равен 3, а гипотенуза равна 5.
Подставляем значения в формулу:
3^2 + b^2 = 5^2
9 + b^2 = 25
b^2 = 25 - 9
b^2 = 16
b = 4
Второй катет треугольника равен 4.
Пример 2:
Известно, что первый катет треугольника равен 6, а гипотенуза равна 10.
Подставляем значения в формулу:
6^2 + b^2 = 10^2
36 + b^2 = 100
b^2 = 100 - 36
b^2 = 64
b = 8
Второй катет треугольника равен 8.
Таким образом, используя теорему Пифагора, можно найти второй катет прямоугольного треугольника при известном первом катете.
Единственность решения

Для прямоугольного треугольника с известным первым катетом существует единственное решение для второго катета. Это связано с особенностями геометрии прямоугольного треугольника.
Первый катет является одной из сторон прямоугольного треугольника, а второй катет - второй стороной. При заданной длине первого катета и правильном построении треугольника, второй катет будет иметь определенную длину, которую можно вычислить с помощью теоремы Пифагора или условий подобия треугольников.
Используя известные значения первого катета, гипотенузы и угла между ними, можно однозначно определить длину второго катета. Второй катет будет всегда меньше гипотенузы и больше первого катета. Это доказывает, что решение для второго катета прямоугольного треугольника с заданным первым катетом существует и является единственным.
