В геометрии существует множество задач, связанных с окружностями и углами. Одной из таких задач является поиск дуги окружности с вписанным углом. В данной статье мы рассмотрим основные правила и алгоритмы, которые помогут вам решить эту задачу.
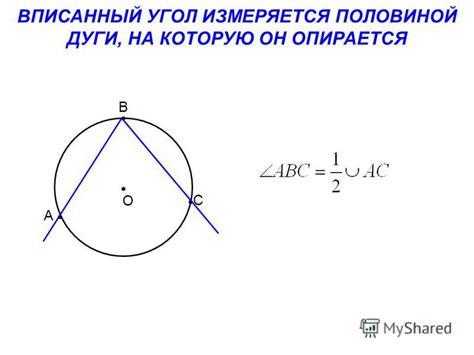
Давайте сначала разберемся, что такое дуга окружности с вписанным углом. В круге или окружности есть много различных углов. Один из них называется вписанным углом. Он образуется двумя хордами, начало и конец которых лежат на окружности. Вписанный угол определяется как угол между этими хордами на окружности.
Чтобы найти дугу окружности с вписанным углом, необходимо знать значения угла, а также радиус окружности. Для решения этой задачи можно использовать несколько алгоритмов. Один из них основан на формуле пересчета дуги окружности в градусы. Другой алгоритм позволяет найти длину дуги окружности, используя радиус и вписанный угол.
Окружность с вписанным углом: основные понятия
Чтобы понять основные понятия, связанные с окружностью с вписанным углом, нужно знать следующие определения:
- Окружность – это множество всех точек на плоскости, которые находятся на одинаковом расстоянии от определенной фиксированной точки, называемой центром окружности.
- Хорда – это отрезок, соединяющий две точки на окружности.
- Радиус – это отрезок, соединяющий центр окружности с любой точкой на этой окружности.
- Диаметр – это хорда, проходящая через центр окружности.
- Угол – это фигура, образованная двумя лучами, исходящими из общей точки.
- Вершина угла – это точка, в которой сходятся два луча, образующих угол.
Познакомившись с этими понятиями, можно более глубоко изучать свойства и алгоритмы работы с окружностью с вписанным углом. На основе этих понятий можно рассчитать длину хорды и угла, найти центр окружности и многое другое.
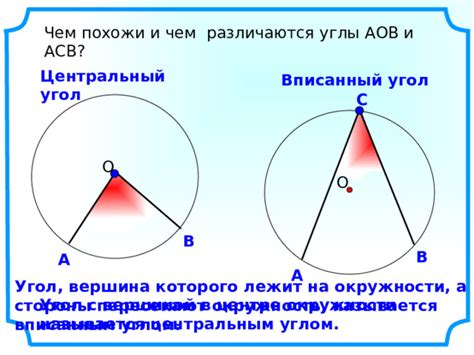
Что такое вписанный угол?

В мире геометрии особое место занимают вписанные углы. Они возникают, когда две или более названные точки пересекают окружность и образуют угол между собой.
Вписанный угол является частью окружности и измеряется по дуге, которую он охватывает. Важно понимать, что вписанные углы, образованные на одной и той же дуге, имеют одинаковые величины. То есть, если на окружности даны две точки и старая точка лежит между новыми точками, то она образует два вписанных угла, которые будут иметь одинаковую меру.
Вписанные углы широко используются в геометрических рассуждениях и доказательствах. Они также имеют важное значение в различных областях науки и техники, в том числе в архитектуре, физике и инженерии.
Что такое окружность с вписанным углом?

Окружность с вписанным углом имеет много интересных свойств и применений. Она используется в геометрии, астрономии, инженерии и других науках. Окружность с вписанным углом является основой для построения многих других геометрических фигур, таких как треугольники, четырехугольники, многоугольники и другие.
Для окружности с вписанным углом существуют специальные правила и алгоритмы, которые позволяют находить дугу окружности, соответствующую заданному углу и его сторонам. Эти правила и алгоритмы основаны на свойствах окружности, таких как радиус, длина дуги, центральный угол и другие.
Окружность с вписанным углом играет важную роль в геометрии и имеет множество применений. Она помогает решать различные задачи, связанные с нахождением длины дуги, площади сектора, углов между сторонами угла и другие. Знание основных правил и алгоритмов по работе с окружностью с вписанным углом является необходимым для успешного решения задач и применения геометрии в практических задачах.
| Правила и алгоритмы для окружности с вписанным углом: |
|---|
| 1. Формула длины дуги окружности: L = r * α |
| 2. Формула площади сектора окружности: S = (r² * α) / 2 |
| 3. Формула центрального угла: α = L / r |
| 4. Формула радиуса: r = L / α |
Эти правила и алгоритмы позволяют находить значения длины дуги, площади сектора, центрального угла и радиуса окружности, основываясь на информации о вписанном угле и его сторонах.
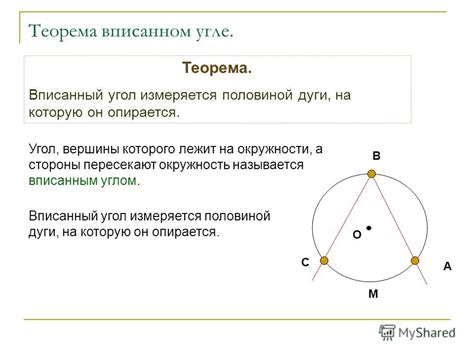
Правила нахождения дуги окружности с вписанным углом
Для начала, необходимо знать значение вписанного угла. Вписанный угол - это угол, который опирается на дугу окружности и имеет свои вершины на этой дуге. Он может быть выражен как в градусах, так и в радианах.
Правило 1: Для нахождения дуги окружности с вписанным углом в градусах, необходимо умножить величину угла на радиус окружности и на π/180. Таким образом, длина дуги окружности (в градусах) равна l = α * r * π/180.
Правило 2: Для нахождения дуги окружности с вписанным углом в радианах, необходимо умножить величину угла на радиус окружности. Таким образом, длина дуги окружности (в радианах) равна l = α * r.
Здесь α - значение включающего угла в градусах или радианах, r - радиус окружности, l - длина дуги окружности.
Также необходимо учитывать, что вписанный угол и длина дуги окружности связаны между собой. Для окружности с радиусом r и вписанным углом α, длина дуги окружности l связана следующим соотношением:
l = 2πr(α/360)
Правило 1: Как найти дугу с вписанным углом, если известна мера самого угла?

В геометрии существует правило, которое позволяет найти дугу окружности с вписанным углом, если известна мера самого угла. Это правило основывается на соотношении между углом и дугой на окружности.
Для того чтобы применить это правило, необходимо знать значение угла. Обозначим это значение буквой α. Затем нужно умножить значение угла на радиус окружности, обозначенный символом R. Полученное произведение будет равно длине дуги, которую мы ищем.
Вычисленная длина дуги будет выражена в радианах, и может быть преобразована в градусы с помощью формулы: длина дуги (в градусах) = (180*длина дуги) / π.
Таким образом, простое умножение значения угла на радиус окружности дает нам длину дуги с вписанным углом. Это правило может быть полезно при решении задач, связанных с вписанными углами и окружностями.
Правило 2: Как найти меру вписанного угла, зная радиус окружности и меру дуги?

Для нахождения меры вписанного угла, зная радиус окружности и меру дуги, мы можем воспользоваться следующей формулой:
| Угол (в радианах) | Угол (в градусах) | Формула |
| θ | θ | θ = L / r |
где:
- θ - мера вписанного угла в радианах или градусах;
- L - мера дуги окружности, которую ограничивает вписанный угол;
- r - радиус окружности.
Чтобы найти меру угла в радианах, достаточно разделить меру дуги на радиус окружности.
Если вам известна мера угла в радианах, вы можете легко перевести ее в градусы, используя следующую формулу:
θ (в градусах) = θ (в радианах) * (180 / π), где π - число Пи (примерно равно 3.14159).
Таким образом, зная радиус окружности и меру дуги, вы можете легко вычислить меру вписанного угла в радианах или градусах.
Алгоритмы нахождения дуги окружности с вписанным углом
- Алгоритм перебора состоит в переборе всех возможных дуг окружности, подходящих под заданный угол. Для каждой дуги вычисляются координаты точек на окружности и проверяется, соответствует ли угол между ними заданному значению. Этот метод может быть достаточно медленным, особенно при большом числе возможных дуг, но он гарантирует точное решение.
- Алгоритм биссектрисы использует геометрическое свойство угла и биссектрису этого угла. Биссектриса угла делит его пополам и проходит через центр окружности. Таким образом, можно найти центр дуги окружности, а затем, зная радиус, найти нужную дугу. Этот метод является более быстрым, так как не требует перебора всех возможных дуг окружности.
- Алгоритм тангенса основан на свойствах тангенса и соотношениях между сторонами прямоугольного треугольника. Зная угол и радиус, можно вычислить сторону треугольника и затем найти дугу окружности, соответствующую данному углу. Этот метод также является быстрым, но может потребовать более сложных вычислений.
Выбор конкретного алгоритма зависит от задачи и доступных ресурсов. Некоторые алгоритмы могут быть более эффективными в вычислительном отношении, однако требуют более сложных вычислений или имеют ограничения. В любом случае, эти алгоритмы играют важную роль в нахождении дуги окружности с вписанным углом и помогают в решении множества задач геометрии.
Алгоритм 1: Как вычислить длину дуги, зная радиус окружности и меру вписанного угла?

1. Найдите длину окружности, используя формулу C = 2πr, где C - длина окружности, π (пи) - математическая константа, равная примерно 3,14159, r - радиус окружности.
2. Вычислите долю от всей окружности, соответствующую вписанному углу, используя формулу L = (m/360) * C, где L - длина дуги, m - мера вписанного угла (в градусах), C - длина окружности.
3. Полученное значение L будет являться искомой длиной дуги окружности.
| Пример: | Результат: |
|---|---|
| Радиус окружности (r): 5 | Длина дуги окружности (L): ... |
| Мера вписанного угла (m): 45° |
Вычисление длины дуги окружности с помощью данного алгоритма позволяет получить точное значение длины, основанное на математических расчетах.