Окружности и их свойства являются одной из основ геометрии. Они применяются в различных научных и технических областях, а также используются в повседневной жизни. Одним из важных понятий окружности является хорда - отрезок, соединяющий две точки на окружности.
Часто при решении задач возникает необходимость найти площадь или длину части окружности, ограниченной заданной хордой. Существует несколько способов решения данной задачи, однако мы предлагаем вам использовать простой способ, основанный на геометрических свойствах окружности.
Для начала определим некоторые понятия. Пусть S - площадь треугольника, образованного хордой и радиусом, проведенным к ее концам. Тогда, в соответствии с геометрическими свойствами окружности, площадь сектора окружности, ограниченного этой хордой, равна произведению площади треугольника S на 2π.
Предлагаем следующую формулу для вычисления площади сектора S:
S = r^2 * α / 2,
где r - радиус окружности, α - центральный угол, отсчитывающийся от хорды до линии, соединяющей центр окружности с одним из концов хорды.
Таким образом, используя данную формулу, вы сможете легко найти площадь части окружности, ограниченной заданной хордой. Успехов вам в решении геометрических задач!
Как найти часть окружности
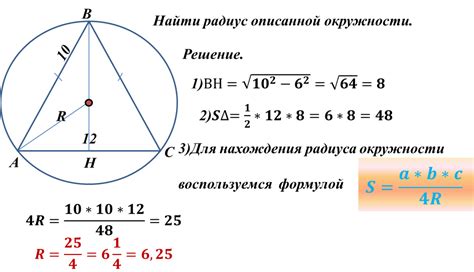
Если известны длина хорды (l) и радиус окружности (r), то площадь сегмента можно найти по следующей формуле:
S = r^2 * arccos(1 - l/r) - (l * sqrt(2rl - l^2)) / 2
Где:
S - площадь сегмента;
r - радиус окружности;
l - длина хорды;
arccos - арккосинус (обратная функция косинуса);
sqrt - квадратный корень.
Эта формула позволяет найти не только площадь сегмента, но и другие параметры, такие как длина дуги или высота сегмента. Она основана на геометрических свойствах окружности и хорды, и может быть использована для решения различных задач в геометрии и математике.
Определение хорды

Важно отметить, что хорда не обязательно проходит через центр окружности. Также, хорда в окружности может быть равна диаметру - длине отрезка, соединяющего две противоположные точки на окружности.
Зная длину хорды и радиус окружности, можно вычислить другие параметры окружности, такие как длина дуги и площадь сектора, используя различные математические формулы.
Важно помнить, что при решении задач на поиск части окружности по заданной хорде, необходимо знать длину хорды, а также радиус окружности. В противном случае, задача может быть неразрешимой.
Свойства хорды
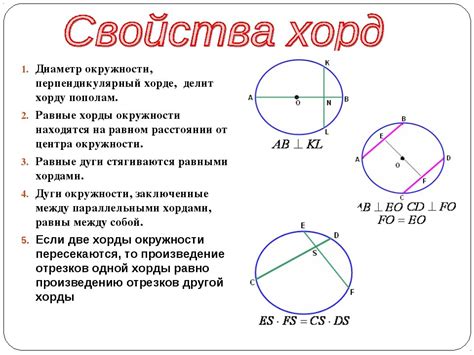
1. Длина хорды равна расстоянию между двумя точками на окружности, которые она соединяет.
2. Если в окружности провести диаметр (отрезок, проходящий через центр окружности и соединяющий две точки на ее окружности), то хорда, перпендикулярная к диаметру, будет являться диаметральной хордой. Диаметральная хорда делит окружность на две равные полуокружности.
3. В окружности, все хорды, имеющие одну и ту же длину, расположены на одинаковом расстоянии от центра окружности.
4. Хорда, пересекающая диаметральную хорду и не проходящая через центр окружности, называется неправильной хордой. Неправильная хорда делит окружность на две неравные полуокружности.
5. Если в окружности провести хорду и перпендикуляр к ней через центр окружности, то он будет проходить через середину хорды.
Свойства хорды полезны при решении задач, связанных с нахождением части окружности по заданной хорде. Зная длину хорды и применяя геометрические законы, можно определить другие параметры окружности, например, радиус или длину дуги.
Построение окружности по хорде
Построение окружности по заданной хорде одним из самых простых способов осуществляется с использованием циркуля и линейки.
Для начала, необходимо взять циркуль и нарисовать две перпендикулярные прямые, пересекающиеся в точке. Это точка будет центром окружности. Далее, проведя линию, проходящую через середину хорды и центр окружности, получим радиус окружности.
При необходимости определить длину хорды или углы, можно провести меридиан, пересекающий хорду под прямым углом. Также можно использовать специальные формулы для вычисления радиуса, радиуса-вектора или дуги окружности.
Построение окружности по хорде весьма просто и доступно даже без специальных математических знаний. Главное - правильно использовать циркуль и линейку, а также найти середину хорды и провести линию через нее и центр окружности.
Вычисление радиуса окружности
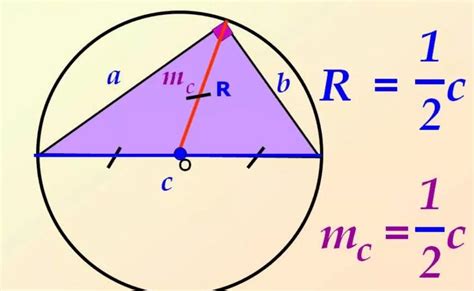
Для вычисления радиуса окружности по заданной хорде необходимо применить следующую формулу:
r = h2 / (8 * a) + a / 2,
где r - радиус окружности, h - длина хорды, a - расстояние от центра окружности до хорды (высота, опущенная на хорду).
Для начала необходимо вычислить длину хорды h и расстояние от центра окружности до хорды a.
Затем, подставляя значения h и a в формулу, необходимо произвести вычисления и получить значение радиуса окружности r.
Пример:
Дано: длина хорды h = 8 и расстояние от центра окружности до хорды a = 4.
Вычисления:
Подставляем значения в формулу: r = 82 / (8 * 4) + 4 / 2 = 64 / 32 + 2 = 4 + 2 = 6.
Ответ: радиус окружности r = 6.
Таким образом, мы нашли радиус окружности по заданной хорде и расстоянию от центра окружности до хорды.
Вычисление площади сегмента окружности
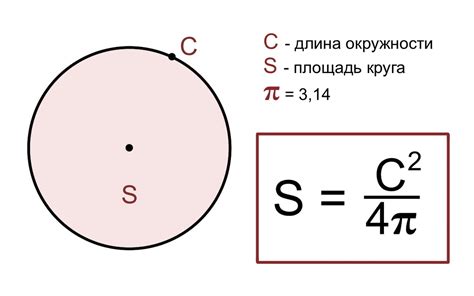
Площадь сегмента окружности можно вычислить с использованием формулы, основанной на радиусе окружности и центральном угле, определяющем сегмент.
Формула для вычисления площади сегмента окружности:
- Шаг 1: Найти длину секущей, которая является хордой сегмента.
- Шаг 2: Найти центральный угол, соответствующий сегменту окружности.
- Шаг 3: Вычислить площадь сегмента окружности, используя формулу:
S = (r²/2) * (θ - sinθ), где S - площадь сегмента, r - радиус окружности, θ - центральный угол в радианах.
Таким образом, зная радиус окружности и центральный угол, можно легко вычислить площадь сегмента окружности с помощью данной формулы.
Например, если у нас есть окружность с радиусом r = 5 и центральным углом θ = π/3 (60 градусов), мы можем вычислить площадь сегмента окружности следующим образом:
S = (5²/2) * (π/3 - sin(π/3)) = (25/2) * (π/3 - √3/2) ≈ 6.794
Таким образом, площадь сегмента окружности составляет примерно 6.794 квадратных единиц, при условии заданных параметров.