Изучение квадратичных функций является важной частью программы школьного курса математики. Однако, когда ученику дают график, а его просят найти соответствующую функцию, это может вызвать затруднения. В этой статье мы рассмотрим подробную презентацию о том, как найти коэффициенты квадратичной функции по графику.

Прежде чем начать, давайте восстановим определение квадратичной функции. Квадратичная функция - это функция вида f(x) = ax^2 + bx + c, где a, b и c - это коэффициенты, а x - это переменная. Коэффициент a называется ведущим коэффициентом и определяет выпуклость (a > 0) или вогнутость (a

Чтобы найти коэффициенты квадратичной функции по графику, вам понадобится несколько точек этого графика. Лучше всего использовать точки, в которых значение x равно 0, 1 и -1, так как это наиболее простые значения для вычислений. Подставляя эти значения в функцию и используя координаты соответствующих точек, мы сможем составить систему уравнений и найти значения коэффициентов a, b и c.

Как определить коэффициенты квадратичной функции по графику

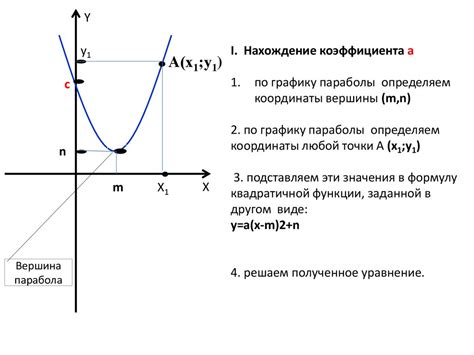
Коэффициенты квадратичной функции могут быть определены по графику этой функции. Квадратичная функция имеет общий вид:

y = ax^2 + bx + c

где y - значение функции, x - переменная, a, b и c - коэффициенты

Для определения коэффициентов квадратичной функции по графику, необходимо иметь как минимум три точки на графике. Чем больше точек, тем точнее будет результат.

Во-первых, найдите вершину параболы. Вершина параболы - это точка, в которой значение функции достигает максимума или минимума. Она имеет координаты (h, k), где h - это x-координата вершины, а k - это y-координата вершины.

Зная координаты вершины, вы можете найти значение a по формуле a = k.

Затем, используя вершину параболы, найдите еще две точки на графике. Лучше всего выбирать точки, которые лежат на одинаковом расстоянии от вершины параболы.

Подставьте координаты этих двух точек в уравнение квадратичной функции и решите систему уравнений относительно b и c. После решения системы, вы сможете найти значения b и c.

Если у вас есть больше точек, то лучше провести аппроксимацию методом наименьших квадратов. Этот метод позволяет найти наилучшую параболу, проходящую через заданные точки.

Итак, если у вас есть график квадратичной функции и вы хотите определить ее коэффициенты, следуйте вышеуказанным шагам.

Метод наименьших квадратов

Основная идея метода заключается в том, чтобы построить модель функции, которая приближается к графику с минимальной погрешностью. Для этого необходимо определить квадратичную функцию вида:

f(x) = ax^2 + bx + c

где a, b и c - коэффициенты, которые необходимо найти.

Затем, используя данные о значениях функции на графике, можно составить систему уравнений, которая связывает значения функции с известными значениями аргумента. Эта система уравнений может быть решена методом Гаусса или любым другим методом решения системы уравнений.

Нахождение коэффициентов квадратичной функции по графику позволяет аппроксимировать функцию и использовать ее для прогнозирования значений функции вне заданного диапазона. Также этот метод может быть использован для анализа и интерпретации данных, полученных в экспериментах или наблюдениях.

Метод наименьших квадратов является эффективным и универсальным инструментом для оценки коэффициентов квадратичной функции по графику. Он позволяет получить точные и надежные значения коэффициентов, учитывая погрешность измерений и шум на графике.

Определение вершины параболы

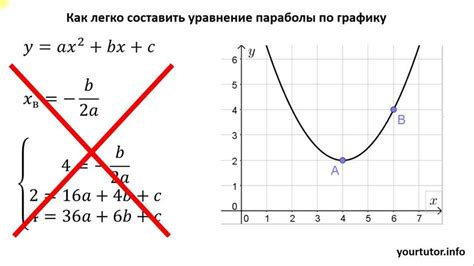
Чтобы определить координаты вершины параболы, можно воспользоваться различными способами:

1. Метод завершения квадратного трехчлена. Если квадратичная функция дана в виде уравнения y = ax^2 + bx + c, то координаты вершины можно найти по формулам: x = -b/2a и y = f(x). Здесь f(x) - это значение функции при заданном x.
2. Анализ графика. Если у нас уже есть график функции, вершина параболы можно определить, просто изучив его внешний вид. Вершина будет представлена в виде точки на графике, где функция достигает своего максимального значения (вершина параболы вниз) или минимального значения (вершина параболы вверх).

Определение вершины параболы очень важно при анализе функции и ее графика, так как оно позволяет определить направление выпуклости/вогнутости параболы, а также точку, в которой она достигает своего экстремального значения.

Расстояние от вершины до точек графика

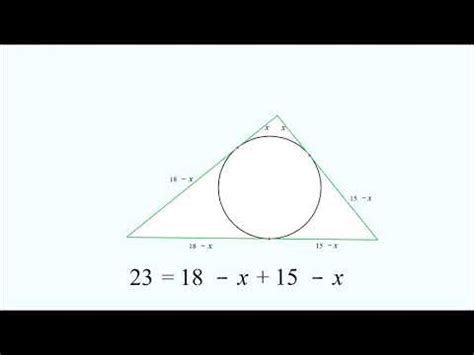
Расстояние от вершины квадратичной функции до точек ее графика можно вычислить с помощью формулы.

Для квадратичной функции вида y = ax^2 + bx + c, вершина графика будет находиться в точке с координатами (h, k), где:

• h - координата вершины по оси x
• k - координата вершины по оси y

Получив координаты вершины, можно вычислить расстояние от вершины до точек графика, используя формулу:

d = |y - k|

Где:

• d - расстояние от вершины до точки графика
• y - значение функции в точке графика
• k - значение функции в вершине графика

Таким образом, чтобы найти расстояние от вершины до точек графика, необходимо подставить значения функции в формулу и вычислить разность между значением функции в точке графика и значением функции в вершине.

Вычисление коэффициентов квадратичной функции

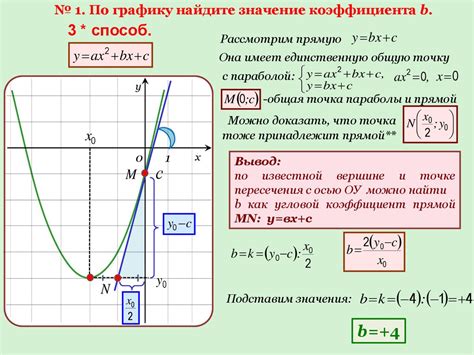
Начнем с определения квадратичной функции в общем виде: y = ax^2 + bx + c, где a, b и c - это коэффициенты, которые требуется найти. Важно отметить, что коэффициент a не равен нулю, иначе у нас была бы линейная функция.

Первым шагом в процессе нахождения коэффициентов является определение вершины параболы. Вершина имеет координаты (h, k), где h = -b / (2a) и k = f(h), где f(h) - значение функции в точке h.

Далее, для определения коэффициента c, можно использовать найденные координаты вершины и подставить их в исходную функцию: c = f(0) - ah^2 - bh.

Также можно найти две дополнительные точки на графике, через которые проходит парабола. Например, если у нас есть точка (x1, y1), мы можем использовать ее координаты, чтобы составить систему уравнений и найти значения a и b.

Система уравнений будет выглядеть следующим образом:

Решая эту систему уравнений, мы можем найти значения для a и b. После того, как все значения найдены, мы можем записать квадратичную функцию в виде уравнения с уже известными коэффициентами.

Таким образом, для вычисления коэффициентов квадратичной функции требуется определить вершину параболы, использовать ее координаты для нахождения коэффициента c и найти дополнительные точки на графике для системы уравнений, чтобы найти значения a и b.