Сетевой график - это мощный инструмент для планирования и управления проектами. Одним из важных аспектов анализа сетевых графиков является определение критического пути, который влияет на общую продолжительность проекта. Критический путь представляет собой последовательность активностей, которая определяет минимальное время выполнения всего проекта.
В этой статье мы рассмотрим, как найти критический путь в сетевом графике с помощью метода наименьших затрат (МНЗ) и алгоритма Л.Ф. Магнина. Первый шаг - построение сетевого графика, включающего список активностей и их продолжительность. После этого мы используем МНЗ для определения ранних и поздних сроков начала и окончания каждой активности.
После определения ранних и поздних сроков мы можем вычислить полный путь проекта, который представляет собой последовательность активностей, на которых достигаются поздние сроки окончания. Пути, которые имеют одинаковые ранние и поздние сроки, являются критическими путями. Они определяют минимальное время выполнения проекта и на них следует сконцентрировать внимание в процессе управления проектом.
Важно отметить, что критический путь может изменяться по ходу выполнения проекта в зависимости от задержек или ускорений в выполнении активностей. Поэтому регулярное обновление и мониторинг сетевого графика является неотъемлемым компонентом эффективного управления проектом. Критический путь помогает идентифицировать задачи, которые максимально влияют на сроки проекта, и позволяет принимать своевременные меры для минимизации рисков и обеспечения успешного завершения проекта вовремя.
Что такое критический путь?

Критический путь представляет собой последовательность связанных задач, где каждая задача зависит от завершения предыдущей и приводит к началу следующей. Весь проект может быть разделен на несколько параллельных путей, но критический путь будет содержать задачи, которые являются самыми длительными и определяют общее время выполнения проекта.
Критический путь имеет наибольшую длительность и не допускает задержек, так как любая задержка на критическом пути автоматически приведет к задержке всего проекта. Поэтому управление критическим путем является важной задачей для успешной реализации проекта.
Определение критического пути включает в себя оценку продолжительности каждой задачи, определение зависимостей между ними и последующую построение сетевого графика. На основе сетевого графика можно выделить критический путь и рассчитать его общую длительность.
Шаг 1: Постройка сетевого графика
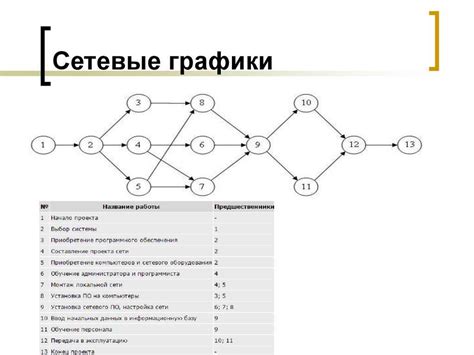
Для начала процесса нахождения критического пути в сетевом графике необходимо построить сам график. Сетевой график представляет собой графическое отображение всех задач, их взаимосвязей и зависимостей друг от друга.
Для построения сетевого графика можно использовать различные методы, такие как методы стрелок, диаграмм Ганта или метод преобразования схемы. В данном случае мы рассмотрим метод стрелок, который является одним из наиболее распространенных и простых в использовании.
Процесс построения сетевого графика с использованием метода стрелок состоит из следующих шагов:
1. Определение всех задач, которые необходимо выполнить для достижении цели проекта.
2. Установление связей и зависимостей между задачами. Необходимо определить, какие задачи являются предшествующими для выполнения других задач, а какие задачи являются последующими.
3. Установление продолжительности каждой задачи. Необходимо определить, сколько времени потребуется для выполнения каждой задачи.
4. Построение сетевого графика по полученным данным. Для этого используются стрелки, которые соединяют задачи между собой в порядке их выполнения.
5. Определение начальной и конечной точки графика. Начальная точка - это задача, с которой начинается проект, а конечная точка - это задача, которая заканчивает проект.
После завершения этих шагов вам будет готов сетевой график проекта, и вы сможете продолжить процесс нахождения критического пути, который будет рассмотрен в следующем шаге.
Анализ и описание задач

Первый шаг в поиске критического пути – это создание сетевого графика, в котором задачи представлены в виде вершин, а связи между задачами – в виде дуг. Каждая задача имеет длительность выполнения, которая отражает время, необходимое для ее завершения.
После создания сетевого графика необходимо провести анализ и определить следующие показатели:
- Ранние начальные и конечные сроки выполнения задач, которые определяются при условии, что все задачи выполняются без задержек и без ожидания ресурсов;
- Поздние начальные и конечные сроки выполнения задач, которые определяются при условии, что все задачи выполняются наиболее позднее время, не нарушая сроки завершения проекта;
- Полный путь, который представляет собой путь от начальной задачи до конечной задачи через задачи с наибольшей общей длительностью выполнения;
- Критический путь, который является частью полного пути и представляет собой последовательность задач, нельзя задерживать без задержки всего проекта.
Анализ критического пути в сетевом графике позволяет выявить задачи, влияющие на сроки выполнения проекта, и принять необходимые меры для их оптимизации. Управление критическим путем позволяет достигнуть более эффективного планирования и выполнения проектов, что способствует улучшению качества и выгодности бизнеса.
Построение диаграммы
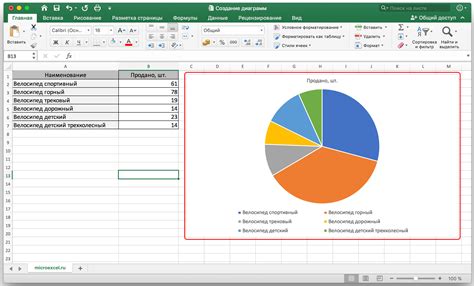
Для начала процесса анализа и определения критического пути в сетевом графике необходимо построить диаграмму, которая позволит наглядно отобразить все задачи, их зависимости и продолжительность выполнения.
Для построения диаграммы используется таблица с двумя столбцами. В первом столбце указываются номера задач, а во втором столбце указывается продолжительность выполнения каждой задачи. Если задачи имеют зависимости, то между ними проводятся стрелки, указывающие направление выполнения задач.
Чтобы определить связи между задачами, можно использовать следующие обозначения:
| Обозначение | Описание |
|---|---|
| – | Нет связи |
| → | Задача должна быть выполнена перед следующей |
| ← | Задача должна быть выполнена после предыдущей |
| ↔ | Задачи могут быть выполнены одновременно |
При построении диаграммы важно учитывать временные затраты на выполнение каждой задачи. Время выполнения задачи обозначается числом во втором столбце диаграммы.
После построения диаграммы можно приступить к определению критического пути и выявлению наиболее критичных задач в сетевом графике.
Шаг 2: Определение длительности задач
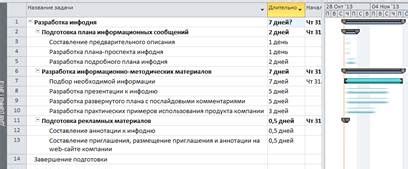
Для определения длительности задачи необходимо учитывать следующие факторы:
- Объем работы: оцените количество работ, которые необходимо выполнить для завершения задачи. Разбейте задачу на более мелкие подзадачи, если это необходимо.
- Ресурсы: учтите наличие ресурсов, необходимых для выполнения задачи, таких как людские ресурсы, материалы или оборудование. Если ресурс ограничен или недоступен, это может повлиять на длительность задачи.
- Опытность исполнителя: учтите опытность исполнителя задачи. Если исполнитель уже имеет опыт в выполнении подобных задач, это может сократить длительность задачи. В противном случае, время на освоение новых навыков и обучение должно учитываться.
- Зависимости: учтите зависимости задачи от других задач. Некоторые задачи могут быть выполнены параллельно, в то время как другие задачи могут зависеть от завершения предыдущих задач, и это может повлиять на длительность задачи.
После учета всех факторов, вы можете определить длительность каждой задачи. Обычно длительность задачи определяется в сетевом графике и указывается в виде числа, помещенного рядом с соответствующей задачей.
Установление преемственности задач

Преемственность задаче в сетевом графике определяется последовательностью выполнения задач и зависимостями между ними. Установление преемственности задач позволяет определить, какие задачи должны быть выполнены до других, чтобы обеспечить успешную реализацию проекта.
Для установления преемственности задач важно провести анализ зависимостей между ними. Зависимости могут быть двух типов:
- Прямая зависимость - задача B может быть выполнена только после выполнения задачи A.
- Обратная зависимость - задача B должна быть выполнена перед выполнением задачи A.
Для удобства анализа зависимостей, можно использовать таблицу сетевого графика, где каждая строка представляет задачу, а столбцы показывают, от каких задач зависит данная задача и на какие задачи она влияет.
Процесс установления преемственности задач включает в себя следующие шаги:
1. Определение начальной и конечной задачи. Начальная задача не зависит от других задач, а конечная задача не имеет зависимостей от других задач.
2. Построение таблицы сетевого графика. В таблице каждая строка соответствует задаче, а столбцы показывают, от каких задач зависит данная задача. В ячейке таблицы можно указать тип зависимости (прямая или обратная).
3. Анализ связей между задачами. На основе таблицы сетевого графика определяются зависимости между задачами и устанавливается последовательность выполнения задач.
В результате установления преемственности задач можно определить критический путь в сетевом графике - последовательность задач, которые необходимо выполнить для завершения проекта в минимальное время.
Установление преемственности задач является важным этапом планирования проекта и позволяет оптимизировать его выполнение, уменьшить риски и повысить эффективность работы.
Оценка времени выполнения задач

При оценке времени выполнения задачи можно использовать различные методы. Наиболее распространенным методом является метод экспертной оценки, при котором опытные специалисты внимательно анализируют каждую задачу и прогнозируют время, необходимое для ее выполнения. При этом учитываются такие факторы, как сложность задачи, ресурсы, доступные для ее выполнения, опыт исполнителей и другие сопутствующие факторы.
Дополнительным инструментом, который можно использовать при оценке времени выполнения задачи, является определение параметров задачи, таких как объем работы, сложность, необходимые ресурсы и другие, и затем применение соответствующих математических моделей для определения временных характеристик задачи.
Важно отметить, что время выполнения задачи может быть разной в зависимости от условий и окружающих факторов. Поэтому при оценке времени выполнения задачи необходимо учесть возможные риски и факторы, которые могут повлиять на выполнение задачи и результаты проекта в целом.
Таким образом, оценка времени выполнения задач играет важную роль при построении сетевого графика проекта и позволяет определить критический путь, а также составить оптимальное расписание работы команды.
Шаг 3: Вычисление ранних и поздних сроков
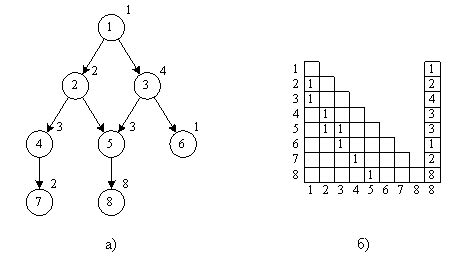
Ранний срок (ES) для каждой задачи - это самая ранняя возможная дата, когда задача может быть выполнена, и зависит от начальных задач в сети.
Поздний срок (LS) для каждой задачи - это самая поздняя возможная дата, когда задача должна быть выполнена, чтобы не задержать завершение проекта. Он определяется относительно конечных задач в сети.
Для вычисления ранних и поздних сроков используется следующая методика:
| Шаг | Описание |
|---|---|
| 1 | Устанавливаем ранний срок (ES) для первой задачи равным 0. |
| 2 | Для каждой последующей задачи, ранний срок (ES) определяется как максимальное значение из ранних сроков (ES) всех предшествующих задач, к которым есть исходящие связи. |
| 3 | Устанавливаем поздний срок (LS) для последней задачи равным раннему сроку (ES) этой задачи. |
| 4 | Для каждой предшествующей задачи, поздний срок (LS) определяется как минимальное значение из поздних сроков (LS) всех последующих задач, к которым есть входящие связи. |
| 5 | Определяем полный резерв времени (TF) каждой задачи как разницу между поздним сроком (LS) и ранним сроком (ES). |
После выполнения всех шагов, мы получим ранние и поздние сроки для каждой задачи, а также полный резерв времени. По этим значениям можно выявить критический путь в сетевом графике - это последовательность задач, на которые нет резерва времени и которые определяют общее время выполнения проекта.