Тригонометрия – это раздел математики, изучающий отношения между сторонами и углами в треугольниках. Одним из важных понятий в тригонометрии является угол, который можно измерить в градусах.
Окружность является особенным случаем треугольника, у которого все три стороны равны. Поэтому в тригонометрии используются специальные понятия и формулы для работы с углами в окружности.
Градусная мера угла – это способ измерения угла, который основан на разделении окружности на 360 равных частей, называемых градусами. Таким образом, полная окружность равна 360 градусам.
Для нахождения градусной меры угла в окружности в тригонометрии используются различные методы и формулы. Например, если дан угол в радианах, чтобы найти его градусную меру, нужно умножить значение угла на 180 и разделить на π.
Угол в окружности
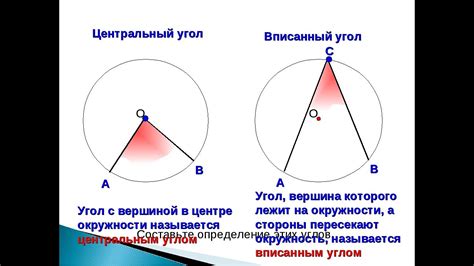
Угол в окружности равный 360 градусам соответствует полной окружности, а каждый градус представляет 1/360 от полного оборота. Таким образом, 180 градусов соответствуют полуокружности, а 90 градусов - четверти окружности.
Угол в окружности может быть измерен как положительным, так и отрицательным числом. Если угол измерен положительно, то он вращается против часовой стрелки, а если отрицательно - то по часовой стрелке.
Важно отметить, что в тригонометрии есть специальные функции, такие как синус, косинус и тангенс, которые связаны с градусной мерой угла в окружности. Эти функции широко используются для решения различных задач, связанных с геометрией и физикой.
Знание о градусной мере угла в окружности является основой для изучения тригонометрии и помогает понять его роль в анализе и моделировании различных явлений и процессов.
Что такое угол в окружности?
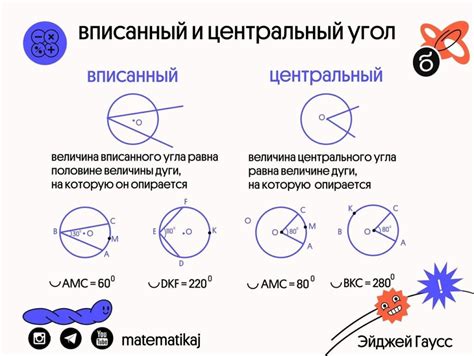
Угловая мера в окружности имеет особое значение в тригонометрии, так как позволяет определить связь между углами и сторонами треугольника, а также осуществлять переходы между градусами и радианами.
Вся окружность составляет угол величиной 360°. Следовательно, любой угол в окружности может быть измерен в градусах от 0° до 360°. Углы, измеряемые в градусах, могут быть положительными или отрицательными, в зависимости от направления вращения лучей.
Углы в окружности имеют много применений, начиная от измерения направления движения и ориентации объектов, заканчивая решением задач геометрии, физики и многих других наук.
Градусная мера угла

Чтобы понять, как найти градусную меру угла в окружности, нужно понимать, что полная окружность имеет 360 градусов. Основываясь на этом, можно вычислить градусную меру для любого угла в окружности.
Методы измерения угла в градусах разработали астрономы в Древней Греции для записи и изучения движения небесных тел. С течением времени градусная мера стала широко использоваться в различных областях, включая тригонометрию.
Для вычисления градусной меры угла на окружности можно использовать соотношение между длиной дуги окружности и радиусом. Также, существуют специальные таблицы значений тригонометрических функций, которые позволяют найти градусную меру угла для различных значений синуса, косинуса и тангенса.
Таким образом, градусная мера угла является важным понятием в тригонометрии и используется для измерения углов в окружности. Это позволяет ученым и инженерам работать с углами и выполнять различные вычисления, связанные с геометрией и физикой.
Формула для расчета градусной меры угла

В тригонометрии градусная мера угла измеряется в градусах. Для расчета градусной меры угла в окружности используется специальная формула.
Предположим, что в радианной мере угол равен α. Чтобы найти градусную меру этого угла, нужно умножить его радианную меру на значение одного градуса в радианах.
Формула для расчета градусной меры угла:
Градусная мера угла = α * (180 / π)
Где:
- Градусная мера угла - результат расчета градусной меры угла
- α - радианная мера угла
- 180 - количество градусов в полном угле
- π (пи) - математическая константа, равная примерно 3.14159
Например, если радианная мера угла равна 1, то градусная мера этого угла будет равна
1 * (180 / π) ≈ 57.2958 градусов.
Таким образом, используя данную формулу, можно легко переводить углы из радианной меры в градусную меру.
Тригонометрические функции угла в окружности
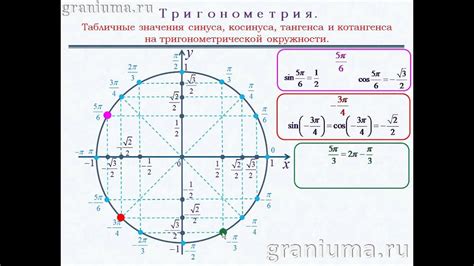
Один из основных углов, с которым мы работаем в тригонометрии, это угол, образованный радиусом и хордой в окружности. Этот угол измеряется в градусах и может быть выражен через тригонометрические функции.
Существует несколько тригонометрических функций, которые связаны с углом в окружности:
- Синус угла (sin): отношение противолежащей стороны к гипотенузе треугольника.
- Косинус угла (cos): отношение прилежащей стороны к гипотенузе треугольника.
- Тангенс угла (tg): отношение синуса угла к косинусу угла.
- Котангенс угла (ctg): отношение косинуса угла к синусу угла.
Эти функции могут быть использованы для решения задач связанных с градусной мерой угла в окружности, например, для нахождения сторон треугольника, если известен угол и одна сторона, или для нахождения угла, если известны две стороны треугольника.
Пример расчета угла в окружности
Представим ситуацию, в которой нам необходимо найти градусную меру угла в окружности. Пусть у нас есть окружность с радиусом 5 см и центром в точке O. Один из сторон угла проходит через центр окружности и образует с положительным направлением оси x угол α.
Чтобы найти градусную меру угла α, мы можем воспользоваться тригонометрическими функциями. Рассмотрим прямоугольный треугольник OAB, где OA - радиус окружности, а AB - сторона треугольника, составляющая угол α с положительным направлением оси x.
Используя определение тригонометрических функций, мы можем записать:
sin α = AB/OA
cos α = OB/OA
Для нашего примера, радиус окружности равен 5 см. Пусть сторона AB треугольника составляет угол α равным 30 градусам. Мы можем использовать эти данные, чтобы найти градусную меру угла α.
Из формул выше, мы можем выразить сторону AB через радиус окружности:
AB = OA * sin α
Подставляя известные значения, получаем:
AB = 5 * sin 30°
Вычисляя sin 30° по таблице значений или с помощью калькулятора, мы получаем:
AB = 5 * 0.5 = 2.5 см
Таким образом, сторона AB треугольника равна 2.5 см. Это означает, что градусная мера угла α в окружности равна 30 градусам.
Таким образом, используя тригонометрию и знания о прямоугольных треугольниках, мы можем легко находить градусную меру угла в окружности.