Модуль Юнга – это одна из важнейших характеристик материала, определяющая его упругие свойства. Она позволяет оценить способность материала изменять свою форму при действии на него механических нагрузок. Расчет модуля Юнга осуществляется с использованием специальной формулы, которую мы рассмотрим далее.
Модуль Юнга обычно обозначается символом E, и он определяется как отношение напряжения к деформации в материале. Иными словами, модуль Юнга показывает, насколько материал упругий и как он ведет себя при деформации.
Для расчета модуля Юнга используется следующая формула:
E = ΔL / (L * ΔS)
Где:
- E - модуль Юнга;
- ΔL - изменение длины материала под действием нагрузки;
- L - исходная длина материала;
- ΔS - изменение площади поперечного сечения материала.
Имея значения изменения длины и площади поперечного сечения материала, можно легко вычислить модуль Юнга. Результатом расчета будет число, выражающееся в Паскалях (Па), то есть в единицах давления.
Что такое модуль Юнга и как его найти
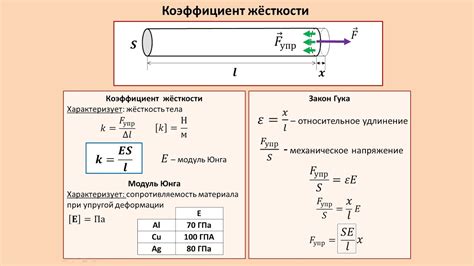
Модуль Юнга обычно обозначается буквой E и измеряется в паскалях (Па) или килопаскалях (кПа). Чтобы найти модуль Юнга, необходимо провести испытание на растяжение или сжатие материала и измерить полученные значения напряжения и деформации.
Формула для расчета модуля Юнга имеет вид:
Где E - модуль Юнга, σ - напряжение (сила деленная на площадь сечения), ε - относительное удлинение (изменение длины под действием силы, деленное на исходную длину).
Испытания на растяжение и сжатие могут проводиться с использованием специального оборудования, такого как растяжной стенд или пресс. Результаты испытаний позволяют определить модуль Юнга и оценить механические свойства материала.
Определение и принцип работы
Принцип работы модуля Юнга основан на измерении деформации материала при приложении к нему некоторых механических напряжений. Для этого на образец материала накладывается одноосное растяжение, и измеряется относительная деформация (изменение длины образца).
Модуль Юнга вычисляется по простой формуле:
E = σ / ε,
где E - модуль Юнга, σ - напряжение, приложенное к материалу, и ε - относительная деформация.
Таким образом, модуль Юнга позволяет оценить, насколько сильно материал будет менять свою форму при воздействии на него механических нагрузок, и является важным параметром при проектировании и расчете конструкций.
Формула и способы расчета модуля Юнга

Существует несколько способов расчета модуля Юнга:
1. Способ, основанный на измерении деформации
Для расчета модуля Юнга методом измерения деформации необходимо знать два параметра: начальную и конечную длины образца материала (L0 и L1) и соответствующие им начальное и конечное значения приложенной силы (F0 и F1).
Модуль Юнга можно рассчитать по следующей формуле:
E = (F1 - F0) / ((L1 - L0) / L0)
2. Способ, основанный на натяжении или сжатии образца
Для расчета модуля Юнга по этому методу необходимо закрепить образец материала между двумя плоскими поверхностями и приложить к нему известную силу. Измерив деформацию, вызванную этой силой, можно рассчитать модуль Юнга с использованием следующей формулы:
E = (F / A) / (ΔL / L0)
где F - приложенная сила, A - площадь поперечного сечения образца, ΔL - изменение его длины, а L0 - начальная длина образца.
Это основные способы расчета модуля Юнга, которые могут быть применены при анализе упругих свойств различных материалов.
Примеры расчетов модуля Юнга

Е = σ/ε
Где:
Е – модуль Юнга, показывающий, насколько материал жесток или мягок;
σ – напряжение, возникающее в материале;
ε – относительная деформация, изменение формы и размеров материала под действием внешних сил.
Давайте рассмотрим несколько примеров расчетов модуля Юнга. Предположим, у нас есть стальная проволока диаметром 6 мм, на которую действует сила 100 Н и она удлиняется на 0,5 мм. Чтобы найти модуль Юнга стали, мы можем применить формулу:
| Величина | Значение |
|---|---|
| Диаметр проволоки (d) | 6 мм |
| Площадь поперечного сечения проволоки (A) | π * (d/2)^2 |
| Сила, действующая на проволоку (F) | 100 Н |
| Изменение длины проволоки (ΔL) | 0,5 мм |
| Исходная длина проволоки (L) | 100 м |
Сначала найдем площадь поперечного сечения проволоки:
Площадь поперечного сечения проволоки (A) = π * (6/2)^2 = 28,26 мм^2
Затем найдем относительное удлинение проволоки:
Относительное удлинение (ε) = ΔL / L = 0,5 / 100 = 0,005
Наконец, найдем модуль Юнга:
Модуль Юнга (Е) = σ / ε = F / (A * ε) = 100 / (28,26 * 0,005) ≈ 70792 МПа
Таким образом, модуль Юнга стали составляет примерно 70792 МПа.
Иногда модуль Юнга можно найти путем испытания образцов материала. Например, для алюминиевого образца получены следующие значения:
| Величина | Значение |
|---|---|
| Напряжение при разрыве (σ) | 500 МПа |
| Относительное удлинение при разрыве (ε) | 0,04 |
Тогда модуль Юнга можно расчитать по формуле:
Модуль Юнга (Е) = σ / ε = 500 / 0,04 = 12500 МПа
Таким образом, модуль Юнга алюминия составляет 12500 МПа.
Примеры расчетов модуля Юнга демонстрируют использование формулы и важность его определения для анализа механических свойств материалов.
Практическое применение модуля Юнга

Одним из практических применений модуля Юнга является проектирование и расчет конструкций. Зная модуль Юнга материала, инженеры могут определить, как будет деформироваться конструкция под действием нагрузки и предупредить возможные повреждения или разрушение.
Модуль Юнга также используется при выборе и разработке материалов для производства изделий. Зная модуль Юнга материала, можно выбрать подходящий материал с нужными упругими свойствами для конкретной цели. Например, при проектировании пружины необходимо выбрать материал с высоким значением модуля Юнга, чтобы пружина могла эффективно восстанавливать свою форму после сжатия или растяжения.
Необходимость знания модуля Юнга возникает и в области материаловедения. Исследователи используют эту характеристику для изучения свойств различных материалов, а также для сравнения их механической прочности и упругости.
В целом, модуль Юнга является важным понятием в механике и материаловедении. Его практическое применение позволяет инженерам и исследователям эффективно выбирать и использовать материалы, а также предсказывать и предупреждать различные негативные явления, связанные с деформацией и повреждением материалов.
