Окружности – геометрические фигуры, которые могут вызвать путаницу при определении, находится ли точка внутри или снаружи их границ. Физические законы, лежащие в основе этой формы, делают задачу еще более сложной, требуя определенных математических методов для достижения правильных результатов.
Существует несколько простых способов определения наличия точки внутри окружности. Один из них основан на применении пирамиды, восстановленной по трем точкам окружности. Если рассматриваемая точка находится внутри этой пирамиды, то она также будет находиться внутри окружности. В противном случае, она будет считаться внешней точкой.
Еще одним методом является определение расстояния между центром окружности и рассматриваемой точкой. Если расстояние меньше радиуса, то точка находится внутри окружности. В противном случае, она будет считаться внешней точкой.
Наличие современных математических программ и алгоритмов позволяет автоматизировать этот процесс и проводить точную проверку принадлежности точки окружности. Примеры реализации этих алгоритмов можно найти в различных языках программирования, таких как C++, Python и JavaScript.
Методы определения наличия точки внутри окружности
Определение наличия точки внутри окружности может быть выполнено с использованием различных методов. Вот несколько из них:
- Метод с использованием расстояния до центра окружности:
- Метод с использованием координат точки и центра окружности:
- Метод с использованием положительности коэффициента наклона прямой:
Чтобы определить, находится ли точка внутри окружности, можно вычислить расстояние от этой точки до центра окружности. Если расстояние меньше радиуса окружности, то точка находится внутри нее. Если расстояние равно радиусу, то точка находится на окружности. Если расстояние больше радиуса, то точка находится вне окружности.
Если известны координаты точки и центра окружности, можно рассчитать расстояние между этими точками. Если расстояние меньше радиуса окружности, то точка находится внутри нее. Если расстояние равно радиусу, то точка находится на окружности. Если расстояние больше радиуса, то точка находится вне окружности.
Если уравнение окружности известно в виде (x-a)^2 + (y-b)^2 = r^2, где (a,b) - координаты центра окружности, r - радиус окружности, а координаты точки (x,y) определены, то можно подставить их в это уравнение. Если уравнение выполняется, то точка находится внутри окружности. Если оно не выполняется, то точка находится вне окружности.
Определить наличие точки внутри окружности несложно, если использовать один из указанных методов. Зная координаты точки и центра окружности, а также радиус, можно легко определить положение точки относительно окружности.
Геометрический подход к определению наличия точки внутри окружности

Определение наличия точки внутри окружности может быть решено с использованием геометрического подхода. Для этого необходимо вычислить расстояние между центром окружности и данной точкой, а затем сравнить его с радиусом окружности.
Для начала, рассмотрим данный вопрос на двумерной плоскости. Пусть у нас есть окружность с заданными координатами центра и радиусом, а также точка с известными координатами. Воспользуемся формулой вычисления расстояния между двумя точками в декартовой системе координат:
Расстояние = √((x2 - x1)2 + (y2 - y1)2)
Где (x1, y1) - координаты центра окружности, (x2, y2) - координаты данной точки.
Вычисляя данное расстояние, можно сравнить его с радиусом окружности. Если расстояние меньше радиуса, то точка находится внутри окружности. Если расстояние равно радиусу, то точка находится на границе окружности. И, наконец, если расстояние больше радиуса, то точка находится вне окружности.
В таблице ниже приведены примеры координат центра окружности и точек, а также результаты проверки на наличие точки внутри окружности:
| Центр окружности | Точка | Результат |
|---|---|---|
| (0, 0) | (1, 1) | Внутри окружности |
| (0, 0) | (2, 2) | Вне окружности |
| (2, 3) | (3, 4) | На границе окружности |
Применяя геометрический подход и вычисляя расстояние между центром окружности и точкой, возможно точно определить наличие точки внутри окружности. Этот подход может быть применен не только на двумерной плоскости, но и в трехмерном пространстве.
Аналитический подход к определению наличия точки внутри окружности
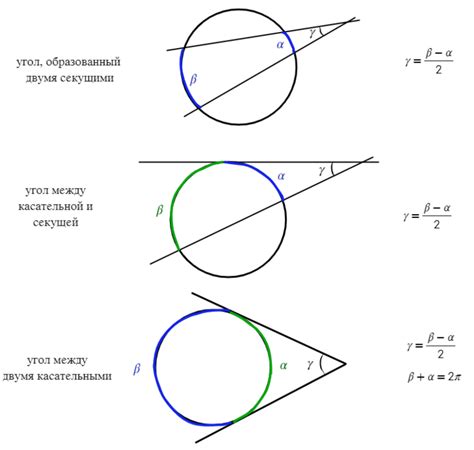
Аналитический подход используется для определения наличия точки внутри окружности с использованием уравнений и координат точек. Для этого необходимо знать координаты центра окружности и ее радиус.
Определять, находится ли точка внутри окружности, можно с помощью следующих условий:
- Рассчитываем расстояние от центра окружности до точки по формуле:
d = sqrt((x - cx)^2 + (y - cy)^2), где (cx, cy) - координаты центра окружности, (x, y) - координаты проверяемой точки. - Сравниваем полученное расстояние с радиусом окружности:
- Если d , где r - радиус, то точка находится внутри окружности.
- Если d = r, то точка лежит на окружности.
- Если d > r, то точка находится вне окружности.
Пример:
Пусть у нас есть окружность с центром в точке (0, 0) и радиусом 5. Необходимо определить, находится ли точка (3, 4) внутри окружности.
Рассчитываем расстояние от центра окружности до точки:
d = sqrt((3 - 0)^2 + (4 - 0)^2) = sqrt(9 + 16) = sqrt(25) = 5
Полученное расстояние равно радиусу окружности, следовательно, точка (3, 4) лежит на окружности.
Таким образом, аналитический подход позволяет точно определить наличие точки внутри окружности или на ее границе по заданным координатам.