Главная » Интересно

Как определить, находится ли точка на окружности? Полезные советы и примеры

На чтение 8 мин Опубликовано Обновлено

Определение, находится ли точка на окружности, является важной задачей в геометрии. Эта информация может быть полезна во многих областях, включая инженерные расчеты, компьютерную графику и разработку игр. В этой статье мы рассмотрим несколько простых способов определения, находится ли точка на окружности, и приведем иллюстративные примеры.

Для определения, находится ли точка на окружности, необходимо учитывать два фактора: координаты центра окружности и радиус окружности. Если известны координаты точки и радиус, можно использовать формулу расстояния между двумя точками на плоскости для определения расстояния от центра окружности до точки. Если полученное расстояние равно радиусу окружности, то точка лежит на окружности.

Кроме того, существует еще один метод для определения, находится ли точка на окружности. Если известны координаты точки и уравнение окружности в канонической форме, можно подставить значения координат точки в уравнение и проверить, выполняется ли оно. Если уравнение истинно, то точка лежит на окружности.

В этой статье мы рассмотрим оба метода и детально их разберем на примерах. Узнаем, какую информацию нужно иметь, чтобы определить, находится ли точка на окружности, и как применять эти знания на практике. Знание этих методов позволит вам более глубоко понять геометрию и использовать ее в различных областях деятельности.

Проверка нахождения точки на окружности: как это сделать правильно

Проверка нахождения точки на окружности: как это сделать правильно
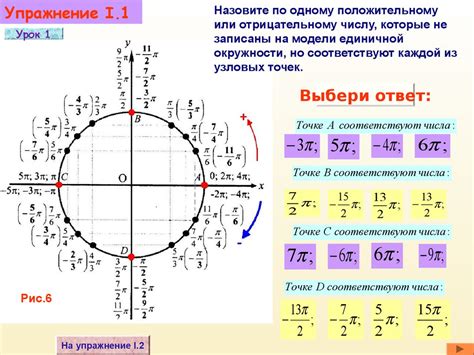
  1. Используя уравнение окружности: чтобы проверить, лежит ли точка на окружности с заданным центром и радиусом, можно подставить координаты точки в уравнение окружности. Если это уравнение истинно, значит точка находится на окружности. В этом случае уравнение окружности имеет вид: (x - a)2 + (y - b)2 = r2, где (a, b) - координаты центра окружности, (x, y) - координаты точки, r - радиус окружности. Если значение левой части равно правой, точка принадлежит окружности.
  2. Используя расстояние от центра до точки: можно проверить, находится ли точка на заданном расстоянии от центра окружности. Если расстояние между центром окружности и точкой равно радиусу, то точка лежит на окружности. Расстояние между двумя точками в плоскости можно определить с помощью формулы: d = sqrt((x2 - x1)2 + (y2 - y1)2), где (x1, y1) - координаты центра окружности, (x2, y2) - координаты точки.
  3. Используя теорему Пифагора: если треугольник, образованный центром окружности, точкой и одной из осей координат, является прямоугольным, то точка находится на окружности. Расстояния между точками на плоскости можно вычислить с помощью теоремы Пифагора: c2 = a2 + b2, где c - гипотенуза, a и b - катеты. В этом случае, если гипотенуза равна радиусу, точка принадлежит окружности.

Определение принадлежности точки к окружности является важным этапом решения геометрических задач. Используйте вышеуказанные методы для проверки нахождения точки на окружности и будьте внимательны при вычислениях.

Основные понятия и формулы

Основные понятия и формулы

Для определения, находится ли точка на окружности, можно использовать следующую формулу:

  • Для окружности с центром в точке C(cx, cy) и радиусом r:
  • Точка P(px, py) находится на окружности, если выполнено следующее равенство:
  • (px - cx)2 + (py - cy)2 = r2

В данной формуле, мы вычисляем квадрат разности между координатами точек и центром окружности. Если сумма этих квадратов равна квадрату радиуса, значит, точка лежит на окружности.

Если полученное значение не равно квадрату радиуса, то точка либо внутри, либо снаружи окружности.

Как найти центр окружности и ее радиус

Как найти центр окружности и ее радиус

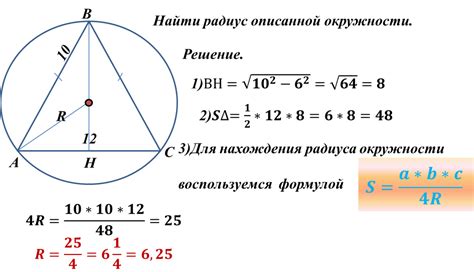
Чтобы найти центр окружности и ее радиус, вам понадобится информация о двух точках, лежащих на окружности. Это может быть любая пара точек на окружности, например, точка пересечения окружности с прямой или точка окружности, заданная углом и расстоянием от начала координат.

Имея информацию о двух точках, вы можете использовать следующие формулы для нахождения центра окружности и ее радиуса:

  1. Найдите середину отрезка, соединяющего две точки. Это будет координаты центра окружности.
  2. Найдите расстояние между центром окружности и одной из точек. Это будет радиус окружности.

Вот пример вычисления центра окружности и ее радиуса с помощью формул:


// Пусть у нас есть две точки на окружности
var точка1 = { x: 3, y: 4 };
var точка2 = { x: -2, y: 1 };
// Найдем координаты центра окружности
var x_центра = (точка1.x + точка2.x) / 2;
var y_центра = (точка1.y + точка2.y) / 2;
// Найдем радиус окружности
var радиус = Math.sqrt((точка2.x - точка1.x) ** 2 + (точка2.y - точка1.y) ** 2) / 2;
// Выведем результаты
console.log('Центр окружности: (' + x_центра + ', ' + y_центра + ')');
console.log('Радиус окружности: ' + радиус);

Теперь вы знаете, как найти центр окружности и ее радиус, используя информацию о двух точках на окружности. Эти знания могут быть полезными при работе с геометрией, программированием или решении задач математики.

Способы определения координат точки

Способы определения координат точки

При работе с окружностями важно уметь определить находится ли точка внутри окружности или на ее границе. Для этого можно использовать различные способы проверки координат точки.

  • Проверка радиуса и расстояния: Для определения, находится ли точка на окружности, можно вычислить расстояние от точки до центра окружности и сравнить его с радиусом. Если расстояние равно радиусу, то точка находится на границе окружности. Если расстояние меньше радиуса, то точка лежит внутри окружности.
  • Проверка уравнения окружности: Можно использовать уравнение окружности для проверки, находится ли точка на окружности. Если подставленные в уравнение координаты точки удовлетворяют его, то точка лежит на окружности.
  • Проверка угла: Если известны координаты центра окружности и координаты точки, то можно вычислить угол между ними. Если угол равен 360 градусов, то точка находится на окружности, иначе - внутри окружности.

Зная эти способы определения координат точки на окружности, вы сможете легко решать задачи, связанные с работой с окружностями.

Проверка нахождения точки на окружности по координатам

Проверка нахождения точки на окружности по координатам

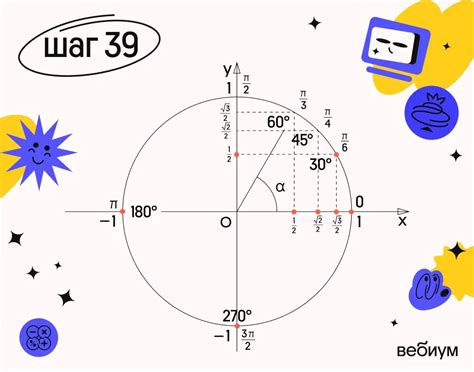
Для определения нахождения точки на окружности с заданными координатами (x, y), необходимо выполнить следующую проверку:

  1. Вычислить расстояние между центром окружности и заданной точкой.
  2. Сравнить полученное расстояние с радиусом окружности.
  3. Если расстояние равно радиусу, то точка находится на окружности.
  4. Если расстояние меньше радиуса, то точка находится внутри окружности.
  5. Если расстояние больше радиуса, то точка находится вне окружности.

Для вычисления расстояния между точками, можно воспользоваться формулой:

расстояние = √((x2 - x1)^2 + (y2 - y1)^2)

Где (x1, y1) - координаты центра окружности, а (x2, y2) - координаты заданной точки.

Пример кода для проверки нахождения точки на окружности:


function isPointOnCircle(x, y, centerX, centerY, radius) {
// Вычисляем расстояние до центра окружности
var distance = Math.sqrt(Math.pow((x - centerX), 2) + Math.pow((y - centerY), 2));
// Сравниваем расстояние с радиусом окружности
if (distance === radius) {
return true;
} else {
return false;
}
}
// Пример использования функции
var pointOnCircle = isPointOnCircle(5, 5, 0, 0, 5);
console.log(pointOnCircle); // true

В данном примере функция isPointOnCircle принимает координаты заданной точки (x, y), координаты центра окружности (centerX, centerY) и радиус окружности (radius). Функция вычисляет расстояние до центра окружности и возвращает true, если расстояние равно радиусу, и false в противном случае.

Примеры задач и решения

Примеры задач и решения

Пример 1:

Даны координаты центра окружности (x0, y0) и ее радиус r. Необходимо определить, находится ли точка с координатами (x, y) на этой окружности или внутри нее.

Решение:

Для определения расстояния между центром окружности и точкой можно использовать теорему Пифагора: sqrt((x - x0)^2 + (y - y0)^2). Если полученное расстояние равно радиусу окружности, то точка лежит на окружности. Если расстояние меньше радиуса, то точка лежит внутри окружности. Иначе точка находится вне окружности.

Пример кода:

function isPointOnCircle(x, y, x0, y0, r) { var distance = Math.sqrt(Math.pow(x - x0, 2) + Math.pow(y - y0, 2)); if (distance === r) { return "Точка лежит на окружности"; } else if (distance < r) { return "Точка лежит внутри окружности"; } else { return "Точка лежит вне окружности"; } } // Пример использования функции var result = isPointOnCircle(3, 4, 0, 0, 5); console.log(result);

Пример 2:

Даны координаты центра окружности (x0, y0) и ее радиус r, а также координаты точки (x, y). Необходимо определить, находится ли точка на окружности, внутри нее или вне нее. В случае, если точка лежит на окружности, также необходимо определить ее расположение: находится ли она на горизонтальном или вертикальном диаметре или на одной из диагоналей окружности.

Решение:

Аналогично предыдущей задаче, мы можем использовать теорему Пифагора для определения расстояния между центром окружности и точкой. Если расстояние равно радиусу окружности, то точка лежит на окружности. Для определения расположения точки на окружности, можно вычислить угол между вектором, соединяющим центр окружности с точкой, и осью X. Если угол равен 0, то точка находится на горизонтальном диаметре, если угол равен 90 градусов - на вертикальном диаметре, если угол равен 45 или 135 градусов - на одной из диагоналей. В противном случае, точка находится где-то между этими линиями.

Пример кода:

function getPointLocation(x, y, x0, y0, r) { var distance = Math.sqrt(Math.pow(x - x0, 2) + Math.pow(y - y0, 2)); var angle = Math.atan2(y - y0, x - x0) * (180 / Math.PI); if (distance === r) { if (angle === 0) { return "Точка лежит на горизонтальном диаметре"; } else if (angle === 90) { return "Точка лежит на вертикальном диаметре"; } else if (angle === 45
Оцените статью