Определение объема тела может показаться сложной задачей, особенно если неизвестна его плотность. Однако существуют простые методы, позволяющие расчитать объем без дополнительной информации. В этой статье мы рассмотрим несколько таких способов, которые помогут вам узнать объем объекта без необходимости знать его плотность.
Первый способ основан на измерении геометрических параметров объекта. Если объект имеет правильную геометрическую форму, то его объем можно расчитать с помощью соответствующих формул. Например, для прямоугольного параллелепипеда объем можно найти, умножив длину, ширину и высоту. Такой метод применим для множества простых геометрических фигур.
Второй способ основан на использовании воды или другой жидкости. Для этого потребуется подходящая емкость, рулетка или линейка, и некоторые простые расчеты. Зная начальный и конечный уровень жидкости в емкости, а также ее объем, можно определить объем объекта. Этот метод особенно полезен при работе с неправильными формами, так как он не требует знания плотности объекта.
Если количество неизвестных веществ небольшое, можно использовать приближенную оценку
Если у вас есть ограниченное количество неизвестных веществ и вы не знаете их плотность, существует простой способ оценки их объема.
Для начала, вам следует измерить массу каждого вещества. Это можно сделать с помощью весов или других средств измерения массы.
Затем, используя измеренные массы и предполагая, что все вещества имеют примерно одинаковую плотность, вы можете сделать приближенную оценку объема каждого вещества. Для этого нужно знать плотность одного известного вещества и использовать его массу вместе с измеренными массами неизвестных веществ.
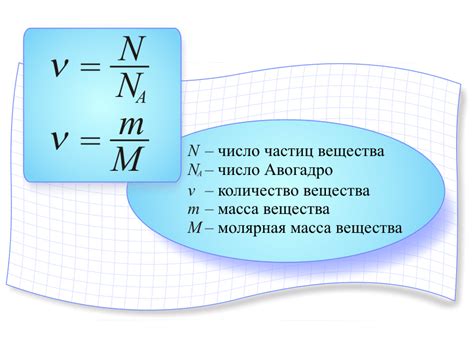
Вы можете использовать следующую формулу для приближенного расчета:
Объем = Масса / Плотность
Например, предположим, что у вас есть три разных вещества с неизвестными плотностями, но вам известна плотность вещества А. Измеренные массы этих веществ составляют 10 г, 15 г и 20 г соответственно. Вы можете использовать плотность вещества А, чтобы оценить их объемы:
- Оценка объема первого вещества: объем = 10 г / Плотность А
- Оценка объема второго вещества: объем = 15 г / Плотность А
- Оценка объема третьего вещества: объем = 20 г / Плотность А
Таким образом, вы можете оценить объем каждого вещества без знания их точной плотности. Однако, стоит помнить, что это лишь приближенные значения и могут быть неточными, особенно если плотности различных веществ отличаются значительно.
Метод сопоставления с известными веществами

Если у вас есть возможность сравнить исследуемый предмет с известными веществами, то можно использовать метод сопоставления. Этот метод основан на принципе равенства объемов у одинаковых предметов.
Однако следует учитывать, что данный метод требует наличия образцов известных веществ с известными плотностями, что не всегда является возможным. Кроме того, допускается погрешность в результате субъективной оценки, поэтому рекомендуется применять этот метод с осторожностью и с учетом всех факторов, которые могут влиять на точность результата.
Несмотря на некоторые ограничения, метод сопоставления с известными веществами может быть полезным инструментом для определения объема без знания плотности, особенно в тех случаях, когда другие методы расчета недоступны или не применимы.
Метод сопоставления с объемом других объектов

Если у вас нет информации о плотности вещества, но вы знаете количество других объектов с известным объемом, то можно воспользоваться методом сопоставления с объемом этих объектов.
Первым шагом необходимо найти объект с похожим объемом и принять его объем в качестве приближенного значения для вашего объекта.
Например, если у вас есть яблоко и вам известен его объем, вы можете найти другое яблоко с похожим объемом или собрать несколько яблок, чтобы получить суммарный объем, известный вам заранее.
Затем, пользуясь этим приближенным значением, вы можете использовать формулу для расчета плотности. Как только плотность известна, вы сможете вычислить искомый объем вашего объекта.
Несмотря на то, что этот метод не точен, он может быть полезным для получения приближенных значений объема без знания плотности. Однако следует учитывать, что результаты могут иметь некоторую погрешность.
Важно отметить, что этот метод работает только в тех случаях, когда у вас есть доступ к объектам с известным объемом для сопоставления. Если такой возможности нет, следует обратиться к другим методам определения объема.
Метод сопоставления с массой вещества

Если у вас нет информации о плотности вещества, но есть возможность определить его массу, можно воспользоваться методом сопоставления с массой.
Для начала, нужно знать массу вещества. Далее, можно воспользоваться информацией о плотности другого вещества, для которого плотность известна.
Шаги для определения объема без знания плотности с использованием метода сопоставления с массой:
- Измерьте массу вещества с помощью весов.
- Выберите вещество с известной плотностью, которое имеет сходные свойства с исследуемым веществом.
- Рассчитайте объем этого вещества, зная его массу и плотность, используя формулу: объем = масса / плотность.
- Сопоставьте полученный объем с объемом исследуемого вещества. Если вещества имеют сходные свойства, то их объемы будут примерно равны.
- Таким образом, можно приближенно определить объем исследуемого вещества.
Важно помнить, что сравнение свойств веществ должно быть как можно более точным, чтобы результат был достаточно точным. Также учтите, что метод сопоставления с массой является приближенным и может давать неточные результаты.
Использование математических формул и уравнений
При отсутствии информации о плотности можно использовать математические формулы и уравнения для определения объема. В зависимости от геометрической формы объекта, на котором необходимо определить объем, можно использовать различные формулы.
Для простых геометрических фигур, таких как куб, прямоугольник или параллелепипед, объем можно вычислить с помощью формулы:
- Объем куба: V = a^3, где a - длина ребра куба.
- Объем прямоугольного параллелепипеда: V = a * b * h, где a, b и h - длины сторон параллелепипеда.
- Объем прямоугольника: V = a * b * c, где a, b и c - длины сторон прямоугольника.
Для более сложных геометрических фигур, таких как сфера, конус или цилиндр, объем можно вычислить с помощью соответствующих формул:
- Объем сферы: V = 4/3 * π * r^3, где π - математическая константа, равная приблизительно 3.14159, а r - радиус сферы.
- Объем конуса: V = 1/3 * π * r^2 * h, где r - радиус основания конуса, а h - высота конуса.
- Объем цилиндра: V = π * r^2 * h, где r - радиус основания цилиндра, а h - высота цилиндра.
Важно помнить, что для применения этих формул необходимо знать значения радиуса, сторон или длин объектов, на которых проводится расчет. Поэтому, при отсутствии информации о плотности, можно использовать описанные формулы для приближенного определения объема.
Метод Геронимуса
Для применения метода Геронимуса необходимо знать длины всех сторон фигуры, объем которой требуется определить. Операция нахождения площади по формуле Герона производится для каждого из слоев фигуры, а затем все полученные площади складываются.
Однако стоит учитывать, что метод Геронимуса подходит только для определенных типов фигур, таких как треугольники, четырехугольники и многоугольники. Для фигур с более сложной формой данный метод может быть не применим.
Метод Геронимуса является достаточно простым в использовании и не требует дополнительных данных, однако его точность зависит от правильного измерения сторон фигуры. Поэтому при использовании метода Геронимуса необходимо быть внимательным при измерении и учитывать погрешности.
Метод аппроксимации
Например, если объект имеет форму прямоугольного параллелепипеда, его объем можно рассчитать как произведение длины, ширины и высоты. Если форма объекта сложнее, например, необычная фигура или неоднородная поверхность, метод аппроксимации может позволить получить приближенное значение объема.
При использовании метода аппроксимации важно помнить, что полученное значение будет лишь приближением, основанным на предположении о форме объекта. Точность такого расчета будет зависеть от точности аппроксимации и соответствия предположенной формы реальной форме объекта.
Для улучшения точности приближенного расчета можно использовать несколько различных аппроксимаций и затем усреднить полученные значения. Такой подход позволяет учесть различные аспекты формы объекта и повысить точность расчета.
Метод аппроксимации является основным приемом расчета объема без знания плотности. Он находит применение в различных областях, включая строительство, геологию и промышленность.