Объем является одним из основных понятий в физике, он позволяет определить, сколько места занимает тот или иной объект. В данной статье мы рассмотрим, как найти объем детали, находящейся в жидкости в призме прямой.
Прежде всего, необходимо знать, что призма – это геометрическое тело, образованное двумя параллельными базами, соединенными боковыми гранями. Обычно призмы имеют тригонометрическую форму, такую как треугольная, прямоугольная или трапециевидная.
Для того чтобы найти объем детали, находящейся в жидкости в призме прямой, необходимо учитывать два параметра – площадь поперечного сечения призмы и высоту уровня жидкости внутри призмы. Площадь поперечного сечения призмы можно найти, зная форму призмы и значения ее сторон.
После того как мы найдем площадь поперечного сечения призмы и высоту уровня жидкости, мы можем использовать формулу для определения объема призмы: V = S x h, где V – объем призмы, S – площадь поперечного сечения, h – высота уровня жидкости.
Как расчитать объем детали в призме
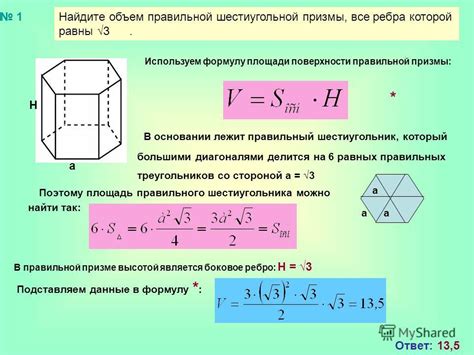
Для расчета объема детали в призме прямой необходимо выполнить несколько простых шагов. В основе расчета лежит формула нахождения объема прямоугольной призмы:
Объем = S * h
Где S - площадь основания призмы, а h - высота призмы.
Чтобы найти площадь основания призмы, необходимо знать геометрическую фигуру основания. Обычно основание призмы представляет собой прямоугольник, треугольник или круг. В зависимости от формы основания будут применяться различные формулы нахождения площади.
Если основание - прямоугольник, то площадь можно найти по формуле:
S = a*b
Где a и b - длины сторон прямоугольника.
Если основание - треугольник, то площадь можно найти по формуле:
S = 1/2 * a * h1
Где a - длина основания треугольника, а h1 - высота треугольника.
Если основание - круг, то площадь можно найти по формуле:
S = π * r^2
Где π - математическая константа, равная приблизительно 3,14, а r - радиус круга.
После нахождения площади основания и высоты призмы, можно легко вычислить объем, умножив эти значения по формуле Объем = S * h. Полученное значение будет являться объемом детали в призме прямой.
Пример:
| Форма основания | Заданные значения | Результат |
|---|---|---|
| Прямоугольник | Длина: 10 см, Ширина: 5 см, Высота: 3 см | Объем: 10 * 5 * 3 = 150 см³ |
| Треугольник | Основание: 6 см, Высота: 4 см, Высота призмы: 8 см | Площадь основания: 1/2 * 6 * 4 = 12 см² Объем: 12 * 8 = 96 см³ |
| Круг | Радиус: 2 см, Высота: 10 см | Площадь основания: 3,14 * 2^2 = 12,56 см² Объем: 12,56 * 10 = 125,6 см³ |
Таким образом, зная форму основания и ее параметры, а также высоту призмы, можно легко расчитать объем детали в призме прямой.
Алгоритм расчета объема детали в призме прямой

Шаг 1: Определите размеры призмы прямой, в которой находится деталь. Измерьте высоту призмы (h), ширину (w) и глубину (d).
Шаг 2: Специфицируйте форму детали, которую вы хотите найти объем. Например, предположим, что деталь имеет форму прямоугольного параллелепипеда.
Шаг 3: Разделите деталь на геометрические формы, которые можно легко измерить и объем которых можно вычислить. Например, разделите деталь на прямоугольники и треугольники.
Шаг 4: Вычислите объем каждой геометрической формы, используя соответствующую формулу. Например, для прямоугольника объем вычисляется как длина (l) умноженная на ширину (w) умноженную на высоту (h).
Шаг 5: Сложите все полученные объемы, чтобы получить общий объем детали в призме прямой.
Пример:
Допустим, вы измерили высоту призмы (h) равной 10 см, ширину (w) равной 5 см и глубину (d) равной 8 см. Ваша деталь имеет форму прямоугольника с размерами 4 см, 2 см и 3 см. Вычисляем объем каждой части:
Объем прямоугольника: 4 см * 2 см * 3 см = 24 см³
Общий объем детали в призме прямой:
Объем призмы: 10 см * 5 см * 8 см = 400 см³
Общий объем: 400 см³ + 24 см³ = 424 см³
Таким образом, объем детали в призме прямой равен 424 см³.