Вычисление объема многогранника является одной из фундаментальных задач геометрии. Если у вас есть многогранник с известным основанием и боковым ребром, то вы можете легко определить его объем. Для этого вам понадобятся знания о геометрических фигурах и немного математики.
Основанием многогранника может быть любая плоская фигура, например, квадрат, прямоугольник, треугольник или другая многогранная фигура. Боковыми ребрами многогранника называются ребра, которые соединяют вершины основания с соответствующими вершинами. Известные параметры многогранника позволяют вычислить его объем, используя определенные формулы и алгоритмы.
Для разных типов многогранников существуют различные способы вычисления. Например, для правильного многогранника со сторонами равными длиной, такого как куб или тетраэдр, объем можно найти с помощью формулы, которая зависит от длины стороны. Для более сложных многогранников с неравными сторонами и углами могут использоваться более сложные алгоритмы и формулы. В любом случае, может потребоваться использование тригононметрии или других математических методов для точного вычисления объема многогранника.
Как вычислить объем многогранника
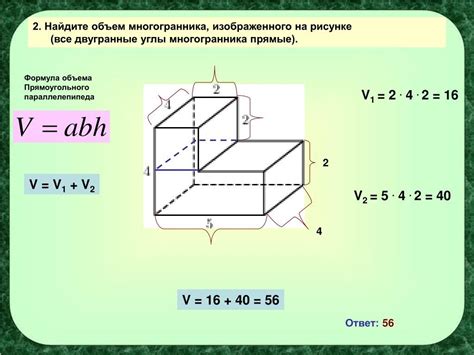
Вычисление объема многогранника зависит от его формы и свойств. Существует несколько способов вычисления объема различных многогранников, но в общем случае формула для вычисления объема выглядит следующим образом:
Объем = площадь основания × высота
Для правильных многогранников с известным основанием и высотой, формула может быть модифицирована соответствующим образом. Если основание правильного многогранника является прямоугольником, квадратом или правильным многоугольником, то площадь основания можно вычислить с помощью соответствующей формулы для данной фигуры.
Например, для правильного параллелепипеда объем вычисляется по формуле:
Объем = длина × ширина × высота
Для правильной пирамиды с известным основанием и высотой:
Объем = (площадь основания × высота) / 3
Приведенные формулы применимы для расчета объема многогранников различных форм и свойств, и могут быть использованы для решения задач из разных областей, включая геометрию, физику и инженерию.
Вычисление объема многогранника с известным основанием и боковым ребром
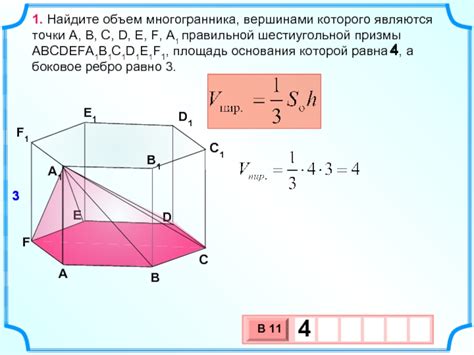
Если у вас есть многогранник с известным основанием и боковым ребром, то вы можете легко вычислить его объем. Для этого следует применить соответствующую формулу, которая зависит от типа многогранника.
Например, если ваш многогранник – прямоугольная призма, то для вычисления его объема следует умножить площадь основания на высоту. Формула для этого случая будет выглядеть следующим образом:
| Многогранник | Формула для вычисления объема |
|---|---|
| Прямоугольная призма | Объем = Площадь основания × Высота |
| Треугольная пирамида | Объем = (Площадь основания × Высота) ÷ 3 |
| Цилиндр | Объем = Площадь основания × Высота |
Для других типов многогранников также существуют соответствующие формулы для вычисления объема. Важно помнить, что площадь основания должна быть измерена в квадратных единицах, а высота – в линейных единицах.
Зная формулу для вычисления объема многогранника с известным основанием и боковым ребром, вы можете легко определить его объем и использовать эту информацию для решения различных геометрических задач или при проведении измерений в повседневной жизни.
Необходимые формулы для вычисления объема многогранника
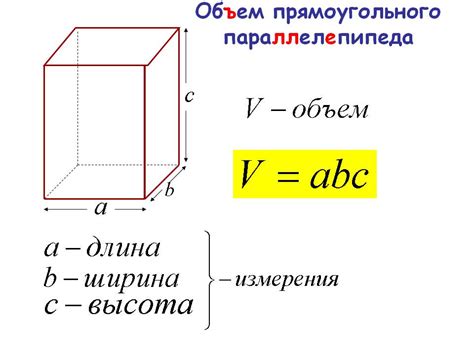
Для того чтобы вычислить объем многогранника, у которого известно основание и боковое ребро, необходимо использовать следующие формулы:
1. Площадь основания (Sосн):
Для многогранников с плоскими основаниями, площадь основания вычисляется с использованием соответствующей формулы для данной фигуры. Например, для прямоугольной призмы площадь основания равна произведению длины и ширины основания.
2. Периметр основания (Pосн):
Для многогранников с плоскими основаниями, периметр основания вычисляется как сумма длин всех сторон основания.
3. Высота многогранника (h):
Высота многогранника - это расстояние между плоскостью основания и плоскостью, параллельной основанию и проходящей через боковое ребро. Она может быть известна или вычислена с использованием других данных о многограннике.
4. Объем многогранника (V):
Для вычисления объема многогранника с известными основанием и боковым ребром используется следующая формула:
V = Sосн * h
где Sосн - площадь основания, h - высота многогранника.
Пример вычисления объема многогранника с использованием формулы
Для расчета объема данного многогранника можно воспользоваться формулой:
V = S * h
где V - объем многогранника, S - площадь основания, h - высота многогранника.
В нашем примере площадь основания правильного пятиугольника можно вычислить с помощью формулы:
S = (5 * a^2) / (4 * tan(π/5))
где a - длина стороны пятиугольника.
Высоту многогранника можно найти, зная боковое ребро и угол между основанием и боковым ребром (в нашем случае, угол равен 90 градусам).
Подставив известные значения в формулы, можем вычислить объем многогранника:
V = ((5 * a^2) / (4 * tan(π/5))) * 5
Таким образом, зная длину стороны пятиугольника, мы можем вычислить объем данной пятиугольной призмы. Удачных расчетов!