Обратная пропорциональность является одним из важных понятий в математике, которое помогает нам понять взаимосвязь между двумя переменными. В обратно пропорциональной зависимости, когда одна переменная увеличивается, другая уменьшается, и наоборот.
Определить область обратной пропорциональности можно при помощи графика или таблицы значений. Если при увеличении одной переменной другая уменьшается, то это указывает на обратную пропорциональность. Например, если мы рассматриваем зависимость между скоростью и временем, то с увеличением скорости время, потребное на преодоление расстояния, будет уменьшаться.
Как понять область обратной пропорциональности
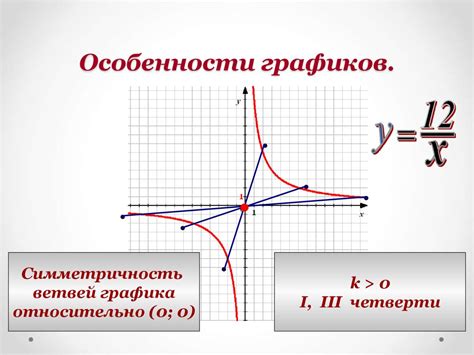
Если график имеет форму гиперболы, тогда говорят, что имеет место обратная пропорциональность. Гипербола представляет собой кривую, которая бесконечно удаляется от двух фиксированных точек, называемых фокусами. При этом, чем ближе точка к одному из фокусов, тем дальше она находится от другого.
Примером обратной пропорциональности может служить зависимость между временем выполнения задания и числом работников, занятых его выполнением. Чем больше работников, тем быстрее будет выполнено задание, и наоборот. Если мы построим график этой зависимости, то увидим, что он имеет форму гиперболы.
Важно отметить, что обратная пропорциональность может быть точной или приближенной. В точной обратной пропорциональности величины строго обратно пропорциональны друг другу, то есть их произведение всегда равно константе. В приближенной обратной пропорциональности соблюдается обратная зависимость, но произведение величин может незначительно отличаться от константы.
Таким образом, чтобы понять, что имеет место обратная пропорциональность, нужно проанализировать график зависимости между переменными. Если он имеет форму гиперболы, то можем говорить о наличии обратной пропорциональности.
Что такое обратная пропорциональность
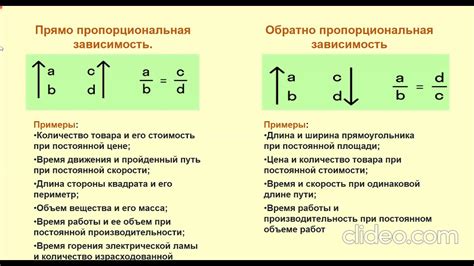
Обратная пропорциональность представляет собой математическую связь между двумя переменными, при которой увеличение одной переменной приводит к уменьшению другой переменной и наоборот. В обратной пропорции, если значения одной переменной уменьшаются, то значения другой переменной увеличиваются и наоборот.
Известно, что обратная пропорциональность может быть представлена в виде уравнения: у = k/x, где k - постоянное значение, а x и у - переменные.
Обратная пропорциональность широко используется во многих областях, таких как физика, экономика, техника и др. Например, если скорость движения тела увеличивается, то время, затраченное на преодоление определенного расстояния, уменьшается в обратной пропорции. Также, в экономической сфере, с увеличением объема производства, себестоимость единицы товара будет уменьшаться в обратной пропорции.
Определение области обратной пропорциональности позволяет строить математические модели и прогнозировать изменения величин в зависимости от их взаимосвязи. Это полезный инструмент для решения различных задач и оптимизации процессов.
Каким образом определить обратную пропорциональность

Во-первых, необходимо иметь две величины, которые можно сравнивать между собой. Обратная пропорциональность может быть выражена в виде соотношения y = k/x, где y и x – величины, а k – постоянное значение, называемое постоянной обратной пропорциональности.
В-третьих, чтобы точно определить обратную пропорциональность, нужно проверить, что при увеличении или уменьшении одной величины на определенное значение, другая величина изменяется на обратное значение с сохранением постоянной обратной пропорциональности. Если этот закономерный процесс повторяется несколько раз, можно с уверенностью утверждать, что между двумя величинами действительно существует обратная пропорциональность.
Таким образом, для определения обратной пропорциональности необходимо проанализировать изменение величин и сравнить их между собой с учетом выражения y = k/x. При наличии обратной пропорциональности величины изменяются пропорционально, иначе - это не обратная пропорция.
Как построить график для обратно пропорциональных значений

Для построения графика обратно пропорциональных значений необходимо выполнить следующие шаги:
- Составить таблицу значений с парами переменных, отображающих обратную пропорциональность.
- Найти обратные значения для каждой переменной и записать их в таблицу.
- Нанести значения переменных на координатную плоскость, где ось X отображает одну переменную, а ось Y - другую переменную.
- Соединить точки на графике, чтобы получить гладкую кривую линию. Чем больше точек, тем более точную кривую линию можно получить.
График для обратно пропорциональных значений обычно имеет форму гиперболы. Это кривая линия, состоящая из двух симметричных ветвей, расположенных вокруг фокуса. Когда одна переменная увеличивается, другая переменная уменьшается и наоборот.
Построение графика обратно пропорциональных значений позволяет наглядно визуализировать связь между двумя переменными и легче анализировать их зависимость. Такой график может быть полезным инструментом при решении различных задач, например, при определении оптимальной точки работы или установления закономерностей в данных.
Примеры задач с обратной пропорциональностью

- Задача 1: Если 5 рабочих могут выполнить работу за 12 дней, то за сколько дней эту работу сможет выполнить 10 рабочих?
- Задача 2: Если при увеличении цены на 20% количество продаж уменьшилось на 15%, то на сколько процентов необходимо снизить цену, чтобы количество продаж увеличилось на 10%?
- Задача 3: При увеличении скорости автомобиля в 2 раза, расстояние, которое он проходит, уменьшается в 3 раза. Найдите связь между скоростью и временем, необходимым для преодоления расстояния.
В данной задаче рабочие и время выполнения работы находятся в обратной пропорции. Чем больше рабочих, тем меньше времени требуется на выполнение работы. Можем построить пропорцию:
5 рабочих – 12 дней
10 рабочих – х дней (искомая величина)
По правилу обратной пропорциональности можно написать: 5 * 12 = 10 * х
Таким образом, x = (5 * 12) / 10 = 60 / 10 = 6. Ответ: 10 рабочих смогут выполнить работу за 6 дней.
В данной задаче цена и количество продаж также находятся в обратной пропорции. Можем построить пропорцию:
20% увеличение цены – 15% уменьшение продаж
х% снижение цены – 10% увеличение продаж
Можем записать: 20 * 15 = х * 10
Отсюда х = (20 * 15) / 10 = 300 / 10 = 30. Ответ: необходимо снизить цену на 30%.
В данной задаче скорость и время также находятся в обратной пропорции. Пусть v – исходная скорость, t – исходное время и d – исходное расстояние. Можем записать: v * t = d.
Если скорость увеличится в 2 раза, то новая скорость будет 2v, а время, необходимое для преодоления расстояния, будет t/3. Таким образом, новая связь между скоростью и временем будет: 2v * (t / 3) = d.
Можем упростить выражение, разделив оба выражения на t: 2v / 3 = v * t / d.
Отсюда v * t = (2v / 3) * d, или t = (2 / 3) * d / v. Ответ: время, необходимое для преодоления расстояния, равно (2 / 3) * d / v.
Приведенные примеры задач показывают, что обратная пропорциональность имеет широкое применение в различных областях: экономике, физике, геометрии и т.д. В решении таких задач важно понять, что если одна величина увеличивается, то другая уменьшается, и наоборот. Такие задачи могут показать, какой эффект будет при изменении одной величины на другую.
Как решать задачи с обратной пропорциональностью
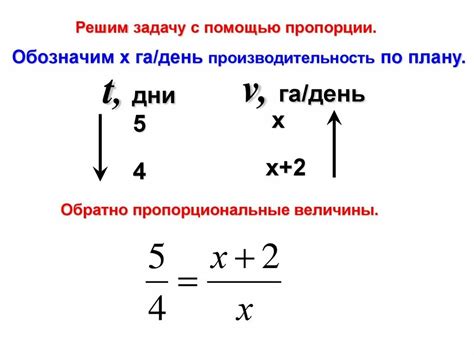
Решение задач с обратной пропорциональностью может показаться сложным, но с правильным подходом можно получить корректный ответ. Эти задачи обычно требуют определения взаимосвязи между двумя величинами, когда одна из них изменяется обратно пропорционально другой.
Вот несколько шагов, которые помогут вам решать задачи с обратной пропорциональностью:
- Определите, какие две величины в задаче являются обратно пропорциональными. Обычно, если при увеличении одной величины другая уменьшается, то между ними существует обратная пропорциональность.
- Запишите соответствующую формулу обратной пропорциональности, выразив одну величину через другую. Обычно формула имеет вид xy = k, где x и y - две величины, а k - постоянная величина.
- Используйте известные значения для одной из величин и постоянной k, чтобы выразить неизвестное значение другой величины. Обратите внимание, что при увеличении одной величины другая должна уменьшаться, и наоборот.
- Вычислите неизвестное значение и проверьте его адекватность в контексте задачи. Если значения выглядят логичными, то ваш ответ верен.
Помните, что решение задач с обратной пропорциональностью требует тщательного анализа и понимания взаимосвязей между величинами. Практика поможет вам развить навык решения таких задач, и со временем вы будете справляться с ними легче.