Область определения функции – это множество всех значений аргумента, для которых функция имеет определение. Понимание и определение области определения функции является важным этапом при обработке и анализе функций. Знание области определения позволяет понять, когда функция является определенной и когда она не имеет значения. Этот аспект имеет огромное значение не только в математике, но и в физике, экономике и компьютерных науках.
Существуют различные методы для определения области определения функции. Один из самых простых и распространенных методов – это анализ аргументов функции на предмет деления на ноль. Если входной аргумент является нулем или на него делится, то функция будет неопределена в этой точке. Кроме того, стоит обратить внимание на радикалы, логарифмические и тригонометрические функции, которые также могут иметь ограничения на свою область определения.
Рассмотрим пример для наглядности. Пусть дана функция f(x) = 1 / (x - 2). Чтобы определить ее область определения, нужно исследовать, при каких значениях аргумента функция будет определена. В данном случае функция не определена при x = 2, так как это значение делит на ноль, поэтому область определения функции будет состоять из всех действительных чисел, кроме x = 2.
Что такое область определения функции

Область определения функции может быть ограничена или неограничена. Ограниченная область определения означает, что существуют некоторые ограничения на значения аргументов. Например, функция может быть определена только для положительных чисел или только для чисел из определенного интервала.
Чтобы определить область определения функции, необходимо учесть все ограничения, налагаемые на функцию. Это может быть множество значений, для которых функция имеет определение, или интервалы, в которых функция не имеет разрывов и принимает определенные значения.
Область определения функции важна для понимания ее поведения и возможности вычисления значений. Если значение аргумента не входит в область определения функции, то она не может быть вычислена для этого значения.
Например, функция f(x) = 1/x имеет область определения всех вещественных чисел, кроме x = 0, так как деление на ноль не определено.
Определение области определения функции является важным шагом в анализе и работы с функциями. Это помогает избежать ошибок и понять, какие значения аргументов допустимы для данной функции.
Понятие области определения и ее значение в математике

Область определения может быть задана разными способами, в зависимости от типа функции. Например, для функций с алгебраическими выражениями область определения может быть задана с помощью условий, которые ограничивают значения переменных. Для тригонометрических функций область определения может быть ограничена диапазоном значений аргумента, при которых функция существует.
| Тип функции | Область определения |
|---|---|
| Алгебраическая функция | Все значения переменных, при которых функция имеет смысл |
| Тригонометрическая функция | Значения аргумента в определенном диапазоне (например, от -π до π) |
| Экспоненциальная функция | Все действительные значения аргумента |
| Логарифмическая функция | Положительные значения аргумента |
Знание области определения функции позволяет определить, при каких значениях аргумента функция имеет смысл и может быть вычислена. Это очень важно, так как при попытке вычислить функцию вне ее области определения результат будет неопределенным или некорректным. Например, попытка взять логарифм от отрицательного числа приведет к неопределенности.
Таким образом, понятие области определения является важной составляющей математического анализа и позволяет определить, когда функция имеет смысл и может быть корректно вычислена.
Методы определения области определения функции

1. Аналитический метод:
Аналитический метод заключается в анализе алгебраической записи функции. Для определенных классов функций, таких как рациональные, иррациональные или логарифмические функции, можно определить область определения, применяя соответствующие математические правила и свойства.
2. Графический метод:
Графический метод заключается в построении графика функции. Если график функции не имеет разрывов, то область определения будет множеством всех значений аргументов, ограниченным границами графика.
3. Символьный метод:
Символьный метод основан на анализе символов, встречающихся в записи функции. Например, функция с корнем не может принимать отрицательные значения под корнем, поэтому область определения будет множеством всех действительных чисел, кроме отрицательных.
4. Числовой метод:
Числовой метод заключается в подстановке различных значений аргументов в функцию и анализе результата. Если функция имеет разрывы или неопределенные значения при определенных значениях аргументов, то эти значения будут исключены из области определения.
5. Комбинированный метод:
Комбинированный метод заключается в использовании нескольких методов одновременно для определения области определения функции. Этот метод может быть полезен при сложных функциях, когда один метод может недостаточно точно определить область определения.
Важно помнить, что каждая функция имеет свои особенности, и методы определения области определения могут отличаться в зависимости от типа функции. Поэтому при исследовании функций рекомендуется применять разные методы и проверять результаты друг другом для достижения более точных и надежных результатов.
Метод графика для определения области определения
Для определения области определения функции с помощью графика, необходимо построить график функции на координатной плоскости и анализировать его свойства. Ниже приведены шаги, которые позволят вам использовать метод графика для определения области определения функции:
- Постройте график функции на координатной плоскости. Для этого можно использовать различные методы, включая построение графика вручную или с использованием программных инструментов, таких как графические калькуляторы или математические программы.
- Анализируйте график функции, обращая внимание на пересечения графика с осями координат. Если график функции пересекает ось абсцисс в определенной точке, это означает, что функция определена в этой точке. Однако, если график функции не пересекает ось абсцисс в определенной точке, то функция не определена в этой точке.
- Продолжайте анализировать график функции, обращая внимание на его поведение вне основной части графика. Если график функции имеет асимптоты или специальные точки, например разрывы или точки разрывов, это может указывать на ограничения в определении функции в этих областях.
Используя метод графика для определения области определения функции, вы можете получить представление о значениях, которые функция принимает в различных точках оси координат. Это поможет вам определить область определения функции и понять, в каких точках функция неопределена.
Пример:
| x | f(x) |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
В данном примере график функции представляет собой параболу, открывшуюся вверх. Из графика видно, что функция определена для всех действительных значений x. Область определения функции равна (-∞, +∞).
Метод анализа формул для определения области определения
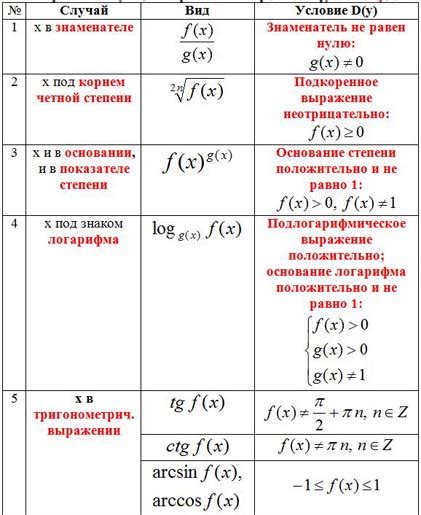
Для начала необходимо разобраться в формуле функции и выделить все ограничения и оговорки, которые заданы в исходной задаче. Например, если функция содержит выражения под знаком корня или деления на ноль, то эти значения будут являться точками, в которых функция не определена.
Анализ формулы функции может быть сложен, особенно если формула состоит из нескольких компонентов или содержит сложные выражения. В таких случаях помогает знание основных математических правил и свойств функций, а также умение упрощать и преобразовывать выражения.
Одним из наиболее часто встречающихся ограничений является деление на ноль. Если в формуле функции присутствует деление на переменную или выражение, то необходимо исключить из множества значений аргумента те значения, при которых происходит деление на ноль. Например, если функция имеет вид f(x) = 1/(x-1), то аргумент не может принимать значение 1, так как в этом случае происходит деление на ноль.
Также стоит обратить внимание на наличие корней в формуле. Если в формуле функции имеются выражения под корнем, то аргумент не может принимать значения, при которых подкоренное выражение отрицательное. Например, если функция имеет вид g(x) = √(x-3), то аргумент не может быть меньше 3, так как в этом случае подкоренное выражение будет отрицательным.
Помимо деления на ноль и наличия корней, также могут быть другие ограничения в формуле функции, такие как логарифм с отрицательным аргументом или выражение в знаменателе дроби, равное нулю.
Важно помнить, что некоторые функции могут быть определены на всей числовой прямой, то есть иметь бесконечную область определения. Однако даже в таких случаях необходимо провести анализ формулы и исключить возможные ограничения.
Таким образом, метод анализа формулы для определения области определения функции позволяет выявить все значения аргумента, при которых функция не определена или имеет некоторые ограничения. Этот метод является одним из ключевых при решении задач по определению области определения функций.
Примеры определения области определения функции

Приведем несколько примеров, как определить область определения функции:
1. Простейшие функции
Для простейших функций, таких как f(x) = k или f(x) = x, область определения будет состоять из всех реальных чисел. Например, если f(x) = 2x + 3, то область определения будет (-∞, +∞).
2. Рациональные функции
Для рациональных функций, область определения будет составлять все значения x, за исключением тех, которые делают знаменатель равным нулю. Например, если f(x) = 1/x, то область определения будет (−∞, 0) ∪ (0, +∞).
3. Квадратные корни
Для функций с квадратными корнями, область определения будет состоять из тех значений x, для которых выражение под корнем неотрицательно. Например, если f(x) = √(4 - x^2), то область определения будет [-2, 2], так как 4 - x^2 должно быть больше или равно нулю.
4. Функции с логарифмами
Для функций с логарифмами, область определения будет составлять все значения x, для которых аргумент логарифма положительный. Например, если f(x) = log(x), то область определения будет (0, +∞), так как логарифм определен только для положительных чисел.
Это лишь несколько примеров определения области определения функции. В каждом случае необходимо брать во внимание особенности самой функции и ограничения, которые она накладывает на свои переменные.