Определение области определения функции - это важный шаг в математике, который позволяет понять, на каких значениях аргумента функция определена. Знание области определения помогает избежать ошибок при работе с функциями и позволяет правильно интерпретировать их результаты.
Область определения функции может быть ограничена различными условиями, такими как корень из отрицательного числа, деление на ноль или наличие логарифма с отрицательным аргументом. Чтобы определить область определения функции, требуется провести анализ каждого из этих условий.
Для начала, необходимо исключить значения аргументов, при которых функция не имеет смысла или ведет себя некорректно. Например, если функция содержит корень из отрицательного числа, то область определения будет ограничена значениями аргумента, для которых аргумент не является отрицательным числом.
После исключения этих особых значений, можно проверять другие условия, такие как деление на ноль или логарифмы с отрицательными аргументами. Также может потребоваться учесть дополнительные условия, указанные в задаче или контексте.
Определение понятия "Область определения"
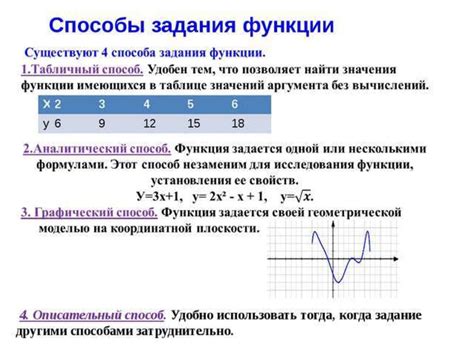
Область определения функции можно представить в виде таблицы, где в левом столбце указываются значения аргументов, а в правом столбце - соответствующие им значения функции.
Например, для функции f(x) = √x, область определения будет состоять из всех неотрицательных значений аргумента x, так как нельзя извлечь квадратный корень из отрицательного числа.
| Аргумент (x) | Значение функции (f(x)) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
В данном примере, область определения функции f(x) = √x будет состоять из всех неотрицательных чисел, то есть [0, +∞).
Важно учитывать область определения функции при решении задач, а также при построении ее графика или вычислении значений функции.
Почему важно знать область определения функции

- Избегание ошибок: Знание области определения позволяет избежать ошибок при вычислении значения функции для недопустимого аргумента. Это особенно важно при программировании, где некорректные значения аргументов могут привести к сбоям системы или неправильным результатам расчетов.
- Определение условий применимости: Зная область определения функции, можно определить условия, при которых функция может быть использована. Это позволяет рационально использовать функцию в различных контекстах и избегать некорректного использования.
- Расширение области функции: Знание области определения позволяет легче определить, как можно расширить функцию и сделать ее более универсальной. Понимая предельные значения аргументов функции, можно более эффективно определить ее границы и внести изменения, чтобы функция сохраняла свои свойства и корректность при расширении области определения.
В целом, знание области определения функции способствует более глубокому и точному пониманию функции, ее свойств и поведения. Это позволяет более эффективно работать с функциями и использовать их в различных математических и информационных задачах.
Первый способ определить область определения функции

Чтобы определить область определения функции, необходимо рассмотреть все переменные в выражении и исследовать, существуют ли ограничения на их значения.
Например, рассмотрим функцию:
f(x) = √x
В этом примере переменная x является аргументом функции. Область определения этой функции включает все неотрицательные значения x, так как квадратный корень из отрицательного числа не существует в обычной арифметике.
Таким образом, область определения функции f(x) = √x равна:
D = x >= 0
Этот способ определения области определения функции является одним из наиболее распространенных и простых в использовании. Однако, в некоторых случаях он может быть неэффективным или неприменимым.
Второй способ определить область определения функции

1. Знаменатели дробей: функция может не быть определена, если значение в знаменателе равно нулю. Например, функция f(x) = 1/(x-3) не определена при x=3.
2. Извлечение корня: под корнем не могут быть отрицательные значения или нули в знаменателе. Например, функция g(x) = sqrt(x+4) будет определена только при x >= -4.
3. Логарифмические функции: логарифмы определены только для положительных значений аргумента. Например, функция h(x) = log(x) будет определена только при x > 0.
4. Выражения с искусственным ограничением: в некоторых случаях область определения может быть ограничена условием задачи или дополнительными требованиями. Например, функция k(x) = 1/x будет определена для всех значений x, кроме x=0.
5. Сложные выражения: если функция представлена в виде сложного выражения, то необходимо проанализировать каждую его составляющую и определить область определения каждой из них. Затем области определения можно объединить.
| Функция | Область определения |
|---|---|
| f(x) = 1/(x-3) | x ≠ 3 |
| g(x) = sqrt(x+4) | x ≥ -4 |
| h(x) = log(x) | x > 0 |
| k(x) = 1/x | x ≠ 0 |
Используя алгоритмы анализа алгебраических выражений и учитывая особенности конкретной функции, можно определить ее область определения.
Третий способ определить область определения функции

Чтобы найти эти значения, нужно решить уравнение, полученное приравнивании знаменателя или аргумента под корнем или в знаменателе логарифма или экспоненты к нулю и исключить полученные значения из области определения функции.
Пример:
- Рассмотрим функцию f(x) = 1 / (x - 2). Заметим, что знаменатель не может быть равен нулю. Поэтому x - 2 ≠ 0.
- Решим это уравнение: x ≠ 2.
- Таким образом, область определения функции f(x) = 1 / (x - 2) - это все значения x, кроме 2.
Итак, третий способ определить область определения функции - это найти значения аргумента, при которых функция принимает бесконечность или неопределенное значение. Найденные значения необходимо исключить из области определения функции.