Определение области определения функции с модулем является важным шагом в анализе функций, особенно при работе с функциями, содержащими модуль. Область определения функции - это набор всех входных значений, для которых функция определена и возвращает результат. Однако, определить область определения функции с модулем может быть сложнее, чем с обычными функциями.
Модуль в функции может быть задан с помощью функции модуля ABS, которая возвращает абсолютное значение числа, то есть его модуль. В таких случаях, функция может быть определена для всех входных значений, кроме нуля. Например, функция f(x) = |x| определена для любого входного значения, кроме x = 0.
Чтобы определить область определения функции с модулем, можно использовать следующие правила:
- Если модуль находится в знаменателе дроби, то функция определена для всех входных значений, за исключением нуля. Например, функция f(x) = 1/|x| определена для любого входного значения, кроме x = 0.
- Если модуль находится внутри арифметического выражения с переменными, то функция определена для всех входных значений. Например, функция f(x) = |x + 2| определена для любого входного значения x.
- Если переменная является аргументом внутри модуля, то функция определена для всех входных значений. Например, функция f(x) = |sin(x)| определена для любого входного значения x.
Знание области определения функции с модулем позволяет изучать и анализировать функцию, а также проводить различные операции с ней, такие как поиск экстремумов и построение графика.
Определение области определения функции с модулем

Для определения области определения функции с модулем необходимо учитывать особенности данного математического оператора. Модуль числа возвращает его абсолютное значение, то есть модуль отрицательного числа равен положительному числу с тем же значением.
Основное правило определения области определения функции с модулем заключается в том, что выражение под модулем должно быть неотрицательным. Если в исходной функции символ под модулем может быть отрицательным, то нужно использовать условие для установления границ области определения.
Для примера, рассмотрим функцию с модулем: f(x) = |x - 3|.
Значение выражения (x - 3) может быть отрицательным, поэтому нужно учитывать все возможные случаи:
- Если x - 3 ≥ 0, то область определения функции f(x) содержит все значения x, которые больше или равны 3.
- Если x - 3 < 0, то область определения функции f(x) содержит все значения x, которые меньше 3.
Таким образом, область определения данной функции с модулем - все действительные числа.
Правила определения области определения функции с модулем можно обобщить следующим образом:
- Определить выражение под модулем и выяснить, может ли оно быть отрицательным.
- Если выражение под модулем может быть отрицательным, необходимо проверить значения, при которых оно меняет знак.
- Установить границы области определения на основе результатов предыдущих шагов.
Используя эти правила, можно определить область определения функций с модулем и гарантировать корректное использование этого математического оператора.
Понятие и примеры функций с модулем
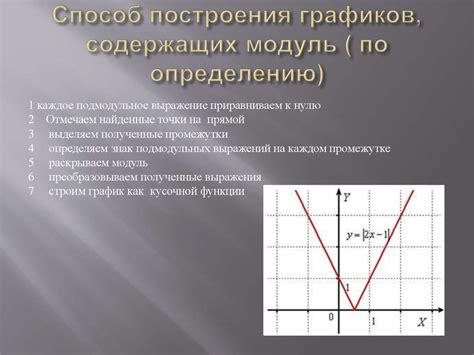
Примером функции с модулем может служить функция модуля: f(x) = |x|. В этом случае, независимо от значения аргумента x, функция вернет его абсолютное значение. Например, для x = -5, значение функции будет 5. Если x = 2, значением функции будет 2.
Другой пример функции с модулем может быть функция с условием: f(x) = |x - 2|. В этом случае, аргумент x отличный от 2 будет возвращать абсолютное значение разности x и 2. Например, при x = 3, значение функции будет 1 (|3 - 2| = 1). А при x = -1, значение функции будет 3 (|-1 - 2| = 3).
Также примерами функций с модулем могут служить функции, содержащие в себе другие математические операции, такие как сложение, вычитание, умножение или деление, в зависимости от конкретной задачи или условия.
Как найти область определения функции с модулем

Определение области определения функции с модулем может быть нетривиальной задачей. Однако, существуют основные правила, которые помогут в определении этой области.
Перед тем как рассмотреть правила определения области определения функции с модулем, необходимо понимать, что модуль числа – это значение числа, без учета его знака. То есть, модуль числа всегда положителен или равен нулю.
1. Для функций с модулем, содержащим переменную в знаменателе, необходимо исключить значение переменной, при котором знаменатель обращается в ноль. Так как знаменатель не может быть равным нулю, эти значения не входят в область определения функции.
| Пример | Область определения |
|---|---|
| f(x) = 1 / |x - 3| | x ≠ 3 |
| g(x) = 1 / |2x + 1| | x ≠ -1/2 |
2. Если функция с модулем является аргументом другой функции, то область определения будет зависеть от области определения этой другой функции.
| Пример | Область определения |
|---|---|
| f(x) = sin(|x + 1|) | x ∈ (-∞, ∞) |
| g(x) = log(|2x - 3|) | x > 3/2 |
3. Если функция с модулем находится внутри корня, то необходимо исключить значения, при которых модуль числа становится отрицательным или комплексным. Такие значения не входят в область определения функции.
| Пример | Область определения |
|---|---|
| f(x) = √(|x - 5|) | x ≥ 5 |
| g(x) = √(|2x + 1|) | x ≥ -1/2 |
Используя эти основные правила, можно определить область определения функций с модулем. При решении задач, необходимо также учитывать другие условия, которые могут быть связаны с конкретной функцией.
Основные правила определения области определения функции с модулем

1. Начальное определение ОО функции. Если у функции нет модуля, то её ОО определяется выражением под корнем, если такое существует, иначе ОО состоит из всех допустимых значений независимой переменной.
2. Определение ОО функции с модулем в исключительных случаях. В некоторых случаях, при определении ОО функции с модулем, возможно появление исключительных значений, при которых функция не определена. Например, если внутри модуля находится выражение, которое будет равно нулю в знаменателе дроби. В таком случае, ОО функции с модулем может быть определена как множество значений независимой переменной, исключая исключительные значения.
3. Определение ОО функции с модулем при различных случаях. В зависимости от различных случаев, при определении ОО функции с модулем, могут возникать следующие ситуации:
- Модуль внутри линейной функции: ОО состоит из всех значений независимой переменной, при которых линейная функция, внутри модуля, определена.
- Модуль внутри квадратичной функции: ОО состоит из всех значений независимой переменной, при которых квадратичная функция, внутри модуля, определена, исключая исключительные значения.
- Модуль внутри рациональной функции: ОО состоит из всех значений независимой переменной, при которых рациональная функция, внутри модуля, определена, исключая исключительные значения.
- Модуль внутри иррациональной функции: ОО состоит из всех значений независимой переменной, при которых иррациональная функция, внутри модуля, определена, исключая исключительные значения.
При определении ОО функции с модулем необходимо учитывать все данные правила и находить значения независимой переменной, при которых функция будет определена и иметь смысл.