Когда мы говорим о функциях с производными, важно понимать, что не все значения аргументов могут быть допустимыми для таких функций. Область определения функции – это множество всех возможных значений аргумента, при которых функция определена и имеет смысл. Чтобы определить область определения функции с производной, необходимо учесть ограничения, которые накладывает производная на ее значения.
Один из способов определить область определения функции с производной – это исследование точек разрыва функции. Точки разрыва могут быть классифицированы на разрывы первого рода, разрывы второго рода и устранимые разрывы. Для каждого типа разрыва можно определить, включается ли он в область определения функции.
Еще один метод определения области определения – это анализ границ функции. Границы могут быть обусловлены, например, корнями уравнения, знаменателем функции или ограничениями на значение аргумента. Исследование границ помогает определить, при каких значениях аргумента функция является определенной и имеет производную.
Что такое область определения функций с производной?

Для того чтобы определить область определения функции с производной, необходимо обратить внимание на несколько факторов:
- Функция должна быть определена на всем своем области определения.
- Функция должна быть непрерывна на всем своем области определения.
- Функция должна иметь конечную производную на всем своем области определения.
- Функция должна быть дифференцируема на всем своем области определения, кроме, возможно, некоторого конечного числа точек, в которых она может иметь разрывы.
В область определения функции с производной могут входить как вещественные числа, так и комплексные числа, в зависимости от свойств функции и ее аргумента. Область определения может быть ограничена или неограничена.
Определение области определения

Для определения области определения функции с производной, необходимо учитывать два фактора:
- Значения, для которых функция является определенной:
- Если функция содержит радикал, необходимо проверить, какие значения аргумента делают подкоренное выражение отличным от нуля.
- Если функция содержит дробную часть, необходимо проверить, какие значения аргумента делают знаменатель отличным от нуля.
- Значения, для которых функция не имеет производной:
- Если функция содержит модуль, необходимо учесть его границы и определить интервалы, на которых функция может не быть дифференцируемой.
- Если функция содержит разрыв, необходимо учесть точки разрыва и определить интервалы, на которых функция может не быть дифференцируемой.
Получив все значения, для которых функция является определенной и значения, для которых функция не имеет производной, можно определить область определения функции. Она представляет собой объединение интервалов, на которых функция является определенной и имеет производную.
Как определить область определения функции?

1. В начале анализа функции следует исключить значения аргументов, при которых функция будет неопределена. Например, нельзя делить на 0 или брать корень из отрицательного числа.
2. Затем следует исследовать область определения каждой подфункции, если функция состоит из нескольких подфункций.
3. Также стоит обращать внимание на то, что в некоторых случаях функции могут иметь несколько значений в области определения или наоборот, не иметь значений.
4. Когда функция задана в виде формулы, нужно проанализировать возможные ограничения на значения аргументов, которые вытекают из этой формулы. Например, если в формуле есть логарифм, то аргумент логарифма может быть только положительным числом.
Все эти шаги помогут определить область определения функции и понять, для каких значений аргументов функция имеет смысл и может быть вычислена.
Производная функции
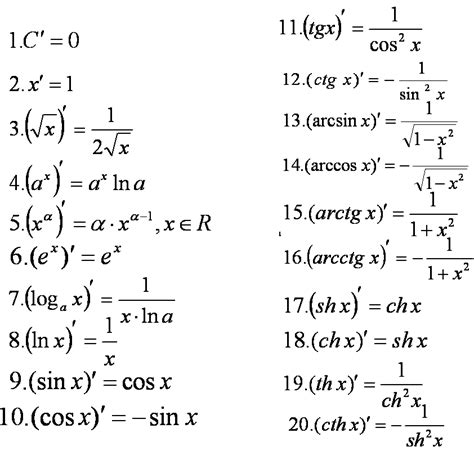
Производная функции выражается через предел приращения функции и приращения аргумента. Если функция задана аналитически, то ее производная может быть найдена с помощью определенных правил дифференцирования.
Производная функции может иметь различные значения в разных точках области определения. В зависимости от знака производной, можно определить, в каких точках функция возрастает или убывает. Точки, где производная обращается в ноль, называются критическими точками.
Производная функции также позволяет определить наличие экстремумов в функции и их тип (максимум или минимум). Для этого необходимо исследовать поведение производной в окрестности критической точки.
На практике производные функций используются во многих областях, таких как физика, экономика и информатика. Они позволяют оценить изменение величины или скорость изменения какого-либо процесса, и являются важным инструментом для исследования и оптимизации различных систем и процессов.
| Примеры производных функций | Производная |
|---|---|
| константа: f(x) = c | f'(x) = 0 |
| степенная функция: f(x) = x^n | f'(x) = n*x^(n-1) |
| экспонента: f(x) = e^x | f'(x) = e^x |
| синус: f(x) = sin(x) | f'(x) = cos(x) |
| косинус: f(x) = cos(x) | f'(x) = -sin(x) |
Что такое производная функции?

$$f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$$
Значение производной функции в конкретной точке обозначается как $$f'(x)$$ или $$\frac{df}{dx}$$. Оно показывает, насколько функция меняется при малом изменении аргумента в данной точке. Если производная положительна, то функция возрастает, если производная отрицательна, то функция убывает. При этом значение производной в точке можно рассматривать как тангенс угла наклона касательной к графику функции в данной точке.
Производная функции является важным инструментом для анализа поведения функции и решения различных математических задач. Она позволяет находить экстремумы функции, определять ее поведение в каждой точке, а также строить приближенные графики функций.
Для определения области определения функций с производной необходимо исследовать, на каких интервалах производная функции существует и не меняет знак. Это позволит определить непрерывность и монотонность функции, а также понять, где возможны условия на ее аргументы. Знание производной функции позволяет более точно анализировать их поведение и применять в различных областях, таких как физика, экономика и другие.
Определение области определения функций с производной

Для определения области определения функции с производной, необходимо учесть следующие факторы:
- Знаки корней и знаки разности значений в знаменателе. Если функция содержит знаменатель, то необходимо исключить значения аргумента, при которых знаменатель равен нулю или изменяет знак. Такие точки называются точками разрыва функции. Например, если знаменатель равен нулю при аргументе x=2, то точка x=2 не входит в область определения функции.
- Знаки выражения под корнем. Если функция содержит корень, то значения аргумента должны быть такими, чтобы выражение под корнем было неотрицательным. Например, если функция содержит выражение под корнем √(x+1), то необходимо исключить значения аргумента, при которых x+1
- Область определения других составных функций. Если функция представлена в виде составной функции, то необходимо учесть область определения внутренних функций. Например, если функция задана как f(x) = sin(x^2), то область определения функции sin(x^2) будет зависеть от области определения функции x^2. В данном случае, функция x^2 определена при любых значениях x, поэтому область определения функции sin(x^2) будет равна всей числовой прямой.
Определение области определения функции с производной позволяет более точно определить дифференцируемость и производную функции в каждой точке области определения. Результатом является набор значений аргумента, при которых функция определена и может быть дифференцирована.