Функции синуса и косинуса являются основными функциями в тригонометрии и широко применяются в математике, физике и других науках. Они описывают зависимость угла от координат точки на окружности и имеют множество свойств и приложений.
Одним из важных аспектов при работе с функциями синуса и косинуса является определение их области определения. Область определения функции задает множество значений, для которых функция имеет смысл и может быть вычислена.
Для функции синуса область определения включает все действительные числа, так как синус можно вычислить для любого угла. Однако, если синус рассматривается как периодическая функция, то ее область определения может быть ограничена определенным интервалом углов.
Функция косинуса также имеет область определения, которая включает все действительные числа. Как и в случае с синусом, для косинуса можно найти значение для любого угла. Однако, как и с синусом, для косинуса также можно рассмотреть определенные интервалы углов в контексте его периодической природы.
Как определить область определения функции синуса и косинуса

Функция синуса (обозначается как sin) определена для всех углов, независимо от их размера. Область определения sin(x) – это все действительные числа, так как углы могут быть измерены в радианах, градусах или градах. Sin(x) принимает значения от -1 до 1 и имеет период 2π.
Функция косинуса (обозначается как cos) также определена для всех углов. Область определения cos(x) также включает все действительные числа. Как и sin(x), cos(x) принимает значения от -1 до 1 и имеет период 2π.
Чтобы вычислить значения функций sin(x) и cos(x) за пределами их областей определения, необходимо использовать математические методы расширения области определения, такие как продолжение функции или тригонометрические тождества. Однако, для большинства практических целей, область определения sin(x) и cos(x) считается равной всем действительным числам.
Определение функции синуса и косинуса
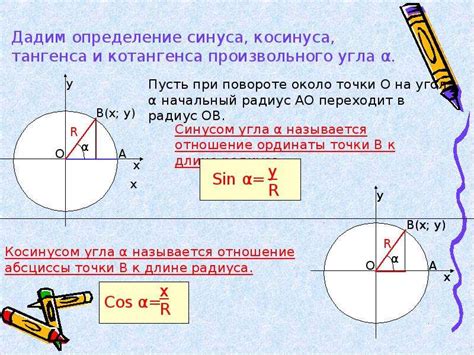
Синус и косинус определяют соответствующие значения координат точки на единичной окружности, на которой угол между начальной точкой и выбранной точкой задает значение аргумента функции.
| Угол (в радианах) | Синус | Косинус |
|---|---|---|
| 0 | 0 | 1 |
| π/6 | 1/2 | √3/2 |
| π/4 | √2/2 | √2/2 |
| π/3 | √3/2 | 1/2 |
| π/2 | 1 | 0 |
| π | 0 | -1 |
Таблица показывает значения синуса и косинуса для некоторых углов в радианах, но эти функции определены для любых углов вне зависимости от их значений. Используя тригонометрические функции синуса и косинуса, мы можем решать задачи в геометрии, физике, а также анализировать периодические явления.
Область определения функций синуса и косинуса

Функция синуса (sinx) определена для всех действительных чисел. Значения синуса лежат в диапазоне [-1, 1]. Синус достигает своего максимального значения 1 при x = π/2 + 2nπ, где n - целое число, и своего минимального значения -1 при x = 3π/2 + 2nπ.
Функция косинуса (cosx) также определена для всех действительных чисел. Значения косинуса также лежат в диапазоне [-1, 1]. Косинус достигает своего максимального значения 1 при x = 2nπ, где n - целое число, и своего минимального значения -1 при x = π + 2nπ.
Область определения функций синуса и косинуса необходимо учитывать при решении уравнений с использованием этих функций, а также при изучении их свойств и графиков.