Как определить область определения и значения функции Гайд

Функция Гайд (или гейд) приобрела свое название в честь американского математика Вильяма Гейда. Она является элементарной функцией, которая часто встречается в задачах и теории функций. Понимание области определения и значения этой функции является необходимым для успешного решения различных математических задач.

Область определения функции Гайд - это множество всех значений аргумента функции, при которых она имеет смысл и является определенной. В случае функции Гайд, область определения включает в себя все действительные числа, за исключением нуля и единицы.

Значение функции Гайд зависит от значения аргумента. Функция Гайд может принимать значения отрицательные, положительные и нулевые. Особенностью функции Гайд является то, что она не является непрерывной на всей своей области определения. В точках ноль и единица функция не определена.

Что такое функция Гайд?

Функция Гайд может быть представлена графиком, где по оси абсцисс располагаются входные значения, а по оси ординат – соответствующие выходные значения. Такой график называется графиком функции.

Областью определения функции Гайд является множество всех возможных входных значений, при которых функция определена. Значением функции является результат, полученный при подстановке конкретного входного значения.

Функция Гайд может иметь различные формы и свойства, такие как линейная, квадратичная, показательная, логарифмическая и многие другие. Она широко используется в различных областях науки, техники, экономики и других дисциплинах для моделирования и анализа различных процессов и явлений.

Изучение функций Гайд позволяет понять взаимосвязь между переменными и прогнозировать изменения выходных значений при изменении входных параметров.

Понятие функции Гайд и ее особенности

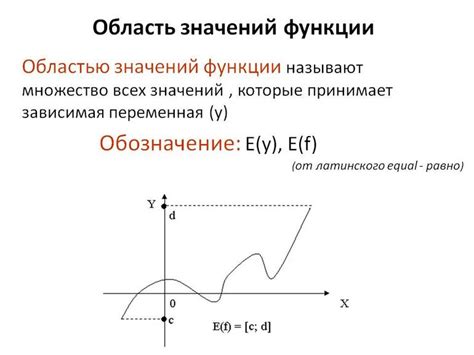
Основной отличительной особенностью функции Гайд является ее определенная область значений и область определения. Область значений представляет собой множество значений, которые может принимать функция, а область определения – множество значений, для которых функция определена.

Функция Гайд может быть задана аналитическим выражением, которое позволяет вычислять значения функции при заданных входных данных. Однако, в некоторых случаях функция Гайд может быть задана и графически, то есть с помощью графика, который отображает зависимость значения функции от ее аргумента.

Как определить область функции Гайд

Для определения области функции Гайд необходимо выполнить несколько шагов:

1. Найти все ограничения, которые могут присутствовать в функции, такие как: деление на ноль, аргументы, которые входят в комплексную область, логарифмы и корни с отрицательными значениями и т. д.
2. Определить значения, при которых эти ограничения выполняются или нарушаются.
3. Исключить все значения, при которых ограничения нарушены, и получить область, в которой функция может быть определена.

Например, если функция содержит выражение под корнем, необходимо исключить все значения, при которых оно отрицательно, так как корень из отрицательного числа не существует. Аналогично, если функция содержит деление на переменную, нужно исключить все значения переменной, при которых оно равно нулю, так как деление на ноль невозможно.

Полученная область будет представлять собой интервалы значений переменных, при которых функция определена.

Алгоритм определения области функции Гайд

Для определения области функции Гайд необходимо выполнить следующий алгоритм:

Шаг 1: Найдите все значения аргументов, для которых функция определена. Это значит, что функция не может быть вычислена при некоторых специальных значениях аргументов, например, при делении на ноль или при извлечении квадратного корня из отрицательного числа.

Шаг 2: Определите все ограничения, которые накладываются на значения аргументов. Например, функция может быть определена только для положительных значений аргументов или только для целых чисел.

Шаг 3: Найдите все значения функции, используя найденные значения аргументов. Для этого подставьте найденные значения аргументов в функцию и вычислите соответствующие значения функции.

Полученные значения функции являются всевозможными значениями, которые она может принимать в определенной области. Если значения функции ограничены, то область функции будет состоять из интервала или множества значений, в которых она может находиться.

Пример:

Рассмотрим функцию f(x) = 1/(x-2). Шаги определения области функции для этого примера:

Шаг 1: Функция не определена при x = 2, так как в этом случае происходит деление на ноль.

Шаг 2: Функция определена для любого действительного значения x, за исключением x = 2.

Шаг 3: Подставим значения аргументов в функцию:

Таким образом, область функции Гайд для функции f(x) = 1/(x-2) является множеством всех действительных чисел, кроме x = 2, с соответствующими значениями функции.

Как найти значение функции Гайд

Для определения значения функции Гайд необходимо подставить значение аргумента в математическое выражение, описывающее данную функцию, и выполнить соответствующие вычисления.

Функция Гайд представляет собой алгоритмическую последовательность действий, которую можно описать с помощью математических выражений. Обычно функция Гайд задается формулой или графиком, и ее значение зависит от значений аргументов, переданных в функцию.

Чтобы найти значение функции Гайд, следует:

1. Определить значение аргумента.
2. Подставить значение аргумента в выражение, описывающее функцию Гайд.
3. Выполнить вычисления согласно заданным математическим правилам.
4. Полученный результат является значением функции Гайд при данном значении аргумента.

Пример:

Пусть функция Гайд задана следующим выражением: f(x) = 2x + 3. Для нахождения значения функции при заданном значении аргумента, например, x = 5, необходимо подставить это значение в выражение: f(5) = 2 * 5 + 3. Выполняя вычисления, получаем: f(5) = 13.

Таким образом, значение функции Гайд при аргументе x = 5 равно 13.