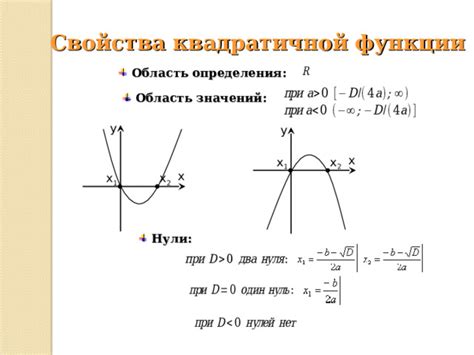
Одной из важных тем в учебной программе 9 класса по математике является изучение квадратичных функций. Квадратичная функция – это функция вида y = ax^2 + bx + c, где a, b и c - это числа, известные как коэффициенты. Область определения квадратичной функции - это набор всех допустимых значений аргумента x, при которых функция имеет смысл.
Для определения области определения квадратичной функции необходимо учесть, что значение аргумента x может быть любым действительным числом. То есть, нет никаких ограничений на значение x в квадратичной функции. Однако, стоит помнить, что для некоторых значений аргумента x, функция может принимать значения, которые на практике не имеют смысла. Например, если квадратичная функция моделирует зависимость времени от расстояния, то отрицательные значения аргумента x (расстояния) не имеют физического смысла и следует исключить из области определения.
Следовательно, область определения квадратичной функции определяется как множество всех действительных чисел, за исключением некоторых значений, которые могут привести к несоответствующим или физически невозможным значениям функции. Для эффективного определения области определения рекомендуется визуализировать квадратичную функцию с помощью графика или использовать математические методы, такие как вычисление дискриминанта или нахождение корней квадратного уравнения.
Что такое область определения квадратичной функции?
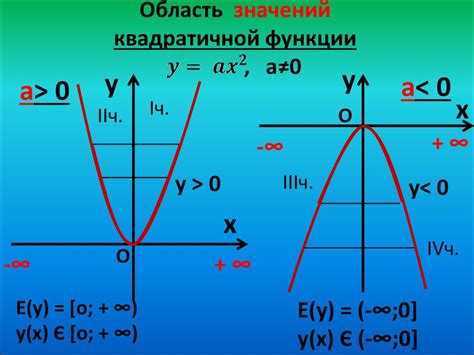
Квадратичная функция имеет общую форму f(x) = ax^2 + bx + c, где a, b и c - коэффициенты функции, и x - переменная аргумента. Квадратичная функция является параболой, и ее область определения будет зависеть от коэффициента a.
Если коэффициент a не равен нулю, то функция определена для всех действительных чисел. То есть область определения будет равна множеству всех действительных чисел.
Однако, если коэффициент a равен нулю, то квадратичная функция не будет иметь квадратичной формы и перейдет в линейную функцию. В этом случае, функция будет определена только для некоторых значений аргумента x, и область определения будет ограничена.
Чтобы определить область определения квадратичной функции, можно обратиться к графику функции или использовать аналитические методы, такие как расчет дискриминанта. Дискриминант функции поможет определить, когда квадратичная функция будет иметь решение, и тем самым определить ее область определения.
Важно знать область определения квадратичной функции, так как она позволяет определить, какие значения можно подставить в функцию для получения результатов. Это важное понятие позволяет избегать ошибок при использовании квадратичных функций и понять, как варьируются их результаты.
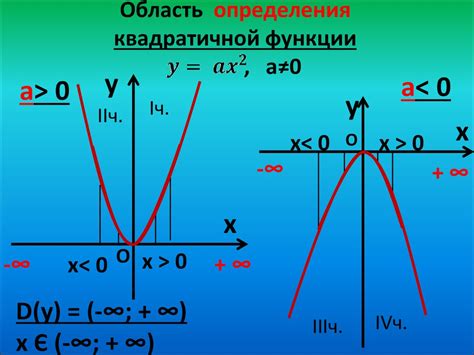
Как найти область определения квадратичной функции?

Чтобы найти область определения квадратичной функции, нужно учесть следующие факты:
- 1. Парабола, заданная квадратичной функцией, имеет смысл и определена для всех действительных значений переменной x.
- 2. Коэффициент a отличен от нуля, иначе функция перестанет быть квадратичной.
Таким образом, область определения квадратичной функции y = ax^2 + bx + c является множеством всех действительных чисел (-∞, +∞).
Примеры поиска области определения квадратичной функции
Пример 1:
Дано уравнение функции f(x) = 2x^2 + 3x - 5. Найдем дискриминант:
D = 3^2 - 4 * 2 * (-5) = 9 + 40 = 49
Так как дискриминант положительный, то у уравнения есть два корня.
Таким образом, область определения данной функции составляет всю числовую прямую.
Пример 2:
Дано уравнение функции f(x) = x^2 - 6x + 9. Найдем дискриминант:
D = (-6)^2 - 4 * 1 * 9 = 36 - 36 = 0
Так как дискриминант равен нулю, то у уравнения есть один корень.
Таким образом, область определения данной функции составляет множество всех действительных чисел.
Пример 1: Область определения квадратичной функции вида y = ax^2 + bx + c
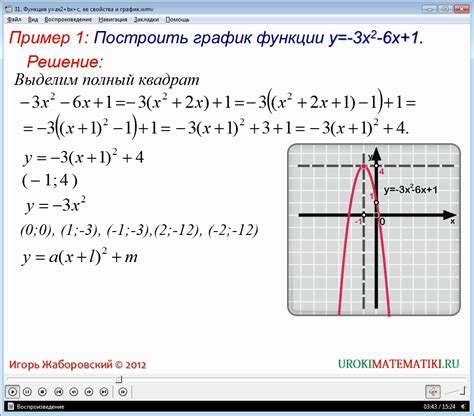
Обратим внимание, что квадратичная функция является полиномом второй степени. Такие функции определены для любого значения x, то есть область определения является множеством всех действительных чисел, обозначаемым как R (выражение "R" означает множество всех действительных чисел).
Исключений нет, поэтому область определения квадратичной функции вида y = ax^2 + bx + c равна R.
Пример 2: Область определения квадратичной функции вида y = a(x - h)^2 + k