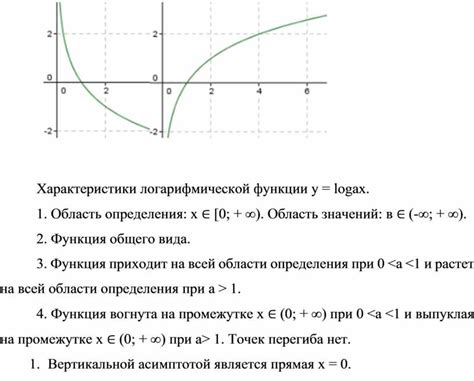
Определение области определения функции является одним из важных этапов изучения математического объекта. Когда речь идет о логарифмической функции, определение ее области определения может быть осуществлено с помощью графика. График логарифмической функции представляет собой кривую, которая может менять свою форму в зависимости от значений аргумента и основания логарифма.
Чтобы определить область определения логарифмической функции по графику, необходимо проанализировать основные характеристики графика. Сначала стоит обратить внимание на присутствие асимптот и точек разрыва. Если график имеет горизонтальные асимптоты, то это указывает на существование точек разрыва в определенных значениях аргумента.
Кроме того, следует проанализировать поведение графика на разных участках. Если функция является непрерывной, то это означает, что ее область определения расположена во всей числовой прямой. Однако, если график имеет точки разрыва, то нужно определить значение аргумента, при котором возникает разрыв.
Анализ графика логарифмической функции
Область определения логарифмической функции зависит от основания логарифма и системы вещественных чисел. В случае, когда логарифм берется по основанию 10 или по основанию е, область определения функции логарифма совпадает с множеством положительных вещественных чисел. Если основание логарифма отличается от 10 и е, то область определения может быть ограничена другими условиями, например, положительностью аргумента.
При анализе графика логарифмической функции необходимо обратить внимание на следующие особенности:
| Особенность | Описание |
|---|---|
| Принадлежность области определения | Необходимо проверить, что все точки на графике логарифмической функции принадлежат области определения данной функции. |
| Наличие асимптот | Асимптоты графика логарифмической функции могут быть горизонтальными и вертикальными. Необходимо определить положение и значения асимптот. |
| Экстремумы | Логарифмическая функция может иметь экстремумы, то есть точки максимума или минимума на графике. Необходимо определить их координаты. |
| Точки разрыва | Логарифмическая функция может иметь точки разрыва, где график функции "ломается". Необходимо определить тип точек разрыва и их координаты. |
Анализ графика логарифмической функции позволяет получить дополнительную информацию о свойствах функции, ее поведении и использовании в различных задачах и приложениях. Используя график, можно увидеть, как функция меняется при изменении аргумента и какие значения она принимает.
Нахождение точек разрыва функции
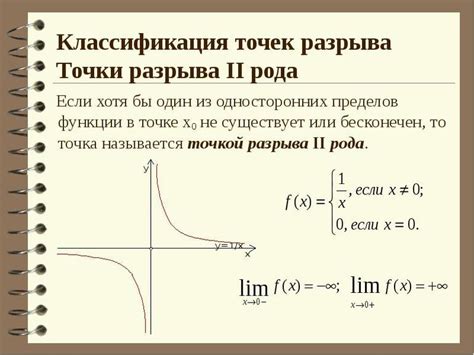
Нахождение точек разрыва функции может быть полезным при изучении ее свойств и характеристик, а также при решении задач и экономических моделей.
Существуют различные виды точек разрыва функции. Одним из распространенных типов является точка разрыва первого рода, при которой функция не определена в определенной точке. Например, для логарифмической функции с основанием больше 1, точкой разрыва будет x=0, так как логарифм не определен для отрицательных чисел и нуля.
Точки разрыва второго рода возникают, когда функция имеет разрыв в своем графике. Например, логарифмическая функция с основанием меньше 1 (0
Для определения точек разрыва можно анализировать график функции и находить значения, при которых функция становится не определенной или имеет разрыв. Это можно сделать, например, при помощи интерактивных графических калькуляторов или математических программ.
При анализе функции также необходимо учитывать особенности самой функции и ее графика. Например, логарифмическая функция с основанием больше 1 не определена для отрицательных чисел, поэтому точкой разрыва будет любое отрицательное значение x.
Точки разрыва функции являются важным аспектом ее изучения, так как они помогают определить область определения функции и понять ее поведение по графику. При анализе функции можно также использовать математические методы и алгоритмы для определения точек разрыва и других характеристик функции.
Определение значений, на которых логарифмическая функция не определена

Логарифмическая функция не определена на отрицательных значениях аргумента и на нуле. Это связано с особенностями определения логарифма.
Если аргумент логарифма является отрицательным числом или равен нулю, то результатом функции будет комплексное число. В математике, комплексный логарифм обладает дополнительными свойствами, и его определение выходит за рамки данной статьи.
Таким образом, для логарифмической функции $y = \log_b(x)$ область определения состоит из всех положительных значений аргумента $x$.
Определение области значений логарифмической функции
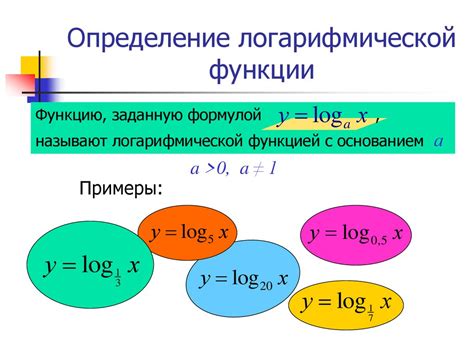
Для логарифмической функции с положительным основанием a и аргументом x область определения определяется следующим образом:
| Основание a | Область определения |
|---|---|
| a > 0, a ≠ 1 | x > 0 |
| a > 1 | x ≠ 0 |
| a = 1 | aргумент не имеет значения |
| a | логарифм не определен |
Таким образом, если в аргументе логарифмической функции встречается 0 или отрицательное число, то функция не определена в этой точке и область определения будет ограничена только положительными значениями аргумента.
Зная область определения логарифмической функции, можно по графику определить область значений – множество всех возможных значений функции. В зависимости от основания и свойств функции, область значений может быть больше нуля или меньше нуля, являться убывающей или возрастающей последовательностью чисел.
Использование графика для проверки области определения
Область определения логарифмической функции можно проверить, используя график этой функции. График логарифмической функции представляет собой кривую линию, которая может иметь различные формы в зависимости от значения базы логарифма и константы сдвига.
Чтобы определить область определения, необходимо исследовать график на наличие различных особенностей:
- 1. Исключительные значения: на графике может быть видно, что функция не определена в некоторых точках. Например, база логарифма должна быть положительным числом и не равной 1. Если в точке графика функция не определена, значит, в этой точке нет области определения.
- 2. Вертикальная асимптота: иногда на графике можно увидеть вертикальную линию, которая указывает на то, что функция стремится к бесконечности (положительной или отрицательной) при приближении к этой точке. Это может сигнализировать о том, что в этой точке нет области определения.
- 3. Горизонтальная асимптота: если на графике есть горизонтальная линия, которая горизонтально расположена вверху или внизу от оси x, это может означать, что функция стремится к определенному значению при стремлении аргумента к бесконечности. Это может указывать на ограничение области определения.
- 4. Монотонность: функция может быть возрастающей или убывающей на определенном интервале значений. Такие интервалы могут подтверждать наличие или отсутствие области определения.
Анализируя эти особенности графика, можно определить область определения логарифмической функции. Однако следует помнить, что использование графика может быть лишь вспомогательным методом и не всегда позволяет точно определить область определения. Для более точного определения области определения логарифмической функции рекомендуется использовать аналитический подход и математические операции.