Область определения степенной функции является одним из наиболее важных понятий в алгебре. Она определяет все значения, которые может принимать функция. Для того чтобы найти область определения степенной функции, необходимо учитывать условия, ограничения и свойства функции.
Методы анализа позволяют легко определить область определения степенной функции. Сначала следует определить, какие значения могут принимать аргументы функции. В случае степенной функции вида y = x^n, аргумент должен быть положительным числом, так как отрицательные значения не определены для натуральных степеней. Также нужно учесть условия, которые могут ограничивать область определения, например, в случае функции с радикалами.
Другой способ определения области определения степенной функции – это анализ графика функции. Построение графика функции позволяет визуализировать значения, которые функция может принимать. График степенной функции может иметь различные формы – возрастающую, убывающую, стремящуюся к нулю и т.д. На основе графика можно определить, какие значения аргумента и функции являются допустимыми. Исключениями являются функции с отрицательными показателями степени, так как они имеют ограниченную область определения.
Как найти область определения степенной функции

Область определения степенной функции определяется набором значений, для которых функция имеет смысл. Для задачи поиска области определения степенной функции с показателем n, следует учесть два важных аспекта:
- Показатель степени: в степенной функции y = x^n важно учесть значения показателя степени. Если показатель степени n является натуральным числом, то функция определена для всех действительных значений x. Если показатель степени n является рациональным числом, то следует учесть условия для определенных значений x, чтобы избежать деления на ноль.
- Ограничения на значения аргумента: в степенной функции y = x^n особое внимание следует уделить значениям аргумента x. Если показатель степени n является четным, то функция определена для всех действительных значений x. Если показатель степени n является нечетным, то функция определена для всех действительных значений x.
Определение области определения степенной функции можно обобщить следующим образом:
- Если показатель степени n является натуральным числом, то область определения функции равна множеству всех действительных чисел.
- Если показатель степени n является рациональным числом и нечетным, то область определения функции равна множеству всех действительных чисел.
- Если показатель степени n является рациональным числом и четным, то область определения функции равна множеству всех действительных чисел, за исключением значения x = 0 (так как деление на ноль неопределено).
Важно помнить, что каждая степенная функция имеет свою область определения, и она может изменяться в зависимости от значения показателя степени и ограничений на значения аргумента.
Методы анализа для 9 класса
Область определения степенной функции определяет множество всех значений, которые может принимать аргумент функции. Для того чтобы найти область определения, необходимо учитывать ограничения, которые могут возникать в различных случаях.
Если степенная функция имеет вид f(x) = x^n, где n - натуральное число, то ее область определения состоит из всех действительных чисел.
Однако, если в степени n стоит иррациональное число, то область определения может быть ограничена. Например, для функции f(x) = \sqrt{x} область определения будет состоять из всех неотрицательных действительных чисел, так как нельзя извлекать корень из отрицательного числа.
Также, область определения степенной функции может быть ограничена в случае, когда в знаменателе стоит степень с отрицательным показателем. Например, для функции f(x) = \frac{1}{x^n} область определения будет состоять из всех действительных чисел, кроме нуля, так как нельзя делить на ноль.
Умение анализировать область определения степенной функции позволяет ученикам правильно решать задачи и избегать ошибок при нахождении значений функции в определенных точках. Благодаря данному анализу, ученики получают навыки критического мышления и развивают математическую логику.
Шаг 1: Изучение понятия степенной функции

Показатель степени n может быть как положительным, так и отрицательным числом. Если n – целое положительное число, то степенная функция будет монотонно возрастать или убывать в зависимости от значения a и n. Если n – отрицательное число, то степенная функция может быть неопределена при некоторых значениях переменной x.
Изучение понятия степенной функции позволит нам лучше понять, как определить ее область определения и применять соответствующие методы анализа. Переходим к следующему шагу – определению области определения степенной функции.
Что такое степенная функция и ее свойства
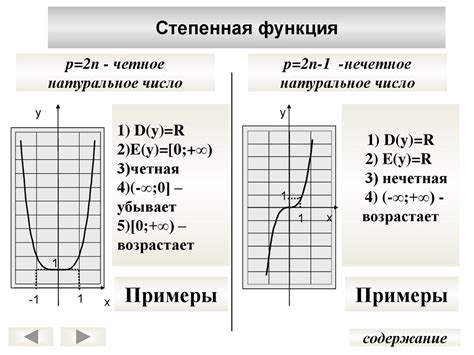
Главной особенностью степенной функции является возведение в степень переменной. Коэффициент a называется коэффициентом пропорциональности, а показатель степени n определяет изменение кривой графика функции.
Свойства степенной функции:
- Нечетность или четность функции зависит от значения показателя степени n. Если n - нечетное число, то функция нечётная. Если n - четное число, то функция чётная.
- Областью определения степенной функции является множество всех действительных чисел, за исключением значения 0 в случае, когда n – натуральное число.
- Если показатель степени n - положительное число, то график функции при x → ±∞ стремится к +∞. Если n - отрицательное число, то график функции при x → ±∞ стремится к 0.
- Если коэффициент пропорциональности a - положительное число, то график функции с "положительной" степенью открывается вверх. Если a - отрицательное число, то график функции с "отрицательной" степенью открывается вниз.
Шаг 2: Определение области определения

Чтобы определить область определения степенной функции, необходимо учесть несколько факторов:
- Если показатель степени n является положительным целым числом, то функция определена для любого значения основания x. Это означает, что нет ограничений на значения x и функция определена на всей числовой прямой.
- Если показатель степени n равен нулю, то функция определена для всех значений основания x, за исключением нуля. В этом случае область определения функции не включает ноль.
- Если показатель степени n является отрицательным целым числом, то функция определена для всех значений основания x, за исключением нуля. В этом случае область определения функции также не включает ноль.
- Если показатель степени n является дробным числом, то функция определена для всех значений основания x, за исключением нуля, и отрицательных чисел, если знаменатель дроби является нечетным числом.
Таким образом, чтобы найти область определения степенной функции, необходимо учитывать значения показателя степени n и учитывать, что функция не определена при нулевых значениях основания x и, возможно, при некоторых отрицательных значениях основания.
| Форма функции | Область определения |
|---|---|
| y = x^n | Для x ≠ 0 |
| y = x^0 | Для x ≠ 0 |
| y = x^(-n) | Для x ≠ 0 |
| y = x^(m/n) | Для x > 0, если n - нечетное |
Как найти область определения степенной функции

Основание степенной функции не может быть отрицательным числом, если показатель степени является рациональным числом с нечетным знаменателем. Также при наличии корня в основании, необходимо учитывать ограничения, связанные с типом корня (например, квадратный корень из отрицательного числа).
Показатель степени должен быть определен, то есть не может быть отрицательным числом, если основание является отрицательным числом. Также необходимо учесть ситуацию, когда показатель степени является дробным числом и имеет нечетный знаменатель.
Если степенная функция содержит в себе более сложные выражения, необходимо учитывать область определения каждого из этих выражений и применять соответствующие правила для нахождения области определения степенной функции в целом.
Важно отметить, что область определения степенной функции может быть изменена, если функция претерпевает преобразования, такие как смещение, растяжение или сжатие по горизонтали.
Для наглядного представления области определения степенной функции можно построить ее график на координатной плоскости и определить все значения, для которых функция определена.
Итак, для нахождения области определения степенной функции необходимо анализировать основание и показатель степени, учитывать ограничения, связанные с ними, и учесть возможные преобразования функции.
Шаг 3: Методы анализа степенной функции

После нахождения области определения степенной функции в степени с положительным показателем, процесс анализа может продолжаться с использованием различных методов.
1. Графический метод: Для анализа степенной функции можно построить её график на координатной плоскости. График степенной функции с положительным показателем имеет вид параболы, которая может быть выпуклой вверх или вниз в зависимости от значения показателя. Из графика можно определить такие характеристики функции, как экстремумы, возрастание или убывание функции.
2. Аналитический метод: При анализе степенной функции можно использовать аналитические методы, такие как нахождение производной функции, нахождение точек пересечения с осями координат и составление таблицы значений функции. Нахождение производной позволяет определить характер функции: его возрастание или убывание, нахождение экстремумов и точек перегиба.
3. Неравенство между числами: Для нахождения области определения степенной функции можно использовать неравенства между числами. Например, если показатель степенной функции является нечетным, то функция будет определена на всей числовой прямой. В случае, если показатель является четным, функция будет определена только на неположительных числах, так как отрицательные числа, возведенные в четную степень, дают положительные результаты.
4. Таблица значений: Составление таблицы значений функции позволяет наглядно представить значения функции при различных значениях аргумента. Таблицу можно составить, выбирая значения аргумента из области определения функции и находя соответствующие значения функции. Для степенных функций с положительным показателем, значения функции будут положительными, если аргумент положительный, и могут быть нулевыми при значении аргумента равном нулю.
| Аргумент | Значение функции |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
С помощью этих методов можно получить больше информации о степенной функции, такой как её поведение на промежутках, экстремумы, точки перегиба и другие характеристики.