Определение области определения уравнения - это один из важных шагов в решении задач и проблем, связанных с математикой. В особенности, в 8 классе, когда знания ребенка начинают расширяться и возрастает сложность задач. Область определения - это множество всех значений переменной, при которых уравнение имеет смысл.

Для определения области определения уравнения, необходимо выяснить, для каких значений переменной уравнение имеет смысл и не содержит деления на ноль или корней, не является отрицательным подкоренным выражением и т.п. Это может быть довольно сложной задачей, особенно, если в уравнении присутствуют различные функции, операторы и прочие математические символы.

Определение области определения может быть представлено в виде числового интервала на прямой или множества чисел. Для этого можно использовать математическую нотацию или показать на числовой оси. Например, для уравнения sqrt(x-5) + 2x = 7, область определения может быть представлена так: D = {x ∈ R: x ≥ 5}.

Как найти область определения уравнения в 8 классе

Чтобы найти область определения уравнения, нужно учесть ограничения, которые могут существовать для переменных в уравнении. Правила для определения области определения различаются в зависимости от типа уравнения.

Для уравнений с обыкновенными числами и алгебраическими выражениями, область определения определяется так:

1. Определите все значения, при которых знаменатель в уравнении не равен нулю. Нулевой знаменатель может привести к делению на ноль, что является недопустимым в математике.
2. Учтите любые другие ограничения, указанные в условии задачи. Например, если переменная должна быть положительной, отрицательной или не может быть нулем, то данные ограничения также должны быть учтены в определении области определения.

Для уравнений с функциями, такими как квадратные функции, логарифмические функции или тригонометрические функции, область определения может быть более сложной. В этих случаях рекомендуется использовать специальные правила и свойства, связанные с каждым типом функции.

Важно помнить, что область определения может быть различной для разных переменных в одном уравнении. Поэтому важно учитывать все ограничения для каждой переменной, чтобы правильно определить область определения уравнения.

Понятие области определения

Для определения области определения уравнения необходимо учесть все ограничения и условия, которые могут влиять на его значения.

Основные правила для определения области определения:

1. Ограничения известных величин: например, корень из отрицательного числа в действительных числах не определен.
2. Знаменатель не может быть равен нулю, поэтому нужно исключить те значения переменной, при которых знаменатель обращается в ноль.
3. Ограничения на подкоренное выражение: например, в выражении √(x - 5) значение x должно быть не меньше 5.

Область определения может быть представлена в виде интервалов или в виде множества чисел.

Определение области определения позволяет избегать ошибок при решении уравнений и функций и обеспечивает корректность их дальнейшей работы.

Способы определения области определения

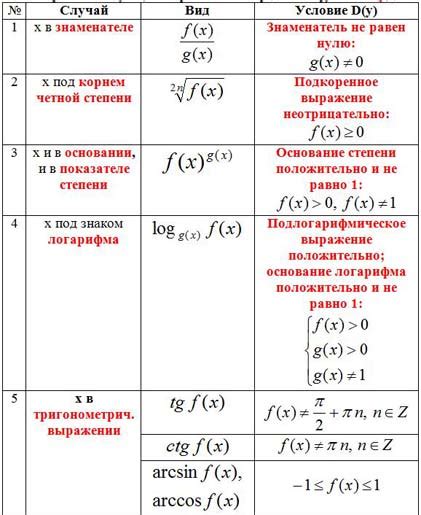
Для определения области определения уравнения можно использовать несколько способов:

1. Анализ выражений в уравнении. Если в уравнении нет никаких ограничений на аргумент, то его область определения будет состоять из всех допустимых значений данного аргумента.
2. Учет возможных делений на ноль или корней с отрицательным радикалом. Если в уравнении есть деление на переменную или корень из переменной, необходимо исключить значения аргумента, при которых это происходит.
3. Анализ знаменателя в уравнении. Если в уравнении есть знаменатель, который должен быть отличен от нуля, необходимо исключить значения аргумента, при которых его знаменатель равен нулю.
4. Ограничения на аргумент, заданные в условии задачи. Иногда в условии задачи заданы определенные ограничения на значения аргумента, и область определения будет состоять только из значений, удовлетворяющих этим ограничениям.

Определение области определения уравнения важно для правильного решения уравнений и понимания их смысла. При анализе уравнений необходимо учитывать все условия, ограничения и особенности каждого конкретного уравнения.