Определение области значения функции – важный шаг при анализе графиков функций. Областью значения функции называют множество всех возможных значений, которые может принимать функция. Если мы понимаем, что на графике функции нет определенных ограничений, то определение области значения становится еще более важным.
Чтобы определить область значения функции по графику, следует внимательно изучить график функции и пронаблюдать все его особенности. Начните с определения экстремумов – точек, в которых функция принимает максимальные и минимальные значения. Затем положите в свои наибольшие и наименьшие значения функции, отметив их на графике. Это поможет определить границы области значения функции.
Важно помнить, что областью значения функции не является сам график, а лишь множество всех значений, которые может принимать функция. Это значит, что некоторые значения могут быть недостижимы на графике функции, но они все равно входят в ее область значения. Кроме того, областью значения функции может быть как конечное множество значений, так и бесконечное множество. Это зависит от поведения функции на протяжении всего интервала определения.
Понятие области значений функции

Областью значений функции называется множество всех возможных значений, которые может принимать функция на своем области определения. Иными словами, это множество значений, которые можно получить, подставляя различные значения аргументов функции.
График функции, помимо отображения ее изменения в пространстве, также позволяет нам определить область значений функции. Для этого необходимо изучить вертикальные отрезки на графике, а именно, все значения функции, которые она принимает на данном отрезке.
Обычно, чтобы определить область значений функции, рассматривают все значения y на оси ординат, которые можно прочитать с графика. Эти значения образуют искомую область значений функции.
Однако стоит отметить, что график может быть ограничен сверху или снизу, и в таком случае область значений также будет ограничена. Также может быть случай, когда график функции состоит из нескольких разрозненных кусков или принимает только определенные значения на заданном интервале. В таких случаях областью значений будет соответствующий отрезок или набор этих значений.
Важно помнить, что область значений функции необходимо определять с учетом ее области определения, поскольку некоторые значения аргумента могут быть запрещены или неопределены для функции.
Методы определения области значения функции по графику
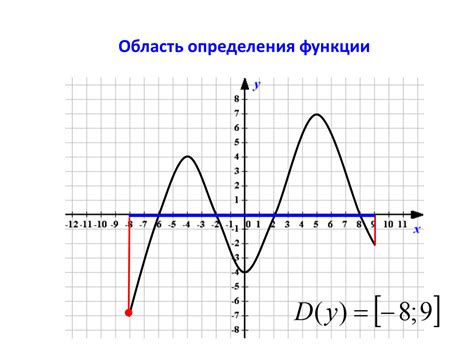
Существуют несколько методов, которые помогают определить область значения функции по графику:
| Метод | Описание |
|---|---|
| Наблюдение за возрастанием/убыванием | Если график функции возрастает на протяжении всего промежутка, то область значений будет положительными числами. Если график функции убывает на протяжении всего промежутка, то область значений будет отрицательными числами. Если график функции и возрастает, и убывает, то область значений будет включать в себя все вещественные числа. |
| Анализ точек экстремума | Если на графике функции есть точка минимума, то минимальное значение будет входить в область значений. Если на графике функции есть точка максимума, то максимальное значение будет входить в область значений. Если таких точек нет, то область значений будет включать в себя все вещественные числа. |
| Изучение асимптот | Асимптоты графика функции помогают определить ограничения для области значений. Например, если график функции имеет горизонтальную асимптоту, то область значений будет ограничена данным горизонтальным уровнем. Если график функции имеет вертикальную асимптоту, то область значений будет ограничена данным вертикальным уровнем. |
Использование графика функции для определения области значений является важным навыком в анализе функций. Этот метод позволяет визуализировать и лучше понять возможные значения функции на заданных интервалах.
Метод прямых линий
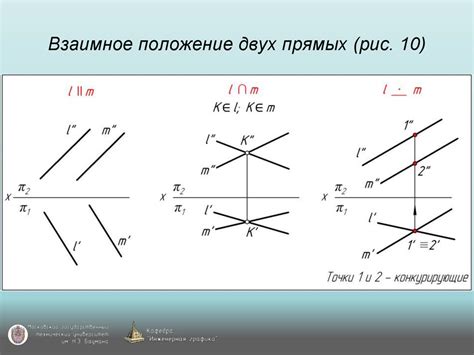
Чтобы применить метод прямых линий, нужно выбрать две точки на графике, через которые можно провести прямую линию. Используя эти точки, можно определить наклон прямой и ее положение относительно оси абсцисс.
Если прямая имеет положительный наклон и находится выше оси абсцисс, то это означает, что значения функции относятся к положительным числам. Если прямая имеет положительный наклон и находится ниже оси абсцисс, то значения функции отрицательные. Аналогично, прямые с отрицательным наклоном и положением выше оси абсцисс указывают на отрицательные значения функции, а под осью абсцисс – на положительные.
Если прямая является горизонтальной, то это означает, что функция имеет постоянное значение на данном участке графика. Если прямая вертикальна, значит, функция неопределена в данной точке.
Таким образом, метод прямых линий позволяет определить область значений функции по графику, основываясь на анализе наклона и положения прямых линий, проведенных на графике функции.
Метод табличного задания функции
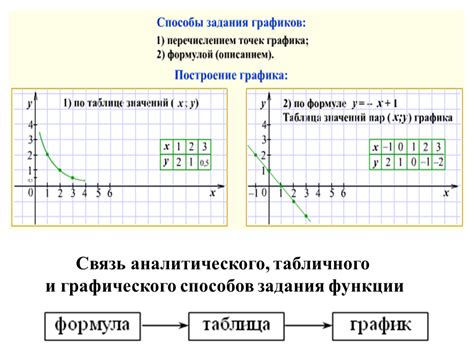
Для того чтобы построить таблицу значений функции, мы выбираем некоторые значения аргумента и подставляем их в функцию, вычисляя соответствующие значения функции. В итоге получаем пары значений аргумента и функции, которые заносим в таблицу.
Затем, используя полученные значения, строим график функции на координатной плоскости. При этом, если у нас есть некоторое ограничение на значения аргумента (например, задан диапазон), то мы строим график только для значений аргумента, удовлетворяющих этому ограничению.
Для определения области значений функции по графику, мы исследуем значения функции на графике и находим наименьшее и наибольшее значение, которые она принимает. Таким образом, получаем интервал значений функции, который является её областью значений.
Если функция задана явной формулой, то метод табличного задания является дополнительным способом проверки правильности построения графика и определения области значения функции.
Метод табличного задания функции позволяет наглядно представить область значений функции по её графику и является одним из важных инструментов в изучении функций и их свойств.
Метод проверки точек
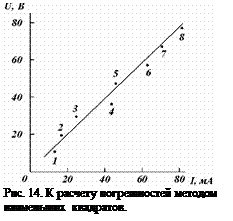
Для начала необходимо выбрать несколько точек на графике функции. Разумным выбором является выбор точек из разных областей графика - начала, середины и конца.
После выбора точек необходимо подставить их значения в функцию и проанализировать результат. Если полученные значения удовлетворяют условиям функции, то эти точки принадлежат области значений функции. В противном случае, точки не принадлежат области значения.
При использовании метода проверки точек рекомендуется выбирать как можно больше точек для анализа, чтобы получить более точный результат. Также стоит учитывать особенности функции, например, наличие асимптот или разрывов, что может повлиять на область значений.
Применение данного метода не требует сложных математических выкладок и подходит для определения области значений функций в 10 классе. Однако, следует помнить, что метод проверки точек основан на эмпирическом анализе и не всегда дает точный результат. Поэтому его результаты следует дополнять другими методами и проверять на большем количестве точек.
| Пример | Точка | Значение | Принадлежность |
|---|---|---|---|
| 1 | x = -2 | f(-2) = 5 | Принадлежит |
| 2 | x = 0 | f(0) = 3 | Принадлежит |
| 3 | x = 2 | f(2) = -1 | Не принадлежит |
В данном примере точки 1 и 2 принадлежат области значений функции, а точка 3 не принадлежит.
Метод экстремумов
Для определения точек экстремума необходимо найти значения x, при которых производная функции равна нулю или не существует. Это моменты, когда функция меняет свое поведение и может достигать максимума или минимума.
Как правило, для применения метода экстремумов необходимо знать аналитическую формулу функции. Однако, даже при наличии только графика функции, можно примерно определить точки экстремума.
Для этого нужно провести вертикальные прямые, перпендикулярные оси ординат, через каждую точку возможного экстремума. Если прямая пересекает график функции, то в этой точке функция достигает экстремума. Если прямая не пересекает график, то в данной точке экстремума нет.
При определении области значений функции методом экстремумов необходимо учитывать, что функция может иметь несколько экстремумов на заданном интервале или не иметь их вовсе. Также возможны случаи, когда область значений функции не ограничена.
Метод экстремумов является простым и эффективным способом определения области значений функции по ее графику. Однако, его применение требует некоторых предварительных знаний и наблюдательности при анализе графика функции.
Метод интервалов монотонности

Для применения этого метода необходимо проанализировать график функции и выявить интервалы, на которых функция возрастает или убывает.
Если на интервале функция возрастает, то это значит, что значения функции на этом интервале увеличиваются с увеличением аргумента. В таком случае, область значений функции будет представлена всеми положительными значениями, принимаемыми функцией на данном интервале.
Если на интервале функция убывает, то это значит, что значения функции на этом интервале уменьшаются с увеличением аргумента. В таком случае, область значений функции будет представлена всеми отрицательными значениями, принимаемыми функцией на данном интервале.
Чтобы определить область значений функции, необходимо найти все интервалы возрастания и убывания, и затем объединить все соответствующие области значений в одну.
Например, если график функции возрастает на интервале (-∞, a) и убывает на интервале (b, +∞), то область значений функции будет представлена всеми значениями, принимаемыми функцией на интервалах (a, b).
Метод интервалов монотонности является одним из основных методов, которые позволяют определить область значений функции по ее графику в 10 классе.