Определение общей величины множества является важной задачей во многих областях науки и повседневной жизни. Независимо от того, являетесь ли вы математиком, экономистом или просто пытаетесь разобраться в своих повседневных расходах, знание того, как определить общую величину множества, поможет вам принимать взвешенные решения и анализировать данные.
Основной способ определения общей величины множества - суммирование элементов этого множества. Если множество состоит из чисел, то для определения общей величины достаточно просто просуммировать все числа. Однако в реальной жизни множество может быть более сложным и включать в себя различные объекты или категории.
Для определения общей величины таких множеств можно использовать агрегирующие функции, такие как сумма, среднее значение, максимум или минимум. Эти функции позволяют сгруппировать и анализировать данные с различных уровней иерархии. Например, если у вас есть множество товаров с различными ценами, вы можете определить общую стоимость всех товаров или среднюю стоимость товара в этом множестве. Эти значения помогут вам оценить свои расходы и принять решение на основе этих данных.
Величина множества: что это такое?

Величина множества может быть определена как конечная, то есть иметь определенное число элементов, или как бесконечная, если количество элементов неограничено.
Для обозначения величины множества обычно используется символ "n". Например, если есть множество A, в котором содержится 5 элементов, то величина этого множества будет обозначаться следующим образом: n(A) = 5.
Пример:
Рассмотрим множество X, которое содержит элементы {1, 2, 3}. В данном случае величина множества будет равна 3, так как в множестве X содержатся три элемента.
Основные понятия и определения в теории множеств

Элементы - это индивидуальные объекты или концепции, которые составляют множество. Элементы множества могут быть представлены числами, буквами, символами или другими объектами в зависимости от контекста.
Пересечение - это операция, которая возвращает множество, содержащее только те элементы, которые присутствуют одновременно как в первом, так и во втором множестве. Записывается в виде символа знака "пересечение" (∩).
Объединение - это операция, которая возвращает множество, содержащее все элементы из обоих множеств. Записывается в виде символа знака "объединение" (∪).
Разность - это операция, которая возвращает множество, содержащее элементы, присутствующие только в первом множестве, но не во втором. Записывается в виде символа знака "разность" (\\ или \).
Декартово произведение - это операция, которая строит множество, состоящее из всех возможных упорядоченных пар элементов из двух множеств. Записывается в виде символа знака "декартово произведение" (×).
Как определить мощность конечного множества

1. Счетчик. Простейший способ определить мощность множества – посчитать количество его элементов. Для этого необходимо последовательно перебрать все элементы множества и увеличивать счетчик на 1 для каждого элемента.
2. Математическая формула. Если известно, что множество содержит элементы в определенном диапазоне, то можно использовать математическую формулу для определения мощности множества. Например, если множество содержит все натуральные числа от 1 до 10, то его мощность равна 10.
3. Равномощность с известным множеством. Если имеется два конечных множества, и известно, что они равномощны, то можно определить мощность одного множества, зная мощность другого. Например, если одно множество содержит 5 элементов, а другое множество равномощно ему, то мощность второго множества также будет 5.
4. Диаграмма Эйлера. Диаграмма Эйлера помогает визуально определить мощность конечного множества. Для этого необходимо изобразить множества в виде пересекающихся кругов, причем каждый круг представляет собой одно множество, а пересечение кругов – общие элементы. По размеру пересечения можно определить мощность общих элементов.
Используя эти методы, можно легко определить мощность конечного множества. Знание мощности множества позволяет более точно анализировать данные и выполнять различные математические операции над ними.
Способы вычисления общей величины бесконечных множеств

2. Метод сравнения по характеристической функции. Характеристическая функция множества позволяет определить, принадлежит ли элемент множеству или нет. Сравнение характеристических функций может помочь выявить различия в общей величине бесконечных множеств. Если одно множество имеет более сложную или разнообразную характеристическую функцию, это может свидетельствовать о его большей общей величине.
Комбинируя эти и другие методы, исследователи могут определить общую величину бесконечных множеств и сравнить их между собой. Однако, следует отметить, что вопрос общей величины бесконечных множеств остается открытым и подлежит дальнейшим исследованиям.
Пример вычисления мощности множества чисел или отрезков

Пример 1: Вычисление мощности множества чисел
Пусть дано множество чисел A = {1, 2, 3, 4, 5}. Чтобы найти мощность этого множества, нужно посчитать количество элементов в нем. В данном случае множество A содержит 5 элементов, поэтому его мощность равна 5.
Пример 2: Вычисление мощности множества отрезков
Пусть дано множество отрезков B = {[0, 1], [1, 2], [2, 3], [3, 4]}. Отрезки – это пары чисел, где первое число обозначает начало отрезка, а второе – его конец. Чтобы найти мощность множества отрезков, нужно посчитать количество отрезков в нем. В данном случае множество B содержит 4 отрезка, поэтому его мощность равна 4.
Таким образом, для вычисления мощности множества чисел или отрезков необходимо посчитать количество элементов в данном множестве.
Критерии равномощности множеств
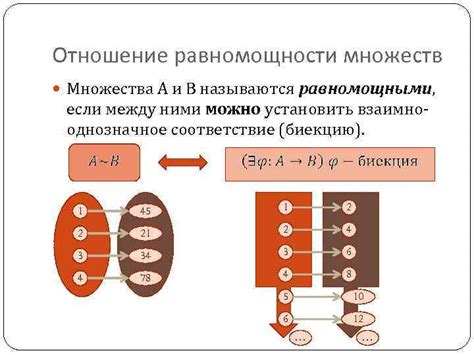
Для определения равномощности множеств необходимо выполнять следующие критерии:
1. Критерий однозначного соответствия: Если можно установить однозначное соответствие между элементами двух множеств, то эти множества равномощны. Например, если каждому элементу множества A можно сопоставить ровно один элемент множества B, и наоборот, то A и B равномощны.
2. Критерий инъективного отображения: Если существует инъективное (неукладывающееся) отображение множества A в множество B, то A имеет мощность, не превышающую мощность множества B.
3. Критерий сюръективного отображения: Если существует сюръективное (перекрывающееся) отображение множества A на множество B, то A имеет мощность, не меньшую мощности множества B.
4. Критерий биективного отображения: Если существует биективное (взаимнооднозначное) отображение множества A на множество B, то A и B равномощны. То есть между каждым элементом из A и каждым элементом из B устанавливается однозначное соответствие.
Таким образом, для определения равномощности множеств можно использовать различные критерии, позволяющие установить соответствие между элементами этих множеств и выяснить их общую величину.
Практическое применение теории множеств

Одним из примеров практического применения теории множеств является решение задач по управлению базами данных. Множества могут быть использованы для описания множества элементов в базе данных и их взаимосвязи. Операции с объединением, пересечением и разностью множеств позволяют удобно работать с данными и проводить операции по их обновлению и манипуляции.
Теория множеств также находит применение в анализе и обработке данных. Множество может представлять собой набор объектов или событий, а операции над множествами могут быть использованы для классификации данных, поиска сходств и выборки нужных элементов. Например, при анализе текстов множества могут использоваться для представления уникальных слов или букв.
Кроме того, теория множеств применяется в криптографии. Операции над множествами могут быть использованы для выполнения шифрования и дешифрования данных, а также для проверки целостности и подлинности информации.