Окружность - одна из самых основных геометрических фигур, которую мы изучаем еще на начальных уроках математики. Ее полный оборот равен 360 градусам, и она обладает свойством равности всех своих радиусов.
Но когда нам необходимо вычислить площадь окружности или длину ее окружности, мы обращаемся к геометрическим формулам. Например, есть формула, позволяющая найти площадь окружности по радиусу. Но как определить саму окружность по заданному радиусу? В этом случае нам помогут калькуляторы и математические формулы.
Простым способом определить окружность по радиусу является использование математической формулы, которая гласит, что длина окружности равна произведению числа пи (π) на удвоенное значение радиуса (r). Другими словами, формула имеет вид - L = 2πr. Все, что вам нужно сделать - вычислить произведение числа пи на значение радиуса и умножить его на 2. Например, если радиус окружности равен 5 единицам, то длина окружности будет равна 10π единицам.
Что такое окружность: определение и особенности

Еще одной особенностью окружности является то, что любая прямая линия, проходящая через центр окружности, будет являться диаметром. Диаметр - это отрезок, соединяющий две противоположные точки на окружности и проходящий через ее центр.
Окружность также имеет понятие длины окружности, которая определяется формулой:
Длина окружности = 2πR,
где R - радиус окружности, а π (пи) - математическая константа, приближенное значение которой равно 3,14.
Кроме того, окружность имеет понятие площади, которая определяется формулой:
Площадь окружности = πR².
| Параметр | Описание |
|---|---|
| Центр окружности | Точка, от которой все точки окружности равноудалены |
| Радиус окружности | Расстояние от центра до любой точки на окружности |
| Диаметр окружности | Отрезок, соединяющий две противоположные точки на окружности через ее центр |
| Длина окружности | Общая длина окружности |
| Площадь окружности | Площадь, ограниченная окружностью |
Радиус окружности и его значение

Значение радиуса оказывает существенное влияние на свойства окружности. Он влияет на длину окружности, площадь и диаметр фигуры.
Радиус окружности может быть как положительным, так и отрицательным числом. Его значение всегда является абсолютным, не зависит от направления и всегда рассчитывается от центра.
Чтобы узнать указанное значение радиуса, достаточно поделить диаметр окружности на 2 или известную площадь на удвоенное значение числа Pi. Также, радиус можно выразить через длину окружности, разделив ее на 2*Pi.
Формула для расчета радиуса:
Радиус = Диаметр / 2
Радиус = √(Площадь / Пи)
Радиус = Длина окружности / (2 * Пи)
Пользуясь этими формулами, можно легко определить значение радиуса окружности и далее приступить к решению других геометрических задач, связанных с этим параметром.
Формула для определения окружности по радиусу
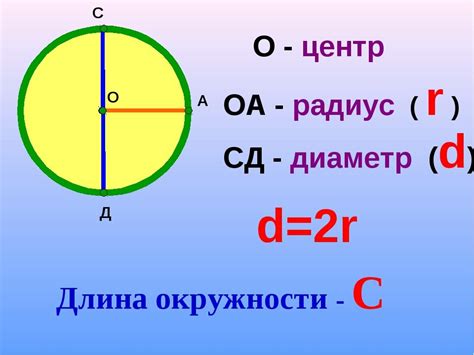
| Формула: | C = 2πr |
|---|---|
| Где: |
|
Данная формула позволяет вычислить длину окружности по заданному радиусу. Для этого необходимо умножить значение радиуса на 2π.
Например, если радиус окружности равен 5 единицам, то длина окружности будет равна:
C = 2π * 5 = 10π единиц.
Таким образом, используя данную формулу, можно определить длину окружности по заданному радиусу и использовать полученное значение для решения различных задач и задач геометрии.
Как рассчитать длину окружности по радиусу

Формула для расчета длины окружности по радиусу задается следующим образом:
Длина окружности = 2πr
Где π – это математическая константа, приближенное значение которой равно 3,14159, а r – радиус окружности.
Для примера, рассчитаем длину окружности с радиусом 5 единиц:
Длина окружности = 2π × 5 = 31,4159 единиц
Таким образом, длина окружности с радиусом 5 единиц равна примерно 31,4159 единиц.
Теперь, когда вы знаете формулу для расчета длины окружности по радиусу, вы можете легко определить этот параметр для любой окружности, используя калькулятор или ручной расчет.
Как найти площадь окружности по радиусу
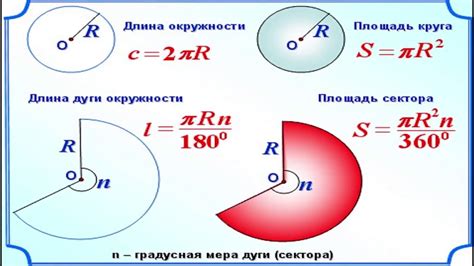
Площадь окружности может быть найдена по формуле:
S = π * r2
где:
S - площадь окружности;
π (пи) - математическая константа, примерно равная 3,14159;
r - радиус окружности.
Чтобы найти площадь окружности по заданному радиусу, нужно возвести радиус в квадрат и умножить на число π.
Например, если радиус окружности равен 5 сантиметрам, то площадь будет:
S = 3,14159 * 52 = 3,14159 * 25 = 78,54 сантиметра квадратного.
Найденная площадь окружности по радиусу поможет вам решить различные задачи, связанные с геометрией или физикой. Она может быть использована, например, для расчета площади круглого участка земли, или для определения площади круглого объекта.
Окружность и другие геометрические фигуры: что их отличает

Окружность - это замкнутая кривая, все точки которой равноудалены от одной точки, называемой центром окружности. Основная характеристика окружности - это радиус, который определяется как расстояние от центра окружности до любой ее точки. Радиус является основным параметром для определения окружности и используется при расчете ее площади и длины.
В отличие от окружности, другие геометрические фигуры имеют свои уникальные характеристики. Например, треугольник - это фигура, состоящая из трех отрезков, называемых сторонами, и трех точек пересечения сторон, называемых вершинами. Треугольники могут быть разного вида в зависимости от количества и длины сторон, а также углов между ними.
Прямоугольник - это четырехугольник, у которого все углы являются прямыми. Прямоугольник имеет две параллельные стороны, которые также являются равными по длине, и две другие пары сторон, также параллельные друг другу.
Круг - это фигура, которая также имеет радиус, но в отличие от окружности, у круга есть внутренняя площадь. Круг является более сложной фигурой, чем окружность, и его площадь можно вычислить, используя формулу площади круга.
Таким образом, окружность и другие геометрические фигуры имеют свои собственные характеристики и особенности, которые определяются их формой и размерами. Каждая из этих фигур имеет свои уникальные свойства, которые могут быть использованы для решения разнообразных задач и проблем в математике и физике.
Как использовать калькулятор для определения окружности по радиусу
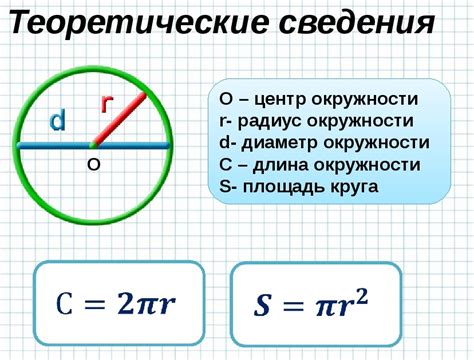
Для использования калькулятора для определения окружности по радиусу вам понадобится:
- Открыть калькулятор на вашем устройстве или воспользоваться онлайн-калькулятором.
- Ввести значение радиуса окружности в соответствующее поле калькулятора.
- Нажать кнопку "Рассчитать" или аналогичную кнопку на калькуляторе.
Калькулятор автоматически выполнит расчет и покажет вам длину окружности в соответствующем поле или выведет результат на экран.
Если у вас нет доступа к калькулятору, вы можете воспользоваться формулой для расчета длины окружности по радиусу. Формула для расчета окружности по радиусу выглядит следующим образом:
Длина окружности = 2 * π * Радиус
Где π (пи) - математическая константа, приближенное значение которой составляет около 3.14.
Чтобы применить эту формулу, нужно умножить значение радиуса на два и на число π. Полученный результат будет являться длиной окружности.
Теперь вы знаете, как использовать калькулятор или формулу для определения длины окружности по радиусу. Этот навык может быть полезен в различных сферах, включая геометрию, строительство и инженерию.
Окружность и ее применение в реальной жизни

В архитектуре окружность используется для создания куполов или круглых витражей. Окружности также применяются при проектировании дорожных развязок и круговых перекрестков, где они помогают обеспечить правильное движение транспорта.
Окружности играют важную роль в оптике. Линзы, такие как линза в фотокамере или в очках, имеют форму окружности или сегмента окружности. Это позволяет изменять фокусное расстояние и корректировать зрение.
Также окружности можно найти в музыкальной области. Граммофонные пластинки и диски имеют форму окружности, по которой воспроизводится звук или записывается информация.
Программирование и компьютерная графика также используют окружности. Множество алгоритмов, включая рисование окружностей, основаны на математических принципах, связанных с окружностями.
Круг, как особый вид окружности, имеет огромное применение. Он служит основой в повседневной жизни, начиная от блюд до колес на автомобилях. Кроме того, окружность используется в спорте, таком как футбол и баскетбол, где мячи имеют форму окружности.
Таким образом, окружность играет важную роль в разных областях нашей жизни, начиная от архитектуры и оптики до компьютерной графики и спорта. Понимание и умение работать с окружностью является необходимым для решения различных задач и производства объектов и устройств, которые мы используем ежедневно.