Равнобедренный треугольник привлекает внимание своей особенной формой, которая отличается от обычного треугольника. Это фигура, у которой две стороны равны и образуют угол у основания.
Определение основания равнобедренного треугольника играет важную роль при изучении его свойств и решении задач, связанных с этой геометрической фигурой. Основание равнобедренного треугольника - это сторона, которая не прилегает к вершине, образующей два равных угла. Таким образом, две другие стороны равнобедренного треугольника называются равными боковыми сторонами.
Определение основания равнобедренного треугольника помогает нам проще анализировать и решать задачи, связанные с данной геометрической фигурой. Известно, что у равнобедренного треугольника основание равностороннее, то есть внутренние углы, образованные основанием и равными боковыми сторонами, равны. Однако основание равнобедренного треугольника также может быть равносторонним, что означает, что основание и равные боковые стороны могут иметь одинаковую длину.
Основание равнобедренного треугольника
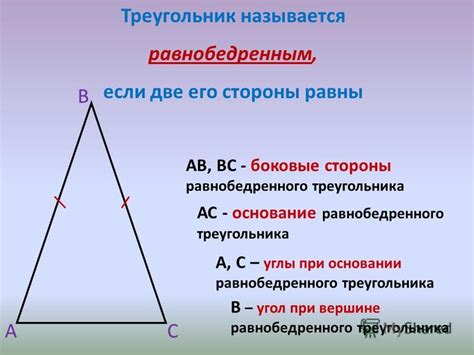
Определить основание равнобедренного треугольника можно с помощью его свойств. Для этого нужно знать длины всех сторон треугольника и углы, которые он образует. Если две стороны треугольника равны, то третья сторона будет основанием.
Основание равнобедренного треугольника играет важную роль в его геометрии. Оно определяет размеры и форму фигуры, а также связано с другими свойствами треугольника, такими как периметр и площадь. Знание основания позволяет проводить различные геометрические вычисления и решать задачи на их основе.
Основные понятия
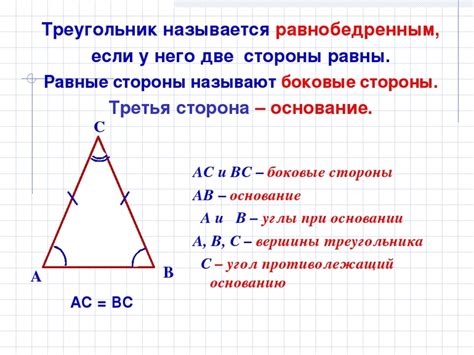
Треугольник является равнобедренным, если у него есть две равные стороны и соответствующие им два равных угла. Основание в равнобедренном треугольнике обычно считается самой длинной стороной и находится между двумя равными углами.
Определение основания равнобедренного треугольника очень важно, так как оно помогает в решении различных геометрических задач, например, нахождении площади треугольника или нахождении других сторон и углов.
Основание равнобедренного треугольника обозначается буквой "b" и может быть вычислено с использованием различных методов, включая формулу пифагорова или использование теоремы косинусов.
Зная основание и некоторые другие параметры равнобедренного треугольника, можно решить множество геометрических задач и получить дополнительные сведения о треугольнике.
Определение равнобедренного треугольника
Равнобедренным треугольником называется треугольник, у которого две стороны равны друг другу, а третья сторона отличается от них. Так как треугольник состоит из трех сторон, то равнобедренными треугольниками могут быть только те треугольники, у которых все три стороны равны друг другу. Такой треугольник имеет две равные углы при основании, которые называются основаниями равнобедренного треугольника.
| Основание | Основание |
|---|---|
| Сторона | Сторона |
Определить основание равнобедренного треугольника можно либо по длине его сторон, либо по длине его высоты, которая проведена из вершины треугольника к основанию. Если две стороны треугольника равны, то их острый угол при вершине также будет равен. Основаниями равнобедренного треугольника являются стороны, не равные друг другу, и сторона, отличная от них.
Определение сторон треугольника
В треугольнике существуют три стороны - AB, BC и CA, которые обычно обозначаются маленькими буквами a, b и c соответственно.
Сторона треугольника - это отрезок, соединяющий две его вершины. Прямая, на которой лежит сторона треугольника, называется стороной треугольника.
Длина стороны треугольника определяется как расстояние между двумя ее конечными точками. Для измерения длины сторон треугольника можно использовать линейку или другой инструмент измерения.
Важно отметить, что в равнобедренном треугольнике две стороны равны друг другу. Это значит, что длины сторон AB и AC равны, а сторона BC имеет отличную от них длину.
На основе длин сторон треугольника можно выполнять различные геометрические расчеты и конструкции, такие как вычисление площади треугольника, определение его высоты и нахождение углов треугольника.
В геометрии стороны треугольника играют важную роль, и их изучение помогает понять структуру и свойства треугольника, а также применять эти знания в решении геометрических задач.
Свойства основания

- Основание равнобедренного треугольника является самой длинной из его сторон.
- Длина основания влияет на высоту треугольника. Чем больше основание, тем меньше высота, и наоборот.
- Перпендикуляр, опущенный из вершины треугольника на его основание, делит основание пополам.
- Длина основания может быть использована для вычисления площади равнобедренного треугольника по формуле: площадь = (база * высота) / 2.
Эти свойства основания равнобедренного треугольника помогают лучше понять его геометрические характеристики и использовать их в решении задач и вычислениях.
Применение основания

Основание играет важную роль в вычислениях и применении равнобедренного треугольника. Во-первых, зная длину основания и значение угла между основанием и боковой стороной, можно определить длину других сторон треугольника. Это позволяет решать задачи по геометрии и тригонометрии с использованием равнобедренных треугольников.
Во-вторых, в некоторых случаях основание равнобедренного треугольника служит опорой или опорной линией. Например, в архитектуре основание равнобедренного треугольника может быть использовано для строительства фундамента здания или создания арки или пролета.
Также основание может использоваться для вычисления площади равнобедренного треугольника. Формула для вычисления площади треугольника использует длину основания и высоту, которая проведена из вершины треугольника к основанию. Площадь треугольника можно вычислить по формуле:
S = (a * h) / 2, где S - площадь треугольника, a - длина основания, h - высота треугольника.
Применение основания равнобедренного треугольника в различных областях знаний подтверждает его важность и универсальность.