Равнобедренный треугольник – это треугольник, у которого две стороны равны по длине. В свою очередь, основание равнобедренного треугольника – это та из двух равных сторон, на которой треугольник опирается. Но как найти длину основания, если мы знаем длину других сторон?
Существуют разные способы расчета основания равнобедренного треугольника. Один из самых простых и классических способов – использование формулы площади треугольника. Если мы знаем длину высоты треугольника, то можем найти площадь, а затем и длину основания. Для этого можем использовать формулу S = 0.5 * a * h, где a – длина основания, h – длина высоты.
Еще один способ нахождения основания равнобедренного треугольника – использование теоремы Пифагора. Мы знаем, что квадрат длины основания равен сумме квадратов половины основания и длины боковой стороны. Таким образом, если мы знаем длину боковой стороны и половину основания, можем найти длину основания, применив теорему Пифагора.
Определение равнобедренного треугольника
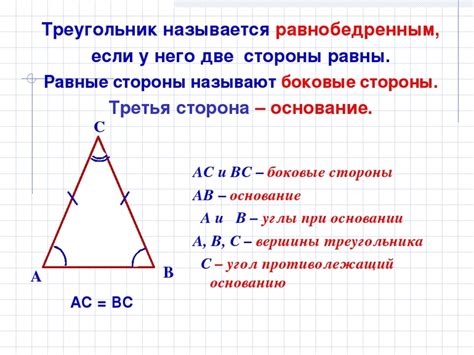
Определить равнобедренный треугольник можно по следующим признакам:
- У треугольника две равные стороны
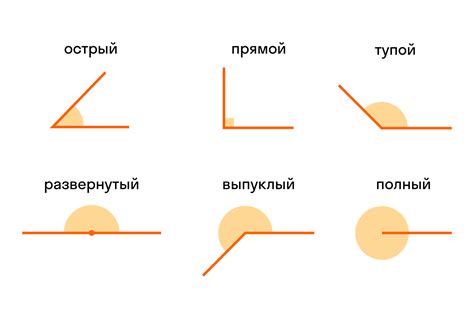
- У треугольника два равных угла, образованных равными сторонами
- У треугольника один угол равен 90 градусов
Равнобедренные треугольники имеют массу применений в геометрии и других науках. Они используются для решения различных задач, включая нахождение площади треугольника, вычисление высоты и медиан, а также проведение различных конструкций.
Геометрические свойства равнобедренного треугольника
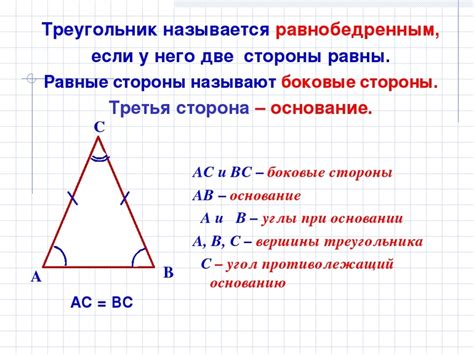
1. Углы равнобедренного треугольника
В равнобедренном треугольнике острый угол, образованный между равными сторонами, является наименьшим углом треугольника. Кроме того, вершина острого угла лежит на биссектрисе основания треугольника.
2. Биссектрисы равнобедренного треугольника
Биссектрисы углов равнобедренного треугольника равны и пересекаются в одной точке – центре вписанной окружности. Центр вписанной окружности равнобедренного треугольника совпадает с центром симметрии этого треугольника.
3. Высота равнобедренного треугольника
Высота равнобедренного треугольника, проведенная из вершины угла, образованного основанием и равными сторонами, является биссектрисой этого угла и медианой треугольника. При этом она делит треугольник на два равных прямоугольных треугольника, каждый из которых является подобным исходному треугольнику.
Знание этих геометрических свойств равнобедренного треугольника позволяет использовать их для нахождения различных значений и решения задач, связанных с этим типом треугольников.
Основание равнобедренного треугольника
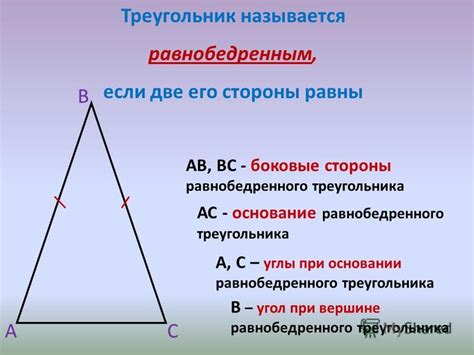
Для расчета длины основания равнобедренного треугольника с известными длинами его равных сторон необходимо использовать соответствующую формулу.
Если длина общей стороны равна a, а длина основания равна b, то по теореме Пифагора можно определить их связь:
b = 2 * sqrt(a² - (a/2)²) = 2 * sqrt(3 * a² / 4) = a * sqrt(3)
Таким образом, основание равнобедренного треугольника всегда равно длине равной стороны, умноженной на √3.
Зная длину равных сторон, можно легко расчитать длину основания этого треугольника, используя данную формулу.
Это свойство равнобедренных треугольников позволяет использовать их для решения различных задач в геометрии и математике.
Основание как биссектриса
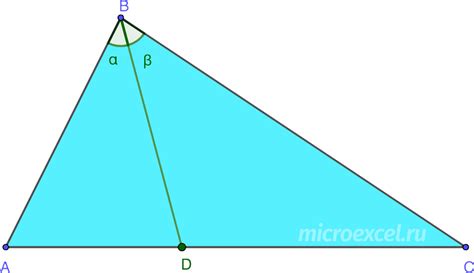
Биссектриса – это линия, которая делит угол на две равные части. В случае равнобедренного треугольника, биссектриса делит основание на две равные части, а также перпендикулярна ему.
Для расчета основания треугольника по биссектрисе используются следующие формулы:
- Найдите площадь треугольника по формуле: S = √(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника, a, b, c - длины сторон.
- Найдите высоту треугольника по формуле: h = 2 * S / основание.
- Найдите длину биссектрисы треугольника по формуле: биссектриса = 2 * S / (a + b + c).
- Найдите половину основания треугольника, которая будет равна половине длины биссектрисы.
После получения значения половины основания, умножьте его на 2, чтобы получить длину всего основания равнобедренного треугольника.
Используя этот метод расчета, можно определить длину основания, зная длины сторон и биссектрисы треугольника.
Основание как медиана

Для того чтобы найти основание треугольника, когда известны длины его сторон, можно воспользоваться формулой:
Основание = 2 * √(сторона^2 - (0.25 * диагональ^2))
Где сторона - длина боковой стороны треугольника, а диагональ - длина отрезка, соединяющего основание и вершину треугольника.
Используя эту формулу, можно легко вычислить длину основания равнобедренного треугольника, если известны длины его сторон и диагональ. Такой способ особенно удобен, когда нужно быстро и точно определить основание, не проводя дополнительные измерения.
Основание как высота
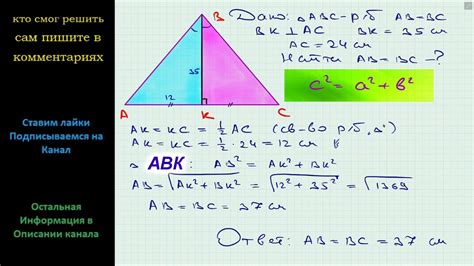
Для того чтобы найти длину основания, необходимо знать высоту треугольника и длину одного из двух равных боковых сторон. Высотой называется отрезок, проведенный из вершины треугольника до основания, перпендикулярный к основанию.
Формула для нахождения основания треугольника через его высоту имеет вид:
основание = 2 * (площадь треугольника) / (высота треугольника)
Зная высоту и площадь равнобедренного треугольника, можно легко найти его основание.
Таким образом, основание треугольника может быть найдено, если известна его высота и одна из сторон.
Преимущество использования основания как высоты заключается в том, что для ее определения достаточно знать только высоту и одну из сторон треугольника, что делает расчет более простым и быстрым.
Основание через углы и стороны
Основание равнобедренного треугольника можно рассчитать, используя известные значения углов и сторон. Для этого необходимо знать две стороны и угол между ними.
Если известны длины сторон a и b, а также угол α между ними, то можно найти длину основания c по следующей формуле:
c = 2 * b * sin(α)
Здесь sin(α) - синус угла α, который можно найти с помощью тригонометрических таблиц или калькулятора.
Таким образом, зная значения двух сторон и угла между ними, можно вычислить длину основания равнобедренного треугольника.
Способы расчета основания равнобедренного треугольника
Существует несколько способов расчета основания равнобедренного треугольника:
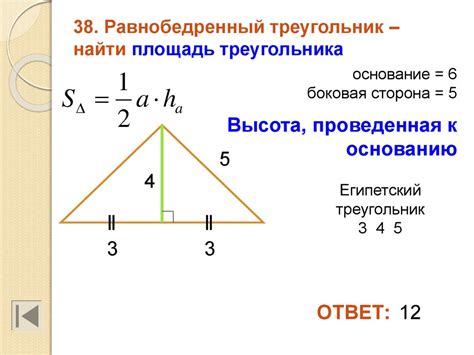
1. Использование теоремы Пифагора
Если известна длина боковой стороны и высота равнобедренного треугольника, то основание можно вычислить, применяя теорему Пифагора. Теорема Пифагора гласит, что квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов. Применяя эту теорему к половине основания и высоте, получаем уравнение для расчета основания: $(\frac{b}{2})^2 + h^2 = l^2$, где $b$ - основание, $h$ - высота, $l$ - боковая сторона. Решая это уравнение относительно $b$, мы можем получить значение основания.
2. Использование теоремы косинусов
Если известны длины двух сторон и угол между ними, то основание равнобедренного треугольника можно вычислить с помощью теоремы косинусов. Теорема косинусов гласит, что квадрат длины одной стороны треугольника равен сумме квадратов длин двух остальных сторон минус удвоенное произведение этих сторон на косинус угла между ними. Применяя эту теорему к основанию равнобедренного треугольника, получаем уравнение для расчета основания: $b^2 = l^2 - 2lh\cos(\frac{\alpha}{2})$, где $b$ - основание, $l$ - боковая сторона, $h$ - высота, $\alpha$ - угол между боковой стороной и основанием. Решая это уравнение относительно $b$, мы можем найти значение основания.
3. Использование формулы полупериметра
Если известны длины двух сторон и полупериметр треугольника, то основание равнобедренного треугольника можно вычислить с помощью формулы полупериметра. Полупериметр равен сумме длин всех сторон треугольника, разделенной на 2. Формула для расчета основания выглядит следующим образом: $b = 2p - l$, где $b$ - основание, $p$ - полупериметр, $l$ - боковая сторона. Решая это уравнение относительно $b$, мы можем получить значение основания.
Выбор способа расчета основания равнобедренного треугольника зависит от доступной информации о треугольнике. Для проведения точных вычислений рекомендуется использовать более сложные методы, такие как теорема Пифагора или теорема косинусов.