Окружности являются базовыми геометрическими фигурами, которые часто встречаются как в нашей повседневной жизни, так и в различных научных областях. При изучении окружностей одним из ключевых понятий является отношение радиусов пересекающихся окружностей.
Отношение радиусов пересекающихся окружностей может быть полезным при решении различных задач, например, при нахождении площади пересечения окружностей или при определении геометрических свойств фигур, которые образуются при пересечении окружностей.
Для нахождения отношения радиусов пересекающихся окружностей необходимо знать несколько ключевых понятий. Во-первых, стоит отметить, что отношение радиусов пересекающихся окружностей зависит от их взаимного расположения: окружности могут быть внешне касающимися, внутренне касающимися или пересекаться.
Отношение радиусов пересекающихся окружностей: основные понятия и определения

Радиус окружности – это отрезок, соединяющий центр окружности с любой ее точкой. Отношение радиусов двух пересекающихся окружностей могут быть различными в зависимости от размещения их центров и величины самих радиусов.
Основные определения, связанные с отношением радиусов пересекающихся окружностей, включают:
- Внешнее касание. Если окружности касаются друг друга только снаружи, их радиусы образуют отношение, равное отношению их радиусов.
- Внутреннее касание. Если окружности касаются друг друга только изнутри, отношение радиусов образует отношение, равное отношению их радиусов.
- Перекрывающиеся окружности. Если окружности пересекаются внутри и снаружи, отношение радиусов образует отношение, не равное отношению их радиусов.
Важно помнить, что для вычисления отношения радиусов пересекающихся окружностей необходимо знать значения их радиусов и положение их центров относительно друг друга.
Что такое радиус окружности и как он определяется?
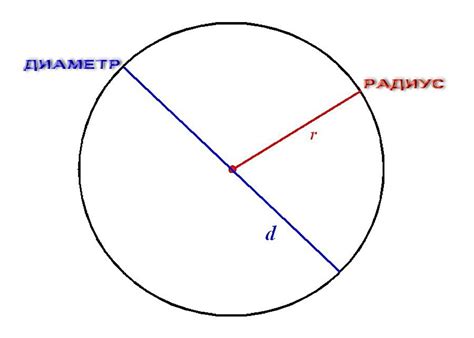
Радиус определяется по формуле: R = d/2, где "d" – диаметр окружности или отрезок, соединяющий любые две её точки через центр. Радиус также можно вычислить, зная площадь окружности по формуле S = πR^2, где π – это число "пи", приближенное значение которого равно 3,14159.
Радиус является характеристикой окружности, от которой зависят многие её свойства. Например, длина окружности вычисляется по формуле L = 2πR, где "L" – длина окружности. Также радиус определяет площадь окружности по формуле S = πR^2, где "S" – площадь.
Радиус окружности связывает её точки и центр, а также определяет размеры и форму данной геометрической фигуры. Знание радиуса позволяет рассчитывать различные параметры окружности и использовать эти знания в решении геометрических задач.
Как определить отношение радиусов пересекающихся окружностей?

Отношение радиусов пересекающихся окружностей можно определить, используя теорему о касательной, проведенной к окружности из точки пересечения двух окружностей.
Для этого необходимо провести линию, соединяющую центры пересекающихся окружностей, и определить точку их пересечения. Затем, из этой точки провести касательные к каждой из окружностей. Касательная будет пересекать окружность в точке касания.
Далее, можно определить отношение радиусов окружностей, используя два прямоугольных треугольника, образованных центром, точкой пересечения и точками касания с окружностями. Используя теорему Пифагора, отношение радиусов можно выразить как:
| О круги | Радиусы | Треугольник | Коэффициент |
|---|---|---|---|
| Первый | r1 | 1 | k = √r2 / √r1 |
| Второй | r2 | k = √r1 / √r2 |
Таким образом, отношение радиусов пересекающихся окружностей можно определить путем вычисления квадратного корня отношения радиусов каждой окружности.
Как связаны радиусы окружностей с их длинами?
Радиусы окружностей очень важны при изучении их свойств и взаимосвязей. Рассмотрим, как радиусы окружностей связаны с их длинами.
Длина окружности вычисляется по формуле:
L = 2πr ,
где L - длина окружности, а r - радиус.
| Радиус первой окружности | Радиус второй окружности | Разница радиусов (d) | Отношение длин окружностей |
|---|---|---|---|
| r1 | r2 | d = r1 - r2 | L1 / L2 = (r1 + d) / r2 |
Таким образом, отношение длин окружностей будет зависеть от разницы радиусов. Если разница радиусов положительна, то длина первой окружности будет больше длины второй. Если разница радиусов отрицательна, то длина второй окружности будет больше длины первой. В случае, если разница радиусов равна нулю, длины обеих окружностей будут одинаковыми.
Примеры задач на нахождение отношения радиусов пересекающихся окружностей

Ниже представлены несколько примеров задач, в которых необходимо найти отношение радиусов пересекающихся окружностей:
- Задача 1: Даны две окружности, радиус первой окружности равен 3 см, а радиус второй окружности равен 6 см. Найти отношение радиусов этих окружностей.
- Задача 2: В равнобедренном треугольнике ABC биссектриса угла A пересекает сторону BC в точке D. Центры описанной и вписанной окружностей этого треугольника обозначим соответственно O и I. Найдите отношение радиусов этих окружностей.
- Задача 3: Две окружности пересекаются в двух точках. Радиус первой окружности равен 5, а радиус второй окружности равен 8. Найти отношение радиусов этих окружностей.
Во всех этих задачах для нахождения отношения радиусов пересекающихся окружностей необходимо поделить радиус первой окружности на радиус второй окружности.
Практическое применение нахождения отношения радиусов пересекающихся окружностей

Нахождение отношения радиусов пересекающихся окружностей находит широкое применение в различных областях. Вот некоторые из них:
- Геометрия и теория чисел: Отношение радиусов пересекающихся окружностей может быть использовано для доказательства теорем и решения геометрических задач. Также, при изучении различных систем координат, знание отношения радиусов окружностей помогает понять связь между различными геометрическими фигурами.
- Физика: В физике отношение радиусов пересекающихся окружностей может быть использовано в различных расчетах. Например, при изучении движения твердых тел, знание отношения радиусов окружностей позволяет определить угловую скорость и момент инерции.
- Техника и строительство: В инженерных расчетах нахождение отношения радиусов пересекающихся окружностей может использоваться при проектировании и изготовлении различных механизмов и конструкций. Например, при проектировании колеса автомобиля необходимо учесть отношение радиусов, чтобы обеспечить правильную работу тормозной системы и подвески.
- Архитектура: В архитектуре отношение радиусов пересекающихся окружностей может быть использовано при проектировании круглых зданий, куполов и арок. Знание отношения радиусов позволяет определить строительные размеры и пропорции конструкции.
- Медицина: В медицине нахождение отношения радиусов пересекающихся окружностей может быть использовано при измерении размеров органов человека на рентгеновских снимках или при проведении ультразвукового исследования. Знание отношения радиусов позволяет определить объемы, площади и другие характеристики органов.
В целом, нахождение отношения радиусов пересекающихся окружностей является важным инструментом в различных областях и помогает решать разнообразные задачи. Надлежащее применение этого знания способно упростить и улучшить процессы проектирования, расчетов и анализа различных систем и конструкций.