Понимание пересечения и принадлежности прямой плоскости - важные аспекты геометрии, которые применяются в решении множества задач и проблем. Знание методов определения и правил, связанных с этими понятиями, помогает в анализе геометрических объектов и нахождении их характеристик.
Пересечение прямой и плоскости возникает, когда линия, заданная прямыми или кривыми, проходит через плоскость. Это может быть как обычное пересечение двух прямых на плоскости, так и пересечение прямой и плоскости в трехмерном пространстве. Для определения пересечения прямой и плоскости существуют различные методы, включая аналитический и графический подходы.
Принадлежность прямой плоскости определяет, лежит ли прямая на данной плоскости или нет. Для определения принадлежности необходимо проверить выполнение соответствующего уравнения, которое задает исходную прямую и плоскость. Существуют различные правила, позволяющие найти принадлежность прямой плоскости, включая проверку коэффициентов уравнения и использование точек, лежащих на прямой и плоскости.
Пересечение прямой и плоскости: основные понятия и методы
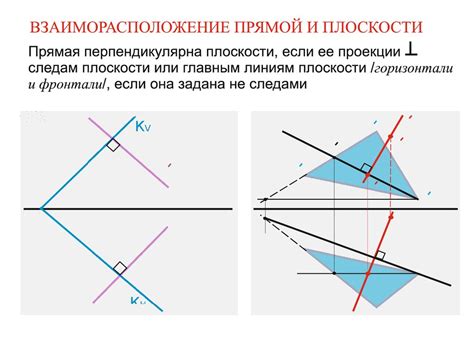
Пересечение прямой и плоскости возникает, когда прямая лежит в одной плоскости или пересекает ее в точке. Основными понятиями, используемыми при решении задач по пересечению прямой и плоскости, являются координаты точек, уравнение прямой и уравнение плоскости.
Методы определения пересечения прямой и плоскости включают:
- Метод подстановки, основанный на замене переменных в уравнении плоскости.
- Метод графического представления, позволяющий визуализировать прямую и плоскость на графике и определить их пересечение.
- Метод решения системы уравнений, при котором уравнения прямой и плоскости решаются одновременно, и находятся значения переменных, соответствующие точке пересечения.
Правила определения принадлежности прямой плоскости позволяют проверить, лежит ли заданная точка на прямой или в плоскости. Для этого обычно используются уравнения прямой и плоскости, и подставляются значения координат точки в эти уравнения.
Определение плоскости
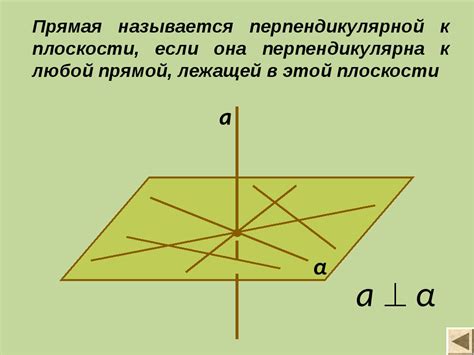
Существует несколько способов определения плоскости. Один из наиболее распространенных методов - указать три не коллинеарных точки, через которые проходит плоскость. Коллинеарными называются точки, лежащие на одной прямой. Таким образом, если есть три точки, которые не лежат на одной прямой, то их можно использовать для определения плоскости.
Если известны координаты трех не коллинеарных точек A(x₁, y₁, z₁), B(x₂, y₂, z₂) и C(x₃, y₃, z₃), то плоскость, проходящая через эти точки, может быть задана уравнением:
- Ax + By + Cz + D = 0
где A, B, C и D - коэффициенты, которые можно найти, используя известные координаты точек.
Другой способ определения плоскости - использовать векторы. Если известно, что плоскость проходит через некоторую точку A(x₀, y₀, z₀) и параллельна заданным векторам v₁(x₁, y₁, z₁) и v₂(x₂, y₂, z₂), то плоскость может быть описана уравнением:
- (x - x₀, y - y₀, z - z₀) ⋅ n = 0
где x, y и z - координаты любой точки на плоскости, (x - x₀, y - y₀, z - z₀) - вектор, соединяющий точку на плоскости с точкой A, ⋅ обозначает скалярное произведение, а n - нормальный вектор плоскости, который можно найти как векторное произведение заданных векторов v₁ и v₂.
Определение прямой
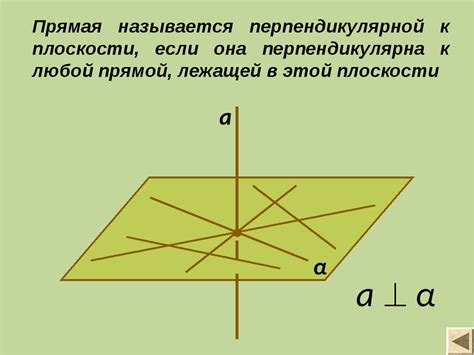
В геометрии прямые обычно обозначаются буквами латинского алфавита, например, AB или CD. Для того чтобы однозначно определить прямую, необходимо указать две ее точки или же одну точку и ее направление.
Прямая может быть определена с использованием уравнений. Наиболее общим уравнением прямой на плоскости является уравнение вида y = kx + b, где k – это коэффициент наклона прямой, а b – свободный член. Уравнение прямой в трехмерном пространстве может быть представлено в виде системы уравнений, например, x = a + bt, y = c + dt и z = e + ft, где a, b, c, d, e, f – коэффициенты прямой и t – параметр.
Важно отметить, что прямые также могут быть заданы векторными уравнениями или геометрическими условиями (например, совпадение с другой прямой или плоскостью).
| Примеры уравнений прямых на плоскости | Примеры уравнений прямых в пространстве |
|---|---|
| y = 2x + 3 | x = 1 + t, y = 2 + 2t, z = 3 + 3t |
| y = -5x + 2 | x = 2 + t, y = 1 + 3t, z = 4 + 4t |
Определение прямой позволяет решать множество геометрических задач, таких как нахождение пересечений с другими прямыми или плоскостями, определение расстояний и углов, построение графиков и многое другое.
Как определить пересечение прямой и плоскости

Существует несколько методов и правил, которые помогают определить пересечение прямой и плоскости.
Один из способов – использование уравнения плоскости и уравнения прямой. Если подставить координаты точки прямой в уравнение плоскости и получить верное равенство, значит, прямая пересекает плоскость. Если равенство не выполняется, то прямая и плоскость не пересекаются.
Ещё один метод – построение перпендикуляров. Если один из перпендикуляров, взятых из любой точки прямой, проведённых к плоскости, пересекает её, значит, прямая и плоскость пересекаются. Если все перпендикуляры не пересекают плоскость, значит, прямая и плоскость не имеют точек пересечения.
Также можно использовать коэффициенты уравнений плоскости и прямой для определения пересечения. Если эти коэффициенты не равны нулю и не равны друг другу, значит, прямая и плоскость пересекаются. Если хотя бы один из коэффициентов равен нулю, а другой не равен нулю, пересечения нет.
| Метод | Условие пересечения | Отсутствие пересечения |
|---|---|---|
| Подстановка точки прямой в уравнение плоскости | Уравнение верное | Уравнение не выполняется |
| Построение перпендикуляров | Перпендикуляр пересекает плоскость | Перпендикуляр не пересекает плоскость |
| Коэффициенты уравнений | Коэффициенты не равны нулю и друг другу | Коэффициенты равны нулю или равны друг другу |
Важно помнить, что при определении пересечения прямой и плоскости необходимо учитывать точность вычислений и особенности конкретных задач. Использование различных методов и правил может быть полезно для подтверждения или опровержения пересечения между прямой и плоскостью.
Методы определения пересечения
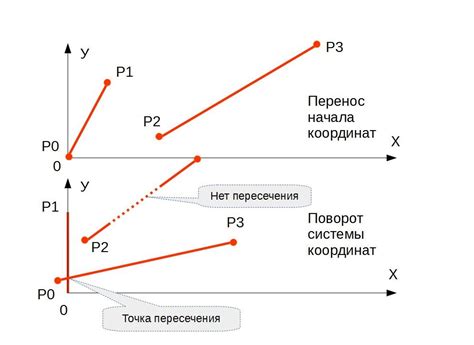
Первый метод - аналитический. С его помощью можно определить уравнение прямой и плоскости и затем найти их точки пересечения. Для этого используются различные формы уравнений, такие как общее уравнение прямой и уравнение плоскости.
Второй метод - графический. С помощью этого метода можно визуализировать прямую и плоскость на графике и определить их пересечение. Для этого строится график прямой и просматривается, пересекает ли она плоскость.
Третий метод - векторный. Он основан на использовании векторов для определения пересечения прямой и плоскости. С помощью векторных операций можно найти точку пересечения или определить принадлежность точки прямой или плоскости.
Независимо от выбранного метода, важно правильно использовать его для определения пересечения прямой и плоскости. Кроме того, следует учитывать особенности конкретных прямых и плоскостей, такие как их положение и ориентация в пространстве.
| Метод | Принцип | Применение |
|---|---|---|
| Аналитический | Использование уравнений прямой и плоскости | Точное определение пересечения |
| Графический | Визуализация прямой и плоскости на графике | Относительное определение пересечения |
| Векторный | Использование векторных операций | Комплексное определение пересечения |
Выбор метода определения пересечения прямой и плоскости зависит от конкретной ситуации и требуемой точности результатов. Важно учитывать особенности задачи и выбрать наиболее подходящий метод для ее решения.
Правила определения принадлежности прямой к плоскости
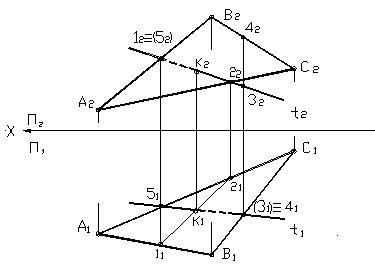
- Если прямая лежит внутри плоскости и не пересекает ее, то она принадлежит этой плоскости. В этом случае говорят, что прямая и плоскость совпадают.
- Если прямая пересекает плоскость в одной точке, то она принадлежит этой плоскости.
- Если прямая пересекает плоскость в двух различных точках, то она не принадлежит этой плоскости. В этом случае говорят, что прямая и плоскость пересекаются.
- Если прямая пересекает плоскость только в одной точке и лежит вне этой плоскости, то она не принадлежит этой плоскости. В этом случае говорят, что прямая и плоскость не пересекаются.
Для определения принадлежности прямой к плоскости также можно использовать уравнение прямой и уравнение плоскости. Если координаты точки, через которую проходит прямая, удовлетворяют уравнению плоскости, то прямая принадлежит этой плоскости.
Определение принадлежности прямой к плоскости имеет важное значение не только в математике, но и в других областях. Например, в компьютерной графике и инженерии такие понятия, как пересечение прямой с плоскостью и принадлежность прямой к плоскости, используются для построения трехмерных моделей и расчетов конструкций.
Важные моменты при определении пересечения и принадлежности
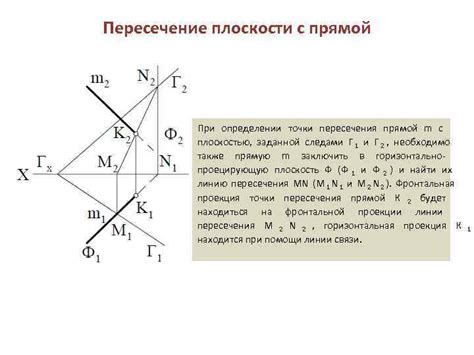
1. Уравнение прямой и плоскости: перед определением пересечения и принадлежности, необходимо иметь уравнения прямой и плоскости. Уравнение прямой обычно задается в виде Ах + By + C = 0, где A, B и C - коэффициенты, а x и y - переменные. Уравнение плоскости задается в виде Aх + By + Cz + D = 0, где A, B, C и D - коэффициенты, а x, y и z - переменные.
2. Пересечение: для определения пересечения прямой и плоскости, подставьте координаты точки прямой в уравнение плоскости. Если полученное равенство выполняется, то прямая пересекает плоскость. Если же равенство не выполняется, то прямая и плоскость не пересекаются.
3. Принадлежность: для определения принадлежности точки плоскости, подставьте координаты этой точки в уравнение плоскости. Если полученное равенство выполняется, то точка принадлежит плоскости. Если равенство не выполняется, значит точка не принадлежит плоскости.
Учет этих важных моментов позволяет корректно определить пересечение и принадлежность прямой и плоскости. Знание уравнений прямой и плоскости, а также применение их в формулах, помогает решать различные геометрические задачи и находить нужные ответы.
Применение методов в задачах геометрии

Один из основных методов - это использование уравнений прямой и плоскости. Через уравнения можно определить точку пересечения прямой с плоскостью и проверить принадлежность данной точки к плоскости.
Также можно использовать метод векторов, определяя векторы, соответствующие прямой и плоскости, и проверяя их перпендикулярность или коллинеарность. Если вектор прямой перпендикулярен вектору плоскости, то прямая пересекает плоскость в одной точке. Если векторы коллинеарны, то прямая лежит в данной плоскости.
Другой метод - это использование координат точек. Зная координаты точек, принадлежащих прямой и плоскости, можно проверять их взаимное расположение. Если координаты точки принадлежности прямой лежат в уравнении плоскости, то прямая пересекает плоскость. Если координаты точки принадлежности прямой лежат на прямой, то прямая принадлежит плоскости.
Эти методы находят применение в различных задачах геометрии, таких как построение трехмерных моделей, определение пересечений линий и плоскостей, нахождение точек отражения и прочее. Они являются надежными инструментами для решения геометрических задач и позволяют получить точные и надежные результаты.