Треугольник – это одна из базовых геометрических фигур, которая имеет три стороны и три угла. Он часто встречается в различных задачах, связанных с геометрией и физикой. Когда мы знаем высоту и площадь треугольника, нам может понадобиться найти его периметр. В этой статье мы рассмотрим, как это сделать.
Периметр – это сумма длин всех сторон треугольника. Он играет важную роль в решении многих задач, связанных с геометрией. Таким образом, зная высоту и площадь треугольника, можно найти его периметр с помощью определенных формул.
Существует несколько способов найти периметр треугольника по высоте и площади. Один из самых простых – это воспользоваться формулой, которая связывает площадь треугольника с его высотой. Для этого нам понадобится знать одну из сторон треугольника. Если известна площадь (S) и высота (h) треугольника, а также известна одна из его сторон (a), то можно найти периметр (P) с помощью следующей формулы: P = a + a + (2*S/a)
Как найти периметр треугольника
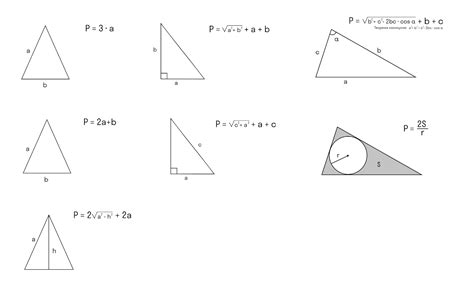
Периметр треугольника вычисляется как сумма длин его сторон. Существует несколько способов нахождения периметра треугольника, в зависимости от известных данных.
1. Если известны длины всех трех сторон треугольника, то периметр можно найти, сложив эти значения:
- Сторона А: a
- Сторона B: b
- Сторона C: c
Периметр треугольника равен сумме a, b и c: P = a + b + c.
2. Если известна высота треугольника и длины двух его сторон, то периметр можно найти, используя известные данные и теорему Пифагора:
- Основание треугольника: a
- Высота треугольника, опущенная на основание: h
- Боковая сторона треугольника: b
Периметр треугольника можно найти по формуле: P = a + b + 2 * (h^2 + b^2)^(1/2).
3. Если известны площадь треугольника и длины двух его сторон, можно использовать известные данные и формулу для нахождения высоты треугольника:
- Основание треугольника: a
- Боковая сторона треугольника: b
- Площадь треугольника: S
Высоту треугольника можно найти по формуле: h = 2 * S / a. После нахождения высоты, периметр треугольника можно найти, используя известные данные из пункта 2.
Найденный таким образом периметр треугольника может быть использован для решения различных задач, связанных с этой фигурой.
Высота и площадь треугольника
Высота треугольника - это перпендикуляр, опущенный из вершины треугольника на противоположную сторону. Величина высоты обозначается как h.
Площадь треугольника можно найти, зная его высоту (h) и длины основания (b). Формула для расчета площади следующая:
S = (b * h) / 2
Где S - площадь треугольника, b - длина основания, h - высота треугольника.
Расчет площади треугольника по известным значениям высоты и основания особенно полезен, когда измерить стороны треугольника затруднительно.
Зная площадь треугольника и одну из его сторон (a), можно найти величину высоты, используя следующую формулу:
h = (2 * S) / a
Применение этих формул позволяет находить высоту и площадь треугольника, что может быть полезно при решении геометрических задач и на практике в других областях.
Обратите внимание, что величина высоты и площади треугольника зависит от выбранной основы (стороны треугольника).
Математические формулы для расчета
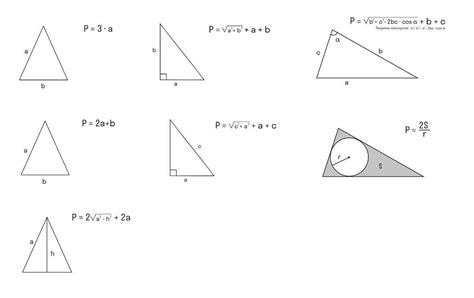
Для расчета периметра треугольника по высоте и площади можно использовать следующие математические формулы:
- Формула для вычисления основания треугольника:
- Формула для расчета периметра треугольника:
b = \frac{2 \cdot S}{h}
где b - основание треугольника, S - площадь треугольника, h - высота треугольника.
P = 2 \cdot c + b
где P - периметр треугольника, c - сторона треугольника, b - основание треугольника.
Используя эти формулы, вы сможете легко и точно найти периметр треугольника по заданной высоте и площади. Это может быть полезно при решении различных задач и заданий по геометрии.
Примеры расчетов периметра треугольника
Рассмотрим несколько примеров расчета периметра треугольника по заданной высоте и площади.
Пример 1:
Дано: высота треугольника - 6 см, площадь треугольника - 12 кв. см.
Решение: сначала найдем длину основания треугольника, используя формулу площади:
Площадь = (основание * высота) / 2
12 = (основание * 6) / 2
Основание = 4 см
Теперь можем найти периметр треугольника, используя найденное основание и высоту:
Периметр = основание + 2 * боковая сторона
Периметр = 4 + 2 * боковая сторона
Для расчета боковой стороны воспользуемся теоремой Пифагора:
боковая сторона = корень из (основание^2 + высота^2)
боковая сторона = корень из (4^2 + 6^2)
боковая сторона = корень из (16 + 36)
боковая сторона = корень из 52
боковая сторона ≈ 7.211
Периметр ≈ 4 + 2 * 7.211
Ответ: периметр треугольника ≈ 18.422 см.
Пример 2:
Дано: высота треугольника - 8 см, площадь треугольника - 20 кв. см.
Решение: аналогично первому примеру, найдем длину основания треугольника:
Площадь = (основание * высота) / 2
20 = (основание * 8) / 2
Основание = 10 см
Теперь можем найти периметр треугольника, используя найденное основание и высоту:
Периметр = основание + 2 * боковая сторона
Периметр = 10 + 2 * боковая сторона
Расчет боковой стороны:
боковая сторона = корень из (основание^2 + высота^2)
боковая сторона = корень из (10^2 + 8^2)
боковая сторона = корень из (100 + 64)
боковая сторона = корень из 164
боковая сторона ≈ 12.806
Периметр ≈ 10 + 2 * 12.806
Ответ: периметр треугольника ≈ 35.612 см.
В данных примерах мы использовали формулы поиска периметра и площади треугольника, а также теорему Пифагора для нахождения боковой стороны. Учитывайте эти методы, чтобы проводить расчеты и в других задачах.