Тригонометрические функции – это функции, которые связаны с углами, и широко используются в различных областях науки и техники. Одним из важных понятий, связанных с тригонометрическими функциями, является периодичность.
Периодичность – это свойство функции, при котором её значения повторяются через равные промежутки времени или пространства. В контексте тригонометрических функций период указывает на наименьший угол, при котором значение функции повторяется. Например, функции синуса и косинуса являются периодическими с периодом 2π.
Определить периодичность тригонометрической функции можно с помощью различных методов. Наиболее распространенным способом является анализ числовых значений функции на интервале, достаточном для определения периода. Для этого можно вычислить значения функции в нескольких точках на заданном интервале и затем проанализировать полученные результаты.
Определение периодичности

Периодичность тригонометрической функции означает, что функция повторяется с определенным интервалом. Для определения периода функции можно использовать несколько методов:
1. Графический метод:
Графический метод заключается в построении графика функции и определении интервалов, на которых функция повторяет свое значение. Если функция повторяется через равные интервалы, то период функции будет равен этому интервалу.
Пример:
Построим график функции y = sin(x) и обнаружим, что функция повторяется каждые 2π единицы по оси x. То есть, период функции равен 2π.
2. Аналитический метод:
Аналитический метод основан на анализе алгебраического выражения функции. Для тригонометрических функций, период можно найти по следующей формуле:
T = 2π/ω
где Т - период функции, а ω - частота колебаний функции.
Например, для функции y = cos(2x), период будет равен 2π/2 = π.
Используя графический и аналитический методы, можно точно определить периодичность тригонометрической функции и использовать эту информацию для решения задач и построения графиков.
Что такое периодичность тригонометрической функции
В геометрическом смысле периодичность функции означает, что график функции повторяется вдоль оси абсцисс через определенное расстояние.
Для тригонометрических функций таких как синус, косинус и тангенс, периодичность определяется через значение угла.
- Период синуса и косинуса равен 2π (или 360°).
- Период тангенса равен π (или 180°).
То есть, если мы измеряем значения функций синуса, косинуса или тангенса при каждом кратном периоде, мы получим одинаковый результат. Например, sin(0) = sin(2π) = sin(4π) и т.д.
Имея информацию о периоде тригонометрической функции, можно использовать это свойство для решения уравнений, нахождения значений функции, а также для построения графиков функций и анализа их поведения.
Параметры определения периодичности

Вторым параметром является коэффициент, который умножается на аргумент. Коэффициент влияет на масштабирование графика функции и может влиять на ее периодичность. Если коэффициент равен 1, то периодичность функции сохраняется. Если коэффициент больше 1, то график функции "растягивается" вдоль оси x. Если коэффициент меньше 1, то график функции "сжимается".
Третьим параметром является фазовый сдвиг функции. Фазовый сдвиг определяет, насколько график функции сдвигается вдоль оси x относительно начала координат. Фазовый сдвиг может быть положительным или отрицательным числом.
Итак, для определения периодичности тригонометрической функции необходимо учитывать аргумент, коэффициент и фазовый сдвиг. Точное определение периодичности требует рассмотрения каждого параметра и разбора функции в целом.
Определение периода функции

Определить период функции можно, зная ее график или аналитическое выражение. Если функция задана графически, необходимо найти расстояние между двумя соседними максимумами или минимумами функции на графике. Это расстояние и будет являться периодом функции.
Если функция задана аналитически, можно использовать следующий алгоритм:
| Шаг | Действие |
|---|---|
| 1 | Решите уравнение f(x) = f(x + T), где T - возможное значение периода функции. |
| 2 | Найдите все значения T, которые удовлетворяют уравнению. |
| 3 | Выберите наименьшее положительное значение T из найденных. Это и будет периодом функции. |
Например, для функции синуса, уравнение f(x) = f(x + 2π) решается следующим образом:
sin(x) = sin(x + 2π)
sin(0) = sin(2π)
0 = 0
Таким образом, период функции синус равен 2π.
Зная период функции, можно определить повторяемость значений функции на всей числовой прямой и строить ее график.
Понятие периода в математике

Для тригонометрических функций период определяется как наименьшая положительная константа, при которой функция повторяет свои значения. Наиболее известными тригонометрическими функциями, обладающими периодами, являются синус, косинус и тангенс.
Период синуса и косинуса – это 2π. Это означает, что эти функции повторяют свои значения каждые 2π радиан.
Например, синус угла 0° равен 0, а синус угла 360° также равен 0. Таким образом, синус функции повторяет свои значения каждые 360° или 2π радиан.
Тангенс, секанс, котангенс и косеканс имеют период π. Это означает, что эти функции повторяют свои значения каждые π радиан или 180°.
Периодические функции встречаются не только в тригонометрии, но и в других разделах математики и естественных науках. Изучение периодов функций позволяет предсказать и анализировать поведение этих функций на определенных промежутках.
Определение периода тригонометрической функции является важным шагом при анализе и решении уравнений, графическом представлении функций и многих других математических операциях. Поэтому понимание периода является необходимым для различных областей науки и инженерии.
| Тригонометрическая функция | Период |
|---|---|
| Синус | 2π |
| Косинус | 2π |
| Тангенс | π |
| Секанс | π |
| Котангенс | π |
| Косеканс | π |
Узнавание периода тригонометрической функции
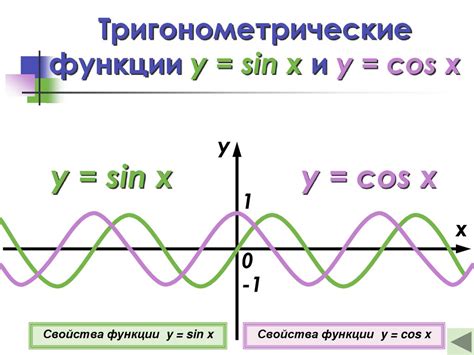
Для определения периода тригонометрической функции необходимо учесть, какие изменения происходят в функции при изменении аргумента. Наиболее часто используемыми тригонометрическими функциями являются синус и косинус, поэтому рассмотрим определение периода для этих функций.
Для синуса и косинуса период равен 2π, что означает, что эти функции повторяются снова и снова через каждые 2π радиан. Из этого следует, что значения функций синуса и косинуса находятся в точности на тех же позициях в своих периодах и выполняют одинаковые изменения. Например, синус и косинус имеют значение 0 в точке 0, их значения равны 1 и -1 в точках π/2 и 3π/2 соответственно.
Таким образом, зная период тригонометрической функции, можно с легкостью вычислить ее значения в любой точке, а также предсказать изменения в функции на протяжении всего периода. Это делает период очень важным понятием в изучении тригонометрических функций и их применении в различных областях науки и техники.