Одним из важных аспектов анализа функций является определение периодов их возрастания и убывания. Это позволяет нам лучше понять, как функция меняется на определенных участках своей области определения. В этой статье мы рассмотрим несколько полезных советов и примеров для нахождения этих периодов.
Периоды возрастания функции определяются теми участками, на которых она строго возрастает. Иными словами, это участки, на которых значения функции увеличиваются по мере изменения аргумента. Чтобы найти эти периоды, нужно проанализировать производную функции. Если производная положительна на каком-то интервале, то функция возрастает на этом интервале.
Периоды убывания функции, наоборот, определяются участками, на которых она строго убывает. То есть, значения функции уменьшаются по мере изменения аргумента. Для поиска этих периодов также нужно проанализировать производную функции. Если производная отрицательна на каком-то интервале, то функция убывает на этом интервале.
Например, рассмотрим функцию f(x) = x2. Ее производная равна f'(x) = 2x. Чтобы определить периоды возрастания и убывания функции, нужно решить уравнения f'(x) > 0 и f'(x) < 0 соответственно. В данном случае, область возрастания функции будет (-∞, 0) U (0, +∞), а область убывания - пустое множество.
Итак, зная некоторые основные принципы анализа функций и умея находить периоды возрастания и убывания, мы можем более полно и точно описывать их поведение. Это позволяет нам лучше понимать, как они функционируют и использовать это знание в различных задачах и приложениях.
Определение периодов возрастания и убывания функции
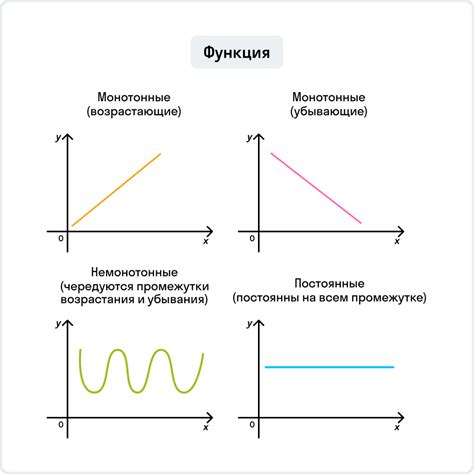
Для определения периода возрастания функции необходимо найти интервалы, на которых производная положительна. На таких интервалах функция будет строго возрастать. То есть, если производная больше нуля, то функция возрастает.
Аналогично, для определения периода убывания функции нужно найти интервалы, на которых производная отрицательна. На таких интервалах функция будет строго убывать. То есть, если производная меньше нуля, то функция убывает.
Для нахождения периодов возрастания и убывания функции следует выполнить следующие шаги:
- Вычислить производную функции.
- Решить неравенство производной относительно нуля.
- Найти интервалы, на которых производная меньше или больше нуля.
- Объединить найденные интервалы и откройте скобку, если функция убывает или закройте скобку, если функция возрастает.
Например, рассмотрим функцию f(x) = x^2 - 1. Производная этой функции равна f'(x) = 2x. Чтобы найти периоды возрастания и убывания, решим неравенство 2x > 0. Отсюда получаем, что x > 0. Таким образом, функция возрастает на интервале (0, +∞).
Таким образом, определение периодов возрастания и убывания функции является важным шагом при анализе ее поведения и может помочь в решении различных задач в математике и других областях.
Значение производной и ее роль в поиске периодов
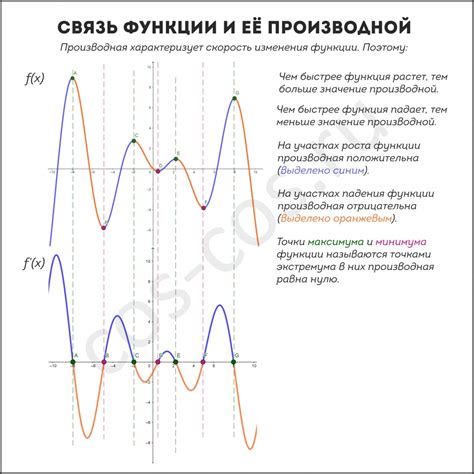
Если производная функции положительна в каком-то интервале, то функция возрастает на этом интервале. Это означает, что значения функции в этом интервале увеличиваются с увеличением аргумента. Таким образом, период возрастания функции можно определить, исследуя значения производной в разных точках.
В случае, когда производная функции отрицательна в каком-то интервале, функция убывает на этом интервале. Это означает, что значения функции в этом интервале уменьшаются с увеличением аргумента. Путем анализа значений производной в разных точках можно определить периоды убывания функции.
Чтобы найти периоды возрастания и убывания функции, необходимо найти значения производной функции и проанализировать их знаки. Знаки производной помогают определить, когда функция возрастает или убывает, а точки, в которых производная равна нулю, являются границами этих периодов.
Используя методы дифференциального исчисления, можно вычислить производную функции и построить ее график. На этом графике можно определить периоды возрастания и убывания функции и провести дальнейший анализ функции.
Итак, значение производной функции и ее знаки играют важную роль в поиске периодов возрастания и убывания функции. Анализ производной позволяет определить, как меняется функция в разных точках и найти периоды изменения ее значений.
Алгоритм поиска периода возрастания функции
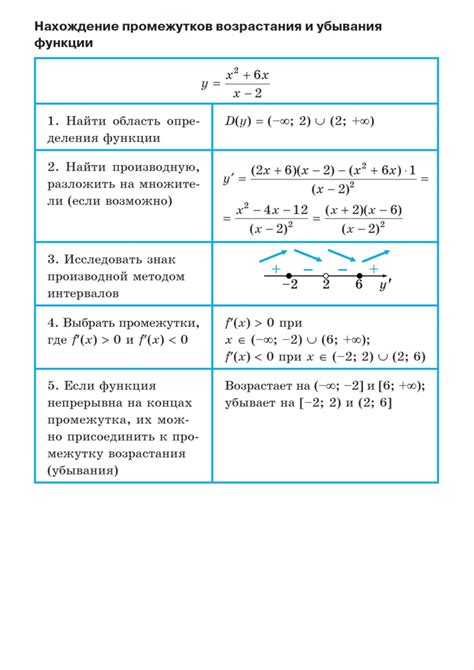
Для нахождения периодов возрастания функции необходимо выполнить следующие шаги:
- Найдите все точки, в которых производная функции равна нулю или не определена. Эти точки могут являться границами периодов возрастания или убывания функции.
- Разделите область определения функции на интервалы между найденными точками.
- Выберите произвольную точку из каждого интервала и подставьте их значения в производную функции.
- Определите знак производной в каждой выбранной точке. Если производная положительна, то функция возрастает на соответствующем интервале. Если производная отрицательна, то функция убывает на интервале.
- Выполните проверку, чтобы удостовериться в правильности найденных интервалов. Для этого подставьте значения выбранных точек в исходную функцию и убедитесь, что на интервалах она действительно возрастает или убывает.
При правильном выполнении указанных шагов, вы сможете точно определить периоды возрастания функции и использовать эту информацию для анализа и построения графиков.
Пример №1: Поиск периода возрастания для квадратной функции

Рассмотрим пример квадратной функции f(x) = x2. Чтобы найти периоды возрастания и убывания этой функции, сначала найдем точки экстремума.
Для начала, найдем производную функции f'(x):
f'(x) = 2x
Чтобы определить, где производная равна нулю, решим уравнение f'(x) = 0:
2x = 0
Отсюда получаем, что x = 0 является единственной точкой экстремума данной функции.
Теперь проведем тестирование точки экстремума, а также интервалы до и после нее, чтобы определить, является ли данная точка экстремума максимумом или минимумом функции.
Возьмем случайное значение, например, x = -1, и подставим его в исходную функцию:
f(-1) = (-1)2 = 1
Теперь возьмем значение x = 1 и также подставим его в исходную функцию:
f(1) = (1)2 = 1
Из полученных значений видно, что функция имеет минимум в точке x = 0, так как значения до и после этой точки больше либо равны 1.
Таким образом, период возрастания функции f(x) = x2 равен промежутку между минимальными значениями функции, то есть период возрастания в данном случае не существует.
Алгоритм поиска периода убывания функции
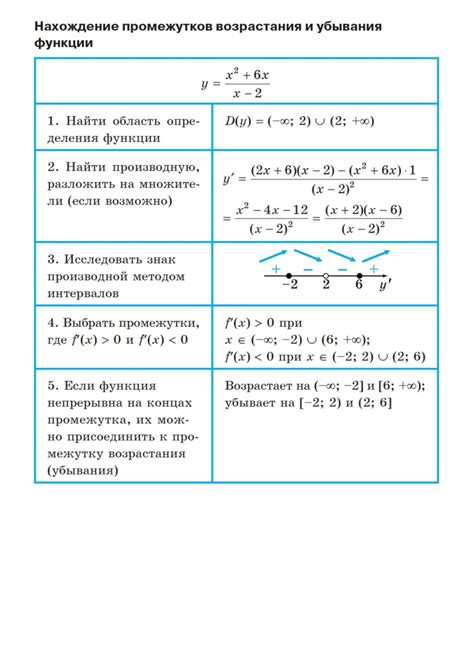
Для того чтобы найти периоды убывания функции, следуйте следующим шагам:
- Вычислите производную функции. Это позволит вам найти точки, в которых функция убывает.
- Найдите критические точки, в которых производная функции равна нулю или не существует. Это могут быть точки, в которых функция меняет свой характер с возрастания на убывание.
- Проверьте изменение знака производной функции между критическими точками и на краях области определения функции. Если производная меняет знак с положительного на отрицательный, это указывает на период убывания функции.
- Запишите полученные периоды убывания функции в нужной форме, указывая интервалы или конкретные значения переменной.
Пример:
Рассмотрим функцию f(x) = x^2 - 3x. Чтобы найти периоды убывания этой функции, сначала найдем производную:
f'(x) = 2x - 3
Найдем критическую точку, где f'(x) = 0:
2x - 3 = 0
2x = 3
x = 3/2
Проверим изменение знака производной между -∞ и 3/2, а также между 3/2 и +∞:
Выберем точку x = 0:
f'(0) = 2(0) - 3 = -3 < 0, производная отрицательна
Выберем точку x = 2:
f'(2) = 2(2) - 3 = 1 > 0, производная положительна
Значит, функция f(x) убывает на интервале (-∞, 3/2].
Записывая результаты, мы можем сказать, что функция f(x) убывает на интервале (-∞, 3/2].
Пример №2: Поиск периода убывания для тригонометрической функции
Рассмотрим функцию f(x) = sin(x). Необходимо найти периоды убывания данной функции.
Чтобы найти период убывания функции, следует сначала найти экстремумы функции, а затем промежутки между ними.
Так как функция sin(x) имеет период T = 2π, достаточно исследовать период [-π, π].
Для начала найдем экстремумы функции f(x) = sin(x) на заданном интервале. Запишем производную функции и приравняем ее к нулю:
ƒ'(x) = cos(x)
cos(x) = 0
x = π/2 + kπ
Где k - любое целое число.
Таким образом, экстремумы функции расположены в точках: x = -π/2 + kπ и x = π/2 + kπ.
Рассмотрим промежутки между экстремумами на заданном интервале. Для точек x = -π/2 + kπ и x = π/2 + kπ периодичность будет сохраняться.
| Промежуток | Признак |
|---|---|
| [-π, -π/2] | Убывание |
| [-π/2, π/2] | Убывание |
| [π/2, π] | Убывание |
Таким образом, функция f(x) = sin(x) убывает на интервалах [-π, -π/2], [-π/2, π/2] и [π/2, π].
Дополнительные советы для поиска периодов

Помимо основных методов анализа функций, есть несколько дополнительных приемов, которые помогут вам найти периоды возрастания и убывания функции.
Анализ производных
Одним из эффективных способов определить периоды возрастания и убывания функции является анализ ее производной. Положительные значения производной указывают на период возрастания функции, а отрицательные значения – на период убывания. Точки экстремума (максимумы и минимумы) производной соответствуют точкам пересечения этой функции с осью абсцисс.
Найдите производную функции, используя правила дифференцирования, и определите, где она положительна, а где отрицательна. Эти интервалы соответствуют периодам возрастания и убывания исходной функции.
Анализ знаков
Еще один способ найти периоды возрастания и убывания функции – анализ знаков выражения, определяющего функцию. Рассмотрите интервалы, где это выражение положительно, нулевое или отрицательное. Положительные интервалы соответствуют периодам возрастания, отрицательные – периодам убывания.
Пример:
Рассмотрим функцию f(x) = x^2 - 6x + 8. Найдем ее производную:
f'(x) = 2x - 6
Найдем точки, где производная равна нулю:
2x - 6 = 0
x = 3
Теперь разбиваем ось абсцисс на интервалы, используя найденные точки:
Область I: x < 3
Область II: x > 3
Анализируем знак производной на каждом интервале:
В области I: f'(x) < 0
В области II: f'(x) > 0
Следовательно, функция возрастает на интервале x > 3 и убывает на интервале x < 3.
Используйте эти методы и приведенный пример для эффективного анализа функций и нахождения их периодов возрастания и убывания.