Окружность - одна из основных геометрических фигур, привлекающая внимание своей красотой и простотой. Но иногда возникает необходимость определить, принадлежит ли точка к заданной окружности. Существует простой и эффективный способ выполнить данную задачу, который мы рассмотрим в данной статье.
Для начала необходимо понять основные понятия, связанные с окружностью. Радиус - это расстояние от центра окружности до любой ее точки. Диаметр - это двоякое расстояние между любыми двумя точками на окружности, проходящими через центр. И наконец, сама точка - это узкое понятие, представляющее собой объект с нулевыми размерами.
Теперь перейдем к процессу определения принадлежности точки к окружности. Нам понадобятся координаты центра окружности (Cx, Cy) и радиус R. Используя эти значения и координаты проверяемой точки (Px, Py), мы можем применить простую формулу. Учитывая, что точка (Px, Py) принадлежит окружности, если выполняется условие (Px - Cx)^2 + (Py - Cy)^2 = R^2.
Как определить принадлежность точки к окружности - простой способ
- Запишите уравнение окружности в виде (x - a)^2 + (y - b)^2 = r^2, где (a, b) - координаты центра окружности, r - радиус окружности.
- Запишите координаты проверяемой точки в виде (x0, y0).
- Подставьте значения координат точки в уравнение окружности и вычислите. Если полученное значение равно r^2, то точка лежит на окружности. Если значение меньше r^2, то точка лежит внутри окружности. Если значение больше r^2, то точка лежит вне окружности.
Приведенный способ предоставляет простое решение задачи определения принадлежности точки к окружности. Он основан на использовании уравнения окружности и координат точки. Данный метод может быть использован в различных геометрических задачах, связанных с окружностями.
Геометрическое понятие окружности и точки
Важным геометрическим понятием является точка, которая является базовым элементом в пространстве. Точка не имеет размеров, она представляет собой некую математическую абстракцию. В геометрии точки используются для указания местоположения объектов и решения различных задач.
Для определения принадлежности точки к окружности необходимо вычислить расстояние от данной точки до центра окружности и сравнить его с радиусом окружности. Если расстояние равно радиусу окружности, то точка принадлежит окружности, в противном случае – точка вне окружности.
Необходимые данные для определения принадлежности точки к окружности

Для определения принадлежности точки к окружности необходимо иметь следующие данные:
1. Координаты центра окружности: обозначаются как (Cx, Cy), где Cx - координата по оси X, а Cy - координата по оси Y.
2. Радиус окружности (r): представляет собой расстояние от центра окружности до любой точки на окружности.
3. Координаты проверяемой точки (Px, Py): обозначаются как (Px, Py), где Px - координата по оси X, а Py - координата по оси Y.
Опираясь на эти данные, можно использовать специальные математические формулы для определения принадлежности точки к окружности. Важно учесть, что в данном методе принадлежность точки к окружности определяется с помощью вычисления расстояния от центра окружности до проверяемой точки и сравнения его с радиусом окружности.
Пример:
Пусть у нас есть окружность с центром (2, 3) и радиусом 5. Нам нужно определить, принадлежит ли точка (4, 2) этой окружности.
Мы можем использовать формулу расстояния между двумя точками:
d = √((Px - Cx)^2 + (Py - Cy)^2)
Подставив значения, получаем:
d = √((4 - 2)^2 + (2 - 3)^2)
d = √(2^2 + (-1)^2)
d = √(4 + 1)
d = √5
Пошаговая инструкция для определения принадлежности точки к окружности
Для начала, вам понадобится знать координаты центра окружности и радиус. Пусть центр окружности имеет координаты (x0, y0), а радиус равен r.
Шаг 1: Получите координаты точки, которую нужно проверить на принадлежность к окружности. Пусть точка имеет координаты (x, y).
Шаг 2: Вычислите расстояние между центром окружности и точкой с помощью формулы:
| Формула для расчета расстояния: |
|---|
| d = sqrt((x - x0)^2 + (y - y0)^2) |
| Расставим значения: |
| d = sqrt((x - x0)^2 + (y - y0)^2), gdzie |
| x0 - координата x центра окружности |
| y0 - координата y центра окружности |
Шаг 3: Если полученное расстояние d меньше или равно радиусу окружности r, то точка принадлежит окружности. В противном случае, точка лежит вне окружности.
Теперь вы знаете простой способ определения принадлежности точки к окружности. Можете использовать эту инструкцию в своих проектах, зная, что результат будет точным и надежным.
Шаг 1: Найдите радиус окружности по формуле
Прежде чем определить принадлежность точки к окружности, необходимо знать радиус этой окружности. Для нахождения радиуса окружности по формуле, нужно измерить расстояние от центра окружности до любой точки ее окружности.
Формула для нахождения радиуса окружности задается следующим образом:
Радиус = (Длина отрезка между центром окружности и точкой на окружности) / 2
Поэтому, чтобы найти радиус окружности:
- Выберите любую точку на окружности.
- Измерьте расстояние от центра окружности до выбранной точки.
- Полученную длину поделите на 2.
Таким образом, вы найдете радиус окружности, который позволит определить принадлежность точки к ней.
Шаг 2: Найдите расстояние от центра окружности до заданной точки
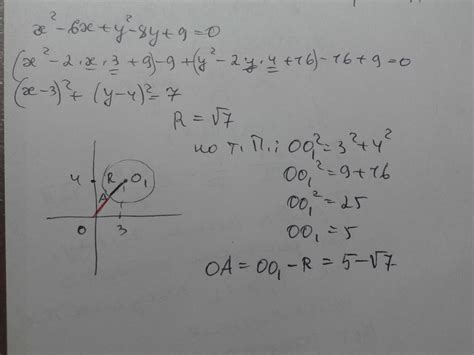
1. Для того чтобы определить принадлежность точки к окружности, необходимо найти расстояние от заданной точки до центра окружности.
2. Пусть координаты центра окружности равны (x0, y0), а координаты заданной точки - (x, y).
3. Расстояние между двумя точками можно вычислить с помощью формулы:
d = √((x - x0)2 + (y - y0)2)
4. Применяя данную формулу, подставьте значения координат центра окружности и заданной точки для расчета расстояния d.
5. Если полученное значение расстояния равно радиусу окружности, то заданная точка лежит на окружности. Если расстояние меньше радиуса, то точка находится внутри окружности. Если же расстояние больше радиуса, то точка находится вне окружности.
Шаг 3: Сравните полученное расстояние с радиусом окружности
- Возьмите значение радиуса окружности, которую нужно проверить, из существующих данных или расчетов.
- Сравните полученное расстояние от точки до центра окружности с радиусом.
Этот шаг позволяет принять окончательное решение о принадлежности точки к окружности, основываясь на свойствах геометрической фигуры. Сравнивая полученное расстояние и радиус, можно точно определить, находится ли точка на границе окружности или внутри нее.
Таблица ниже демонстрирует данную проверку:
| Расстояние от точки до центра | Радиус окружности |
|---|---|
| меньше или равно радиусу | Точка принадлежит окружности |
| больше радиуса | Точка не принадлежит окружности |
Для определения принадлежности точки к окружности необходимо учесть два важных условия:
- Координаты точки должны находиться на одинаковом расстоянии от центра окружности.
- Это расстояние должно быть равно радиусу окружности.
Если выполняются оба условия, то точка принадлежит окружности. В противном случае, точка не принадлежит окружности.
Для проверки условий можно воспользоваться известной формулой расстояния между двумя точками в координатной плоскости:
d = √((x2 - x1)^2 + (y2 - y1)^2)
Где (x1, y1) - координаты центра окружности, (x2, y2) - координаты проверяемой точки.
Если расстояние d равно радиусу окружности, то точка принадлежит окружности, иначе - не принадлежит.