Производная функции – это одна из основополагающих концепций математического анализа, которая позволяет определить скорость изменения функции в каждой точке графика. Она является инструментом для изучения поведения функции, ее экстремумов, монотонности и выпуклости.
Существует несколько способов нахождения производной функции, одним из которых является построение касательной к графику. Касательная к графику функции в определенной точке – это прямая, которая касается графика только в этой точке и имеет такой же наклон, как и сам график функции в этой точке.
Для нахождения производной функции по графику и касательной нужно использовать методы математического анализа, такие как пределы и асимптотические прямые. Однако, существуют и альтернативные способы для приближенного определения производной с использованием численных методов и графических инструментов.
Аналитический метод нахождения производной функции

Аналитический метод нахождения производной функции основан на использовании математических операций и правил дифференцирования. Этот метод позволяет найти точное значение производной функции в каждой точке её области определения.
Для того чтобы найти производную функции, необходимо последовательно применять следующие правила дифференцирования:
- Правило дифференцирования константы: производная любой константы равна нулю.
- Правило дифференцирования степенной функции: производная степенной функции равна произведению показателя степени на коэффициент перед степенью, а затем на функцию с показателем степени, уменьшенным на единицу.
- Правило дифференцирования суммы и разности функций: производная суммы или разности функций равна сумме или разности их производных.
- Правило дифференцирования произведения функций: производная произведения функций равна произведению производной первой функции на вторую функцию, и плюс произведение первой функции на производную второй функции.
- Правило дифференцирования частного функций: производная частного функций равна разности произведения производной первой функции на вторую функцию и произведения первой функции на производную второй функции, деленная на квадрат второй функции.
Применяя эти правила по очереди, можно найти производную функции в любой точке её области определения. Результатом будет функция, которая показывает скорость изменений и наклон касательной к графику функции в каждой точке.
Графический метод нахождения производной функции

Графический метод нахождения производной функции представляет собой один из способов определения значения производной в точке по графику функции.
Для применения данного метода необходимо иметь график функции, по которому можно провести касательную в нужной точке.
Для определения значения производной в точке с помощью графического метода следует выполнить следующие шаги:
- Найти на графике точку, в которой нужно найти производную.
- Провести касательную к графику функции в этой точке.
- Измерить угол наклона касательной к оси абсцисс.
- Выразить угол наклона касательной в виде отношения приращения значения функции к приращению аргумента.
- Полученное отношение является значением производной функции в данной точке.
Графический метод нахождения производной функции может быть полезен в ситуациях, когда аналитическое нахождение производной затруднено или невозможно. Однако следует помнить, что данный метод является приближенным и требует высокой точности измерений.
Касательная к графику функции и ее связь с производной
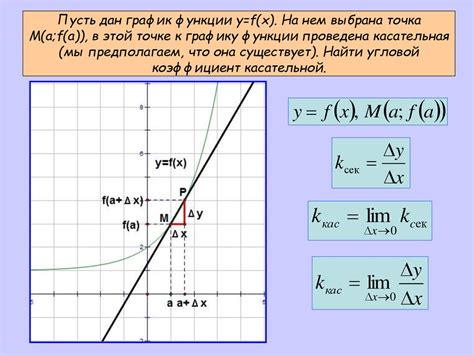
Существенную роль в определении касательной к графику функции играет производная. Производная функции – это показатель ее изменения в данной точке, а точнее, это тангенс угла наклона касательной к графику функции в этой точке.
Для нахождения касательной к графику функции первым шагом необходимо найти производную этой функции. Затем, используя найденную производную, найдем значение функции в данной точке. Это значение будет равно значению касательной в этой точке.
Для построения касательной к графику функции проходящей через точку меры x₀, необходимо использовать следующую формулу:
| Уравнение касательной: | y = f(x₀) + f'(x₀) * (x - x₀) |
|---|
В данной формуле, f(x₀) – значение функции в точке x₀, а f'(x₀) – значение производной функции в точке x₀.
Таким образом, производная функции позволяет нам определить наклон касательной к графику функции в каждой точке. Исследование наклона касательной к графику функции позволяет нам понять, как меняется функция и ее значения вблизи данной точки.
Правила нахождения производной функции по графику

Для нахождения производной функции по графику следует руководствоваться следующими правилами:
- Определить точку, в которой необходимо найти производную.
- Построить касательную к графику функции в этой точке.
- Определить наклон касательной. Если касательная является прямой линией, то наклон будет постоянным; если касательная представляет собой кривую, то наклон будет меняться в зависимости от положения точки на графике.
- Найти значение наклона касательной в данной точке. Это значение и будет являться производной функции в этой точке.
Для более точного определения производной функции по графику, рекомендуется проводить ряд измерений наклона касательной в различных точках. Также полезно применять дополнительные графические методы, например, использование касательных к соседним точкам для вычисления производной приближенно.
Использование графического метода для нахождения производной функции позволяет визуализировать аналитическое определение производной и дает возможность лучше понять ее свойства и особенности в конкретных точках графика.
Примеры нахождения производной функции по графику
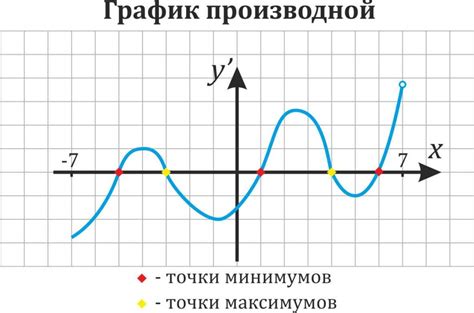
Рассмотрим несколько примеров нахождения производной функции по графику:
Пример 1:
Дан график функции y = f(x).
Чтобы найти производную функции f(x) в точке a, мы ищем тангенциальную прямую к графику в этой точке. Угловой коэффициент этой прямой будет равен значению производной функции в точке a.
Пример 2:
Дан график функции y = f(x).
Чтобы найти производную функции f(x) в точке b, мы определяем мгновенную скорость изменения функции в этой точке. Коэффициент наклона касательной к графику в точке b будет равен значению производной функции в этой точке.
Пример 3:
Дан график функции y = f(x).
Чтобы найти производную функции f(x) в точке c, мы смотрим на угловой коэффициент секущей прямой, проходящей через две точки графика, расположенные ближе всего к точке c. Если мы приблизим эти две точки друг к другу, то получим касательную к графику. Коэффициент наклона этой касательной будет равен значению производной функции в точке c.
Таким образом, нахождение производной функции по графику позволяет нам определить скорость изменения функции и найти касательную к графику в определенной точке. Это является важным инструментом для анализа и понимания поведения функций.
Применение производной функции в задачах с графиком
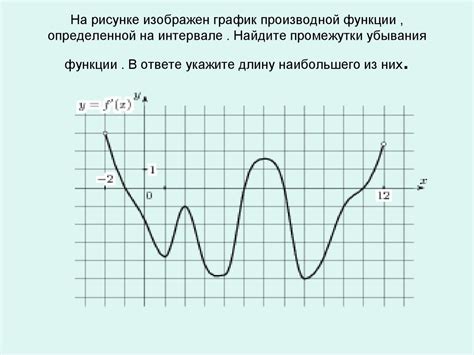
1. Определение экстремумов функции. График функции может иметь точки, в которых производная равна нулю или не существует. Такие точки называются критическими точками. Используя производную функции, можно найти эти точки и определить, являются ли они точками максимума или минимума функции.
2. Построение касательной. Производная функции в точке представляет собой наклон касательной к графику функции в этой точке. Используя значение производной в определенной точке и зная координаты этой точки, можно построить уравнение касательной и найти ее угловой коэффициент.
3. Определение направления изменения функции. Знак производной функции в определенной точке указывает на направление изменения функции в этой точке. Если производная положительна, то функция возрастает, если отрицательна - функция убывает. Таким образом, производная функции позволяет анализировать поведение функции на различных участках ее графика.
4. Решение оптимизационных задач. Используя производную функции, можно решать различные оптимизационные задачи, например, нахождение максимального или минимального значения функции при заданных условиях.
Применение производной функции в задачах с графиком позволяет более глубоко анализировать функции и находить оптимальные решения. Это важный инструмент как в математике, так и во многих других областях, таких как экономика, физика, инженерия и т.д.
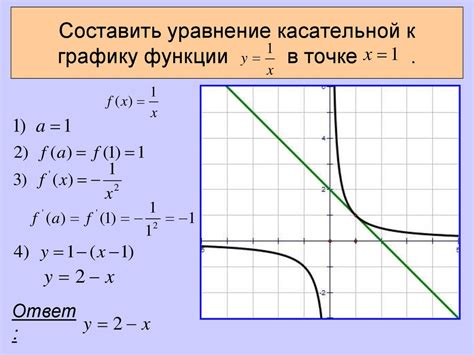
Решение задач на поиск касательной к графику функции

При решении задач на поиск касательной к графику функции необходимо учитывать несколько важных шагов. Прежде всего, нужно определить точку, в которой требуется найти касательную. Это может быть заданная точка или точка с известными координатами.
Далее следует вычислить производную функции с помощью правила дифференцирования. Производная в точке будет являться угловым коэффициентом касательной к графику функции в этой точке.
После вычисления производной необходимо записать уравнение касательной в виде y = kx + b, где k - угловой коэффициент и b - значение функции в заданной точке.
Для определения значения функции в заданной точке можно использовать предопределенную формулу или подставить значения координат точки в исходное уравнение функции.
Важно учесть, что при подсчете производной и записи уравнения касательной необходимо строго соблюдать алгоритм действий и правила дифференцирования. Несоблюдение этих правил может привести к ошибкам в решении задачи.
Для наглядного представления решения задачи на поиск касательной можно использовать таблицу с промежуточными вычислениями и результатами. В таблице следует указать значения координат точки, производную функции и уравнение касательной.
| Точка | Значение функции | Производная | Уравнение касательной |
|---|---|---|---|
| (x, y) | f(x) | f'(x) | y = f'(x) * x + b |
В итоге, решение задачи на поиск касательной к графику функции включает определение точки, вычисление производной, запись уравнения касательной и наглядное представление решения в виде таблицы с промежуточными вычислениями.
Применение касательной к графику функции в задачах
Одной из основных задач, которую можно решить с помощью касательной, - определение значения производной функции в заданной точке. Производная функции в данной точке показывает скорость изменения функции в этой точке, то есть ее тангенс угла наклона. Определение производной функции позволяет получить информацию о поведении функции в окрестности данной точки.
Кроме того, использование касательной позволяет находить экстремумы функции - минимумы и максимумы. Экстремумы функции соответствуют точкам, в которых ее производная равна нулю или не существует. График функции при этом пересекает касательную в этих точках.
Другой задачей, которую можно решить с помощью касательной, - аппроксимация функции. Аппроксимация позволяет приближенно описать функцию с помощью прямой, проходящей через заданную точку на графике. Касательная в этой точке является линейной аппроксимацией функции и может быть использована для прогнозирования значений функции вблизи заданной точки.
Таким образом, применение касательной к графику функции позволяет решать различные задачи, связанные с анализом и интерпретацией функций. Знание алгоритма нахождения касательной и свойств производной функции поможет в решении этих задач и расширит понимание основ математики.


