В физике колебаний важную роль играет определение пути с известной амплитудой и периодом колебаний. Это позволяет предсказывать движение объекта и анализировать его характеристики. Существуют различные способы определения пути, однако наиболее распространенными являются формула и методы расчета.
Одна из основных формул, использованных при расчете пути с известной амплитудой и периодом колебаний, - это формула гармонического колебания. Она выглядит следующим образом: x(t) = A * sin(2 * π * f * t), где x - путь, A - амплитуда, f - частота, t - время.
Методы расчета предполагают использование данной формулы и проведение математических операций для определения пути. Важно учесть, что путь будет меняться со временем и максимален при максимальном значении амплитуды.
Итак, путь с известной амплитудой и периодом колебаний можно определить с использованием формулы гармонического колебания и методов расчета. Это позволяет не только предсказывать движение объекта, но и анализировать его характеристики, что является важным для многих областей физики, техники и естественных наук.
Методы расчета пути с известной амплитудой и периодом колебаний
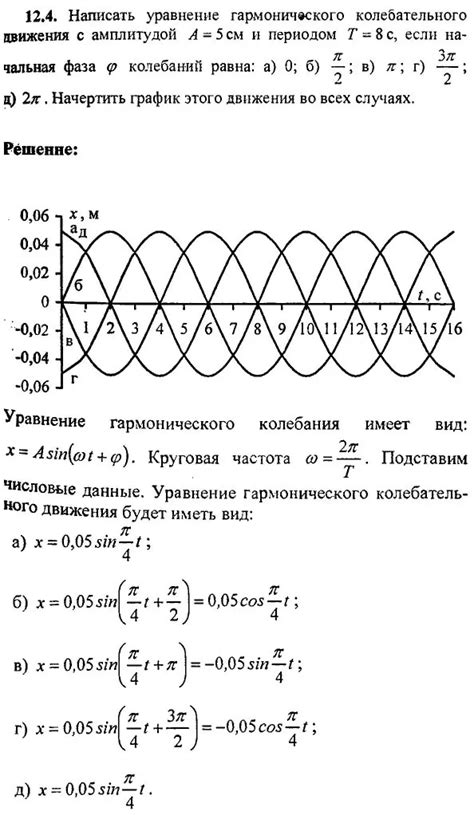
Для определения пути с известной амплитудой и периодом колебаний существуют различные методы расчета. В этом разделе рассмотрим несколько наиболее распространенных методов.
1. Метод гармонического анализа
Метод гармонического анализа основан на разложении сложного движения на гармонические колебания различных частот. Пусть у нас есть функция, описывающая движение с известной амплитудой и периодом колебаний. С помощью метода гармонического анализа мы можем разложить эту функцию на сумму гармонических компонент с различными амплитудами и частотами. Затем, зная амплитуды и фазы каждой из гармонических компонент, можно определить путь, который будет соответствовать исходному движению.
2. Метод численного интегрирования
Другим распространенным методом расчета пути с известной амплитудой и периодом колебаний является метод численного интегрирования. Идея этого метода заключается в том, чтобы численно интегрировать уравнение движения для получения зависимости координаты от времени. При этом используется метод Эйлера или другие методы численного интегрирования. Результатом работы метода является последовательность значений координаты, от которых можно построить график пути.
3. Метод аналитического решения уравнений движения
Некоторые простые системы могут быть решены аналитически - то есть найти явное выражение для пути с известной амплитудой и периодом колебаний. Например, для гармонического осциллятора с известной силой и начальными условиями можно решить уравнение движения и получить явное выражение для пути. Этот метод особенно полезен для систем с простыми уравнениями движения, которые можно решить аналитически.
Все эти методы имеют свои преимущества и недостатки, и выбор метода зависит от конкретной задачи. Важно учитывать, что точность результата может зависеть от выбранного метода, поэтому необходимо выбирать метод, подходящий для конкретной задачи и учитывать его ограничения.
Общая формула для определения пути колебаний

Общая формула для определения пути колебаний выглядит следующим образом:
- Для гармонических колебаний вида x = A*sin(ωt + φ)
- где x - смещение относительно положения равновесия,
- A - амплитуда колебаний,
- ω - циклическая частота колебаний,
- t - время,
- φ - начальная фаза колебаний.
Таким образом, путём колебаний будет представлять график функции y = A*sin(ωt + φ), где на оси абсцисс откладывается время t, а на оси ординат – значение смещения x.
Эта формула дает возможность определить путь колебаний для любого типа гармонических колебаний. Значения амплитуды, частоты и начальной фазы могут быть известными или определены экспериментально.
Формула пути в зависимости от амплитуды и периода колебаний
Для определения пути с известной амплитудой и периодом колебаний существует специальная формула, которая позволяет рассчитать это значение.
Формула пути зависит от амплитуды (A) и периода (T) колебаний и выглядит следующим образом:
S = A * sin(2πt / T)
Где:
- S - путь, который пройдет объект от начальной точки
- A - амплитуда колебаний, то есть максимальное отклонение объекта от равновесной позиции
- t - время, прошедшее с начала колебаний
- T - период колебаний, то есть время, за которое объект совершает одно полное колебание
Используя данную формулу, можно определить путь объекта в любой момент времени во время колебаний с известными амплитудой и периодом колебаний.
Важно отметить, что данный подход применим для гармонических колебаний, когда сила, действующая на объект, пропорциональна его отклонению от равновесной позиции.
Графический метод определения пути колебаний
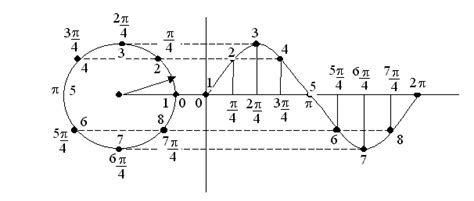
Для построения графика пути колебаний необходимо знать амплитуду и период колебаний. Амплитуда представляет собой максимальное удаление точки от положения равновесия, а период - время, за которое происходит одно полное колебание.
Построение графика пути колебаний осуществляется путем отложения времени по горизонтальной оси и положения точки по вертикальной оси. Затем, используя известные значения амплитуды и периода колебаний, можно построить кривую, представляющую путь колебаний.
| Время, с | Положение точки, м |
|---|---|
| 0 | 0 |
| T/4 | A |
| T/2 | 0 |
| 3T/4 | -A |
| T | 0 |
Для более точного построения графика пути колебаний можно увеличить количество точек, используя промежуточные значения времени и положения точки.
Графический метод определения пути колебаний является удобным способом визуализации движения материальной точки и позволяет получить представление о форме и характере колебаний. Он широко применяется в различных областях науки и техники, где требуется анализ периодических процессов.
Принцип работы графического метода расчета
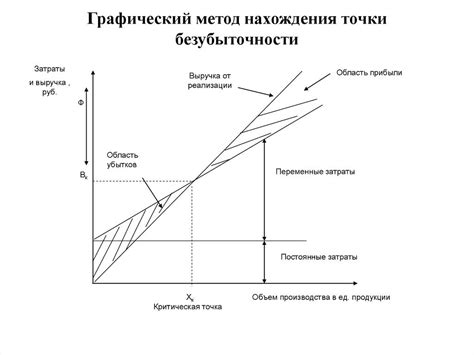
Графический метод расчета позволяет определить путь с известной амплитудой и периодом колебаний с помощью построения графика зависимости положения точки от времени. Этот метод основан на законе сохранения энергии в гармоническом осцилляторе.
Для начала необходимо выбрать систему координат и задать начальное условие – положение и скорость точки в начальный момент времени. Затем на основе уравнений движения можно определить уравнение пути точки в зависимости от времени.
Далее следует построить график зависимости положения точки от времени. Для этого нужно выбрать достаточное количество точек на интервале времени, равном периоду колебаний, и определить положение точки в каждый из этих моментов времени.
Полученные значения заносятся в таблицу, в которой первый столбец соответствует моменту времени, а второй – положению точки. Затем нужно построить график, где по горизонтальной оси откладывается время, а по вертикальной – положение точки.
Полученный график позволяет визуально определить амплитуду и период колебаний. Амплитуда равна расстоянию от положительной амплитуды до нулевого положения, а период – время, за которое точка совершает одно полное колебание. Величина амплитуды определяется по вертикальной оси, а период – по горизонтальной.
Графический метод расчета позволяет визуально наглядно представить движение точки и определить основные характеристики колебаний, что упрощает процесс расчета пути с известной амплитудой и периодом колебаний.
Метод численного расчета для определения пути колебаний
Помимо аналитического метода, существует также численный метод для расчета пути колебаний. В основе этого метода лежит использование численных методов интегрирования, таких как метод Эйлера или метод Рунге-Кутты. Эти методы позволяют приближенно находить значения функции в каждый момент времени и тем самым определить путь колебаний.
Процесс численного расчета пути колебаний состоит из следующих шагов:
- Выбор начального условия: определение начального значения координаты и скорости объекта в начальный момент времени
- Выбор шага по времени: определение интервала времени, на котором будут расчитываться значения функции
- Использование численных методов интегрирования: для каждого шага по времени вычисляются новые значения координаты и скорости объекта на основе предыдущих значений и известной функции ускорения
- Повторение шага 3 для каждого последующего шага по времени до достижения конечного момента времени
Использование численного метода позволяет моделировать колебания с высокой точностью, особенно в случаях, когда аналитическое решение не имеется или трудно получить. Однако, такой метод требует больше вычислительных ресурсов и времени выполнения, поэтому выбор между аналитическим и численным методом зависит от конкретной задачи и доступных ресурсов.
Применение численного метода для различных типов колебаний
Один из наиболее распространенных численных методов - метод Эйлера. Он основан на аппроксимации итерационной формулой, которая позволяет определить положение системы на следующем временном шаге исходя из текущего положения и скорости. Этот метод обычно применяется для колебаний с постоянной амплитудой и периодом.
Для колебаний с переменной амплитудой и периодом необходимо использовать более сложные численные методы, такие как метод Рунге-Кутты или метод Фейнберга. Они позволяют учесть изменение амплитуды и периода в процессе колебаний, что делает их применимыми для более реалистичного моделирования многих систем.
Благодаря численным методам, исследователи и инженеры могут изучать различные типы колебаний и определять их параметры на основе имеющихся данных. Это позволяет разрабатывать более точные модели систем и улучшать их производительность и надежность.
Однако следует помнить, что численные методы требуют точных начальных данных и правильного выбора параметров. Также они не всегда могут дать точное аналитическое решение, поэтому они должны быть использованы с осторожностью и проверены на корректность результаты.
В целом, применение численного метода для различных типов колебаний является неотъемлемой частью исследований в области физики, инженерии и науки о материалах. Этот метод позволяет получить более глубокое понимание колебаний и создавать точные модели систем, что имеет важное значение в различных приложениях.