Радиус круга - одна из основных характеристик данной фигуры, которая отражает расстояние от центра круга до его окружности. Зная периметр трапеции, можно вычислить радиус вписанного в нее круга. Это интригующее математическое задание требует определенных действий и опыта. Итак, мы сейчас узнаем, как это сделать.
Первым шагом в решении данной задачи является определение понятия вписанного круга. Это круг, который касается всех сторон трапеции внутренними точками. У него особенные свойства и характеристики, одна из которых и является радиус.
Чтобы найти радиус круга через периметр трапеции, нам необходимо знать формулу для нахождения радиуса вписанного круга в треугольник. Так как трапеция является особым типом треугольника, мы можем воспользоваться данными знаниями для расчета радиуса.
Для вычисления радиуса круга, примем во внимание основную формулу, связывающую радиус вписанного круга и периметр трапеции. Существует несколько способов решения данной задачи, и все они позволяют получить схожий результат - радиус круга через периметр трапеции. Следуя этим формулам и осознавая весь процесс расчетов, вы сможете с легкостью найти ответ на эту задачу.
Формула расчета радиуса круга через периметр трапеции

Если известен периметр трапеции и требуется найти радиус круга, описанного вокруг этой трапеции, можно воспользоваться следующей формулой:
- Найдите длины оснований трапеции.
- Сложите длины оснований и умножьте полученную сумму на 0.5.
- Полученный результат будет равен длине средней линии трапеции.
- Введите значение периметра трапеции в формулу:
- Где a, b, c, d - длины сторон трапеции.
- Раскройте скобки и перенесите слагаемые в другую сторону уравнения, чтобы найти значение радиуса, выразив его через периметр:
- Зная значение d (длины средней линии трапеции), радиус круга можно найти, разделив d на 2pi, где pi - математическая константа, близкая к 3.14.
P = 2 * (a + b + c + d)
P/2 - a - b - c = d
Таким образом, формула для расчета радиуса круга через периметр трапеции имеет вид:
r = d/(2 * pi)
Полученное значение радиуса будет радиусом круга, описанного вокруг трапеции.
Определение периметра трапеции

Для определения периметра трапеции нужно сложить длины всех четырех сторон. Если основания трапеции равны, то периметр можно найти так: P = a + b + 2c, где a и b – длины равных оснований, а c – длина боковой стороны.
Если основания трапеции не равны, то периметр можно найти так: P = a + b + c + d, где a и b – длины оснований, а c и d – длины боковых сторон.
Периметр трапеции позволяет определить длину внешней границы фигуры, что может быть полезно при решении различных геометрических задач.
| Тип трапеции | Периметр |
|---|---|
| Равнобедренная трапеция | P = a + b + 2c |
| Произвольная трапеция | P = a + b + c + d |
Связь периметра трапеции с радиусом круга
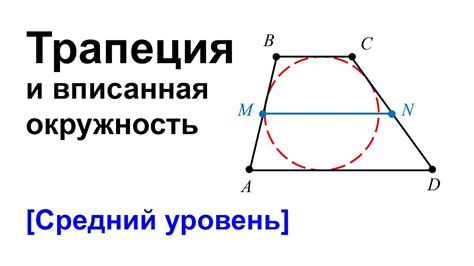
Если знаем периметр трапеции, то можем использовать эту информацию для определения радиуса круга, вписанного в эту трапецию. Внутри трапеции, вписанного круга, все точки на окружности касаются сторон трапеции.
Существует формула, позволяющая выразить радиус круга через периметр трапеции:
- Вычислим основание трапеции, сложив длины оснований и разделив на 2.
- Найдем высоту трапеции, используя формулу площади трапеции: площадь равна произведению высоты на среднюю линию.
- Периметр равен сумме всех сторон, то есть двух оснований и двух боковых сторон. Основания трапеции уже известны, осталось найти длину боковых сторон. Для этого можно использовать теорему Пифагора, так как боковая сторона - это гипотенуза прямоугольного треугольника.
- Получив все значения сторон, подставим их в формулу площади треугольника, найдя площадь боковой стороны.
- Далее, воспользуемся формулой площади прямоугольника для нахождения площади основания трапеции.
- Используем найденные значения площадей боковой стороны и основания трапеции для нахождения радиуса вписанного круга по формуле радиус круга равен квадратному корню из отношения площади основания к площади боковой стороны.
Таким образом, зная периметр трапеции, можно найти радиус вписанного круга при помощи вышеуказанной формулы. Это позволяет связать эти две величины и упростить расчеты при выполнении геометрических задач.