Окружность – это геометрическая фигура, состоящая из всех точек плоскости, равноудалённых от данной точки, называемой центром окружности. Радиус окружности – это расстояние от центра окружности до любой ее точки. В физике знание радиуса окружности может быть необходимо в различных ситуациях, особенно в задачах, связанных с движением тел.
Как найти радиус окружности в физике для 10 класса? Возможно, тебе знакома формула для вычисления длины окружности, где L обозначает длину окружности, а r – радиус. Формула звучит так: L = 2πr. Если тебе известна длина окружности, то можешь легко найти радиус, подставив известные значения в данную формулу.
Предположим, у нас есть задача: длина окружности равна 10 метрам. Как найти радиус этой окружности? Подставим значения в формулу: 10 = 2πr. Чтобы найти неизвестный радиус, разделим обе части уравнения на 2π. Получим уравнение r = 10/(2π). Подставим значение π (приближенно равно 3.14) в это уравнение и выполним вычисления. Таким образом, радиус данной окружности составляет примерно 1.59 метра.
Что такое радиус окружности?
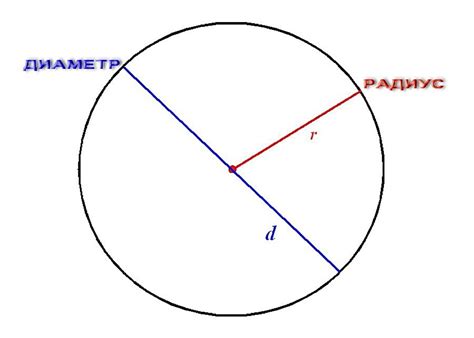
Радиус является одним из основных понятий геометрии и широко используется в различных областях науки и техники, включая физику. В физике радиус окружности имеет важное значение при расчетах пути, скорости и ускорения движения тела по окружности.
Радиус окружности связан с другими ее характеристиками.
- Диаметр (D) окружности - это отрезок, соединяющий две ее точки на противоположных сторонах и проходящий через центр окружности. Диаметр равен удвоенному значению радиуса: D = 2r.
- Длина окружности (L) - это периметр окружности, равный удвоенному произведению пи (π) на радиус: L = 2πr.
- Площадь круга (S) - это площадь, ограниченная окружностью. Площадь круга равна квадрату радиуса, умноженному на число пи: S = πr².
Знание радиуса позволяет проводить различные расчеты и анализировать свойства окружности. Он имеет фундаментальное значение в геометрии и позволяет определить характеристики окружности, такие как ее длина, площадь и взаимосвязь с другими геометрическими фигурами.
Определение радиуса окружности

Если известна длина окружности, радиус можно найти, используя формулу:
r = c / (2π)
где r - радиус окружности, c - длина окружности, π - математическая константа, приближенно равная 3.14.
Если известна площадь круга, радиус будет найден с использованием формулы:
r = √(S / π)
где r - радиус окружности, S - площадь круга, π - математическая константа, приближенно равная 3.14.
Если известен диаметр окружности, радиус будет определен как половина диаметра:
r = d / 2
где r - радиус окружности, d - диаметр окружности.
Таким образом, зная одну из указанных величин, можно определить радиус окружности, что позволит лучше понять ее геометрические свойства и использовать в необходимых физических расчетах.
Формула для расчета радиуса окружности
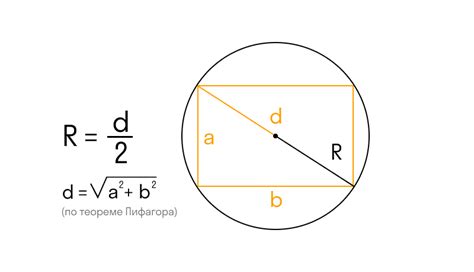
Если известна длина окружности (L), то радиус (R) может быть найден с помощью следующей формулы:
R = L / (2π)
где π (пи) представляет собой математическую константу, приближенно равную 3,14159. Эта формула позволяет нам вычислять радиус окружности при известной длине.
Если длина окружности неизвестна, но заданы явные геометрические данные, такие как касательные или хорды, радиус окружности может быть найден с помощью различных геометрических методов, таких как теорема Пифагора или теорема о касательной.
Примеры задач на нахождение радиуса окружности
Ниже приведены примеры задач, в которых необходимо найти радиус окружности.
Пример 1:
Дана окружность с диаметром равным 10 сантиметрам. Найдите радиус данной окружности.
Решение:
Диаметр окружности равен удвоенному радиусу, поэтому радиус окружности будет равен половине диаметра:
Радиус = Диаметр / 2 = 10 см / 2 = 5 см
Пример 2:
Известно, что длина окружности равна 12 сантиметрам. Найдите радиус данной окружности.
Решение:
Формула для нахождения длины окружности:
Длина = 2 * π * Радиус
Зная, что длина окружности равна 12 сантиметрам, можем решить уравнение:
2 * π * Радиус = 12 см
Радиус = 12 см / (2 * π) ≈ 1,91 см
Пример 3:
В задаче измеряются длины отрезков, соединяющих точки на окружности. Найдите радиус окружности, если известно, что длина отрезка, соединяющего центр окружности и точку на окружности, равна 8 сантиметрам.
Решение:
Длина отрезка, соединяющего центр окружности и точку на окружности, равна радиусу окружности:
Радиус = 8 см
Пример 4:
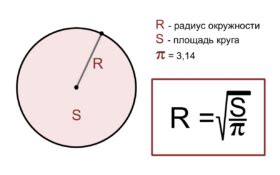
Известно, что площадь круга равна 25 π квадратных сантиметров. Найдите радиус окружности.
Решение:
Формула для нахождения площади круга:
Площадь = π * Радиус^2
Зная, что площадь круга равна 25 π квадратных сантиметров, можем решить уравнение:
25 π = π * Радиус^2
Радиус^2 = 25
Радиус = √25 = 5 см
Эти примеры задач помогут вам разобраться в способах нахождения радиуса окружности в физике для 10 класса.