Определение ранга матрицы является важным инструментом в линейной алгебре и находит широкое применение в различных областях, включая физику, экономику и компьютерные науки. Ранг матрицы - это число линейно независимых строк или столбцов в матрице. Определить ранг матрицы можно различными способами, одним из которых является использование определителя матрицы.
Определитель матрицы является числовой характеристикой, которая позволяет определить некоторые свойства матрицы. Для квадратной матрицы определитель равен произведению элементов главной диагонали матрицы, умноженному на (-1) в степени, равной сумме номеров строки и столбца элемента, чей определитель рассчитывается. Если определитель равен нулю, то матрица является вырожденной и ее ранг равен нулю. Если определитель не равен нулю, то матрица невырожденная и ее ранг равен количеству линейно независимых строк или столбцов.
Для наглядного понимания процесса определения ранга матрицы через определитель рассмотрим пример. Пусть дана матрица A размером 3x3:
| 1 2 3 | | 4 5 6 | | 7 8 9 |
Чтобы определить ранг этой матрицы, необходимо рассчитать ее определитель. Раскладываем матрицу по первой строке и получаем следующее выражение:
| 1 2 3 | | 4 5 6 | | 7 8 9 |
= 1 * (5 * 9 - 6 * 8) - 2 * (4 * 9 - 6 * 7) + 3 * (4 * 8 - 5 * 7) = 1 * (-3) - 2 * (-6) + 3 * (-3) = -3 + 12 - 9 = 0.
Таким образом, определитель матрицы A равен нулю, что говорит о ее вырожденности. Следовательно, ранг данной матрицы также равен нулю. Этот пример демонстрирует, что для определения ранга матрицы через определитель необходимо рассчитать значение определителя и проверить, равен ли он нулю.
Что такое ранг матрицы?

Определение ранга матрицы можно упростить следующим образом: ранг матрицы равен размерности линейной оболочки ее строк (или столбцов). Линейная оболочка представляет собой множество всех линейных комбинаций векторов.
Ранг матрицы может быть определен с помощью элементарных преобразований над строками или столбцами матрицы. Определитель матрицы также может быть использован для определения ее ранга. В частности, если определитель матрицы отличен от нуля, то ранг матрицы равен количеству ее строк (или столбцов).
Понимание ранга матрицы играет важную роль при решении систем линейных уравнений. Например, система линейных уравнений с матрицей, чей ранг меньше числа переменных, имеет бесконечно много решений или не имеет решений вовсе.
Ранг матрицы также связан с понятием линейной зависимости. Если ранг матрицы равен числу ее строк (или столбцов), то строки (или столбцы) матрицы линейно независимы. В противном случае, если ранг матрицы меньше числа ее строк (или столбцов), то матрица содержит линейно зависимые строки (или столбцы).
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Определение и основные понятия
Матрица - это прямоугольная таблица чисел, разделенных на строки и столбцы. Размерность матрицы определяется числом строк и столбцов.
Для определения ранга матрицы через определитель необходимо выполнить следующие шаги:
- Выбрать квадратную подматрицу данной матрицы, у которой отличны от нуля определители, исключая при этом все остальные строки и столбцы.
- Вычислить определитель выбранной подматрицы. Если определитель отличен от нуля, то ранг матрицы равен числу строк и столбцов выбранной подматрицы.
- Если определитель выбранной подматрицы равен нулю, то перейти к следующей подматрице с меньшим числом строк и столбцов и повторить шаги 1 и 2 до тех пор, пока не будет найдена подматрица с ненулевым определителем.
- Ранг матрицы равен числу строк и столбцов найденной подматрицы с ненулевым определителем.
Определение ранга матрицы через определитель позволяет эффективно вычислить ранг больших матриц и применяется в различных областях, включая теорию систем, машинное обучение и обработку изображений.
Как найти определитель матрицы?

Существует несколько способов нахождения определителя матрицы, однако один из наиболее распространенных методов - это использование разложения матрицы по строке или столбцу.
Разложение матрицы по строке представляет собой следующий алгоритм:
- Выбираем любую строку матрицы.
- Для каждого элемента этой строки вычисляем его алгебраическое дополнение - это минор данного элемента, умноженный на (-1) в степени суммы номера строки и столбца.
- Суммируем произведения элементов строки на их алгебраические дополнения.
Разложение матрицы по столбцу проводится аналогично, только выбирается столбец, а элементы суммируются с учетом алгебраических дополнений столбца.
Также можно использовать свойства определителей, такие как разложение по строке/столбцу на два определителя меньшего размера, определитель транспонированной матрицы, определитель произведения матриц и другие.
Пример:
Рассмотрим матрицу A:
2 5 1
3 7 2
4 8 6
Найдем определитель этой матрицы, используя разложение по первой строке:
2 5 1
3 7 2
4 8 6
Вычисляем алгебраическое дополнение для элемента 2:
7 2
8 6
Алгебраическое дополнение для элемента 2 равно -26.
Вычисляем алгебраическое дополнение для элемента 5:
3 2
4 6
Алгебраическое дополнение для элемента 5 равно 6.
Вычисляем алгебраическое дополнение для элемента 1:
3 7
4 8
Алгебраическое дополнение для элемента 1 равно 4.
Вычисляем определитель матрицы:
2 5 1
3 7 2
4 8 6
Определитель матрицы A равен 2*(-26) + 5*6 + 1*4 = -48 + 30 + 4 = -14.
Таким образом, определитель матрицы A равен -14.
Алгоритм вычисления определителя
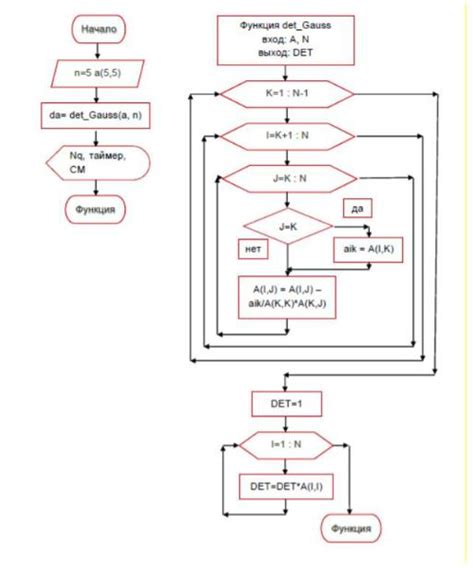
Вычисление определителя матрицы может быть выполнено с помощью специального алгоритма. Вот основные шаги этого алгоритма:
- Проверить размерность матрицы. Определитель может быть вычислен только для квадратной матрицы, то есть матрицы, у которой количество строк равно количеству столбцов.
- Разложить матрицу на дополнительные миноры. Дополнительный минор - это минор, полученный удалением одной строки и одного столбца из исходной матрицы. Обычно используется разложение по первой строке или столбцу.
- Вычислить определитель каждого дополнительного минора.
- Сложить (или вычесть) эти определители с определенными знаками. Знаки определителей чередуются в зависимости от позиции дополнительного минора в исходной матрице. Например, определитель минора находящегося в позиции (i,j) будет иметь знак (-1)^(i+j).
- Получить искомое значение определителя как сумму (или разность) всех определителей дополнительных миноров.
Например, рассмотрим квадратную матрицу размерностью 3x3:
| 1 2 3 | | 4 5 6 | | 7 8 9 |
Мы можем разложить эту матрицу на дополнительные миноры, используя первую строку:
| X X X | | 4 5 6 | | 7 8 9 |
| 1 2 3 | | X X X | | 7 8 9 |
| 1 2 3 | | 4 5 6 | | X X X |
Затем вычислим определитель каждого минора:
Дополнительный минор 1: 1*(5*9 - 6*8) = -3 Дополнительный минор 2: 4*(2*9 - 3*8) = 24 Дополнительный минор 3: 7*(2*6 - 3*5) = -9Наконец, сложим эти определители с определенными знаками:
Определитель = -3 + 24 - 9 = 12Таким образом, определитель данной матрицы равен 12.
Как определить ранг матрицы?

Для определения ранга матрицы нужно выполнить следующие шаги:
- Найти определитель матрицы.
- Проверить каждый минор матрицы. Минор - это матрица, полученная из матрицы путем вычеркивания одной или нескольких строк и столбцов.
- Если определитель минора отличен от нуля, то он считается ненулевым минором.
- Посчитать количество ненулевых миноров.
Количество ненулевых миноров является рангом матрицы. Если ранг матрицы равен n, то матрица называется полноранговой. Если ранг матрицы меньше n, то она называется неполноранговой.
Пример:
| 2 | 4 | 6 |
| 1 | 3 | 5 |
| 3 | 6 | 9 |
Из данной матрицы можно получить следующие ненулевые миноры:
| 2 |
| 2 | 4 |
| 1 | 3 |
Таким образом, ранг данной матрицы равен 2, так как имеет два ненулевых минора.
Связь ранга и определителя

Если матрица имеет ранг, равный нулю, то её определитель также будет равен нулю. Это происходит, когда все строки или столбцы матрицы линейно зависимы друг от друга, то есть можно выразить один из них через линейную комбинацию остальных.
Если ранг матрицы равен её порядку (например, равен количеству строк или столбцов), то определитель такой матрицы будет отличен от нуля. Это происходит, когда все строки или столбцы матрицы линейно независимы друг от друга, то есть невозможно выразить одну строку или столбец через линейную комбинацию остальных.
Таким образом, связь между рангом матрицы и её определителем позволяет использовать один из этих показателей для определения другого. Если мы знаем ранг матрицы, то можем судить о её определителе, и наоборот.
| Пример | Ранг матрицы | Определитель матрицы |
|---|---|---|
| Матрица A | 2 | 0 |
| Матрица B | 3 | 6 |
| Матрица C | 4 | 24 |
В примере выше видно, что если ранг матрицы равен нулю, то определитель такой матрицы будет равен нулю. Если ранг равен порядку матрицы, то определитель будет ненулевым числом.
Пошаговое объяснение определения ранга матрицы

Для определения ранга матрицы можно использовать определитель матрицы. Давайте рассмотрим пошаговое объяснение этого процесса:
- Начните с исходной матрицы, для которой нужно определить ранг.
- Приведите матрицу к ступенчатому виду, используя элементарные преобразования строк. Это значит, что каждая следующая строка матрицы должна начинаться с большего числа нулей, чем предыдущая строка.
- Подсчитайте количество ненулевых строк в ступенчатом виде матрицы. Это и будет рангом матрицы.
Давайте рассмотрим пример. Пусть у нас есть следующая матрица:
A =
| 1 2 3 | | 0 1 2 | | 0 0 1 |
Применяя элементарные преобразования строк, мы получаем следующий ступенчатый вид матрицы:
A' =
| 1 2 3 | | 0 1 2 | | 0 0 1 |
Как видно, мы получили три ненулевые строки в ступенчатом виде. Следовательно, ранг матрицы равен 3.
Таким образом, определение ранга матрицы через определитель сводится к приведению матрицы к ступенчатому виду и подсчету количества ненулевых строк в этом виде.
Правила и примеры вычисления ранга
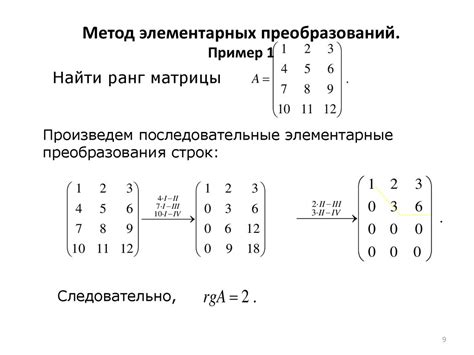
Вот основные правила, которые помогут в вычислении ранга матрицы:
Правило 1:
Если определитель матрицы не равен нулю, то ранг матрицы равен числу её строк (или столбцов).
Правило 2:
Если определитель матрицы равен нулю, то ранг матрицы меньше числа её строк (или столбцов).
Пример 1:
Определим ранг следующей матрицы:
Матрица A:
| 1 2 3 |
| 4 5 6 |
| 7 8 9 |
Вычисляем определитель матрицы A:
det(A) = (1 * (5 * 9 - 6 * 8)) - (2 * (4 * 9 - 6 * 7)) + (3 * (4 * 8 - 5 * 7))
det(A) = (1 * 21) - (2 * (-6)) + (3 * (-3))
det(A) = 21 + 12 - 9 = 24
Так как определитель матрицы A не равен нулю, ранг матрицы A будет равен числу строк (или столбцов), то есть 3.
Пример 2:
Определим ранг следующей матрицы:
Матрица B:
| 1 2 3 |
| 4 5 6 |
| 7 8 9 |
Вычисляем определитель матрицы B:
det(B) = (1 * (5 * 9 - 6 * 8)) - (2 * (4 * 9 - 6 * 7)) + (3 * (4 * 8 - 5 * 7))
det(B) = (1 * 21) - (2 * (-6)) + (3 * (-3))
det(B) = 21 + 12 - 9 = 24
Так как определитель матрицы B не равен нулю, ранг матрицы B будет равен числу строк (или столбцов), то есть 3.
В этих примерах мы видим, что ранг матрицы может быть найден с помощью определителя матрицы и связанных правил.
Метод Гаусса для нахождения ранга матрицы

Шаги метода Гаусса для нахождения ранга матрицы:
- Выбирается первый ненулевой элемент матрицы и делается его главным элементом (то есть элементом, на котором будет выполняться следующая операция).
- Вычитается этот главный элемент из всех элементов строки, на которой он находится, чтобы получить нули внутри этой строки ниже главного элемента.
- Повторяются шаги 1-2 для всех оставшихся строк матрицы, пропуская уже обработанные строки.
- Полученная матрица будет иметь диагональный или ступенчатый вид. Ранг матрицы равен количеству ненулевых строк этой матрицы.
Пример:
Рассмотрим матрицу:
1 2 3
0 4 6
0 0 9
Шаг 1: Главный элемент выбран в первой строке (элемент 1).
1 2 3
0 4 6
0 0 9
Шаг 2: Вычитаем главный элемент из всех элементов ниже него в первой строке.
1 2 3
0 2 3
0 0 9
Шаг 3: Главный элемент выбран во второй строке (элемент 2).
1 2 3
0 2 3
0 0 9
Шаг 4: Вычитаем главный элемент из всех элементов ниже него во второй строке.
1 2 3
0 1 1.5
0 0 9
Шаг 5: Главный элемент выбран в третьей строке (элемент 9).
1 2 3
0 1 1.5
0 0 9
Шаг 6: Вычитаем главный элемент из всех элементов ниже него в третьей строке.
1 2 3
0 1 1.5
0 0 1
Полученная матрица имеет диагональный вид с тремя ненулевыми строками. Следовательно, ранг данной матрицы равен 3.
Алгоритм метода Гаусса
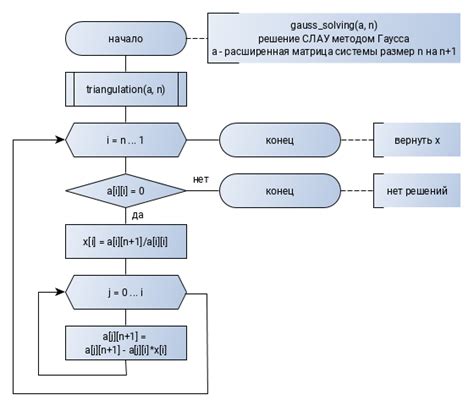
Ниже приведен алгоритм метода Гаусса:
- Выбрать начальную матрицу, состоящую из системы линейных уравнений или исходной матрицы.
- Выбрать первый элемент матрицы (назовем его "главным элементом"), чтобы он был ненулевым. Если такого элемента нет, то это означает, что матрица имеет ранг ноль.
- Если главный элемент не находится на первой строке, выполнить перестановку строк, чтобы главный элемент оказался на первой строке.
- Делить первую строку на значение главного элемента, чтобы привести его к единице.
- Для каждой строки, начиная со второй, вычесть из неё первую строку, умноженную на соответствующий элемент текущей строки, чтобы получить нули под главным элементом.
- Повторить шаги 2-5 для следующего главного элемента, начиная с следующей строки и столбца.
- Повторить шаги 2-6 до тех пор, пока не будет достигнута конечная ступенчатая форма матрицы. Ранг матрицы будет равен количеству ненулевых строк в ступенчатой форме.
Применение метода Гаусса позволяет упростить решение систем линейных уравнений и определить ранг матрицы. Этот метод широко используется в линейной алгебре и математическом анализе.
Примеры вычисления ранга матрицы по методу Гаусса

Рассмотрим матрицу A:
|1 2 3 | |4 5 6 | |7 8 9 |
Применим элементарные преобразования строк и получим матрицу B:
|1 2 3 | |0 -3 -6 | |0 0 0 |
Как видно, последняя строка матрицы B состоит из нулей. Ранг матрицы B равен 2, так как ненулевых строк в ней 2. Следовательно, ранг исходной матрицы A также равен 2.
Рассмотрим матрицу C:
|1 0 1 0 | |0 1 1 0 | |0 0 0 1 |
Применим элементарные преобразования строк и получим матрицу D:
|1 0 1 0 | |0 1 1 0 | |0 0 0 1 |
Матрица D находится в каноническом виде, при этом ее последняя строка не является линейной комбинацией предыдущих строк. Ранг матрицы D равен 3. Следовательно, ранг исходной матрицы C также равен 3.
Таким образом, мы видим, что метод Гаусса позволяет удобно и эффективно определить ранг матрицы. Его основная идея состоит в приведении матрицы к определенному каноническому виду и определении количества ненулевых строк в полученной матрице.
