Задача о нахождении равнодействующей силы трех сил – это одна из основных задач физики. Равнодействующая сила это сумма всех сил, действующих на тело. Определяется она по формуле:
Fрд = √(F12 + F22 + F32 + 2 * F1 * F2 * cosα + 2 * F2 * F3 * cosβ + 2 * F1 * F3 * cosγ)
Где F1, F2 и F3 – это величины сил, а α, β и γ – углы между ними.
Для решения таких задач необходимо выполнять несколько шагов. Во-первых, нужно определить модули сил и углы между ними. Затем, подставить эти значения в формулу и произвести необходимые вычисления. Получив результат, можно определить равнодействующую силу трех сил.
Определение равнодействующей силы

Для определения равнодействующей силы трех сил, действующих на тело, необходимо сложить эти три силы по принципу параллелограмма. Для этого нужно провести параллельные линии от начал точки приложения каждой силы, перпендикулярные этим силам. Затем нужно провести линию от конца первой параллельной линии до конца последней параллельной линии. Эта линия представляет собой равнодействующую силу трех сил.
Представим, что у нас есть три силы F1, F2 и F3, действующие на тело. Мы находим начало каждой силы и проводим параллельные линии
Проводим линию от начала первой параллельной линии до конца последней параллельной линии
Эта линия представляет собой равнодействующую силу (R) трех сил. Вектор равнодействующей силы (R) можно найти путем применения углового метода или метода компонентов, используя треугольники и тригонометрические функции.
Формула для нахождения равнодействующей силы

Равнодействующая сила, также известная как результирующая сила, представляет собой сумму всех действующих на объект сил. Когда на объект действуют несколько сил, чтобы найти равнодействующую силу, мы можем использовать формулу.
Если у нас есть три силы, действующие на объект в трехмерном пространстве, мы можем использовать теорему Пифагора, чтобы найти равнодействующую силу. Формула выглядит следующим образом:
Fр = √(F12 + F22 + F32),
где Fр - равнодействующая сила,
F1, F2, F3 - три силы, действующие на объект.
Таким образом, для определения равнодействующей силы, мы должны найти квадрат каждой силы, складывает их и извлекает квадратный корень от суммы. Полученное значение будет равнодействующей силой.
Примечание: Помните, что в данной формуле силы должны быть векторными величинами. Это означает, что они имеют не только величину, но и направление. Если силы заданы в виде векторов, формула выше применяется без изменений.
Примеры нахождения равнодействующей силы
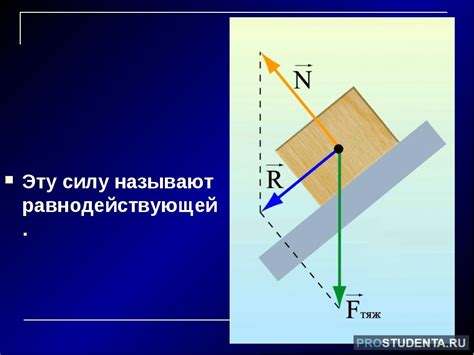
Равнодействующая сила представляет собой сумму всех сил, действующих на объект. Она может быть найдена с помощью графического метода или аналитически, применяя законы векторной алгебры.
Рассмотрим несколько примеров нахождения равнодействующей силы:
- Пример 1
- Пример 2
- Пример 3
На тело, помещенное на горизонтальную поверхность, действуют три силы: сила веса, нормальная сила и сила трения. Чтобы найти равнодействующую этих сил, нужно разложить каждую из них на составляющие, направленные вдоль и перпендикулярно поверхности. Затем сложить все составляющие силы, чтобы получить равнодействующую.
На объект действуют две силы, направленные под углом друг к другу. Чтобы найти равнодействующую этих сил, нужно использовать тригонометрические функции для определения горизонтальной и вертикальной составляющих каждой силы. Затем складываются все горизонтальные и вертикальные составляющие силы для получения равнодействующей.
Две силы действуют на объект в противоположных направлениях. Если известны величины и направления этих сил, можно использовать принцип суперпозиции, сложив векторы сил вместе. Результирующий вектор будет равнодействующей силой.
В каждом из этих примеров важно правильно определить направление и величину сил для нахождения равнодействующей. Это помогает представить силы в виде векторов и использовать алгебраические методы для их сложения.
Графический метод нахождения равнодействующей силы
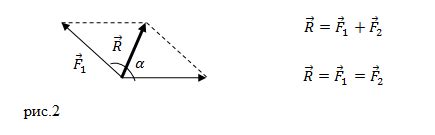
Графический метод нахождения равнодействующей силы используется для определения силы, которая могла бы заменить две или более силы, действующие на тело. С помощью этого метода можно визуализировать силы и определить их общий результат.
В графическом методе нахождения равнодействующей силы необходимо построить векторную диаграмму для каждой силы, указав их направления и величины. Затем нужно найти геометрическую сумму всех построенных векторов. Равнодействующей силы будет являться вектор, который представляет собой результат этой суммы.
Для построения векторной диаграммы силы необходимо выбрать масштаб и направление осей координат и отложить на них вектор силы. Затем следует построить векторы для остальных сил на той же системе координат. Направления векторов силы выбираются с учетом заданной системы координат и указываются стрелками. Величины векторов силы могут быть пропорциональными или масштабированными в соответствии с выбранным масштабом.
| Сила | Величина (N) | Угол (°) |
|---|---|---|
| Сила 1 | 10 | 30 |
| Сила 2 | 15 | 60 |
| Сила 3 | 12 | 120 |
После построения всех векторных диаграмм следует найти их геометрическую сумму. Для этого можно использовать метод параллелограмма, метод треугольника или метод составления замкнутого многоугольника. Выбор метода зависит от точности результата и доступных инструментов. Полученный вектор является равнодействующей силы и представляет собой общий результат суммы действующих сил.
Графический метод нахождения равнодействующей силы позволяет легко визуализировать силы и получить объективный результат. Однако, для более точных результатов рекомендуется использовать математический метод нахождения равнодействующей силы с помощью разложения сил на компоненты по осям.
Применение равнодействующей силы в реальной жизни

В физике равнодействующая сила используется для вычисления и понимания движения тел. Например, при исследовании движения автомобиля по склону можно использовать равнодействующую силу для определения его ускорения и скорости. Это позволяет инженерам и конструкторам разрабатывать более эффективные детали и системы транспортных средств.
В инженерии равнодействующая сила применяется при проектировании и строительстве мостов, зданий и других конструкций. Равнодействующая сила помогает инженерам определить необходимые размеры и прочность материалов, чтобы конструкция выдерживала действующие силы, такие как ветер, гравитация и нагрузка.
В спорте равнодействующая сила имеет важное значение для атлетов. Например, в водном спорте пловцы используют равнодействующую силу для оптимального движения в воде. Также равнодействующая сила применяется в футболе при ударе по мячу или толчке соперника.
В области транспорта равнодействующая сила играет роль в разработке автомобилей, поездов и самолетов. Равнодействующая сила позволяет оптимизировать эффективность движения и потребление топлива, а также учитывать влияние ветра и других факторов на транспортное средство.