Вписанная окружность в квадрат - это окружность, которая проходит через вершины квадрата и имеет радиус, равный половине его стороны. Она является одной из ключевых геометрических фигур и может применяться в широком спектре задач и решений.
Найти сторону квадрата с заданным радиусом вписанной окружности можно с использованием геометрических формул и теорем. Одним из методов является применение формулы, основанной на соотношении радиуса вписанной окружности к стороне квадрата.
По теореме Пифагора можно вывести, что сторона квадрата равна произведению радиуса окружности на корень из двух (a = r * √2), где "a" - сторона квадрата, "r" - радиус вписанной окружности.
Таким образом, для нахождения стороны квадрата с заданным радиусом вписанной окружности необходимо умножить данное значение на корень из двух. Этот подход позволяет получить точное значение стороны квадрата и использовать его для решения различных геометрических задач.
Как найти сторону квадрата
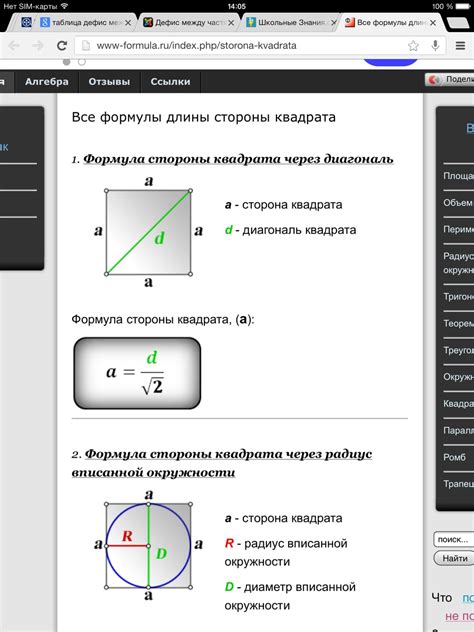
1. По формуле
Есть простая формула, которая позволяет найти сторону квадрата, если известны площадь или периметр:
Сторона квадрата равна квадратному корню из площади квадрата или периметра квадрата.
Например, если нам дана площадь квадрата S, то сторона квадрата a может быть найдена по формуле:
a = sqrt(S)
А если нам дан периметр квадрата P, то сторона квадрата a может быть найдена по формуле:
a = P / 4
2. По диагонали
В квадрате все стороны равны между собой, а также все диагонали равны. Если известна диагональ квадрата, то мы можем легко найти сторону.
Сторона квадрата равна длине диагонали, поделенной на √2:
a = d / √2
Где d - длина диагонали.
Используя эти простые формулы, вы можете легко найти сторону квадрата в различных ситуациях.
Описание задачи

Дана задача на нахождение стороны квадрата, в который вписана окружность с заданным радиусом. Задача заключается в том, чтобы найти длину стороны квадрата при известном радиусе вписанной окружности.
Для решения этой задачи можно использовать определенную формулу. По свойству квадрата, его диагональ равна удвоенному радиусу вписанной окружности. Следовательно, сторона квадрата будет равна диагонали, деленной на корень из двух.
В математической записи данная формула будет выглядеть следующим образом:
сторона_квадрата = (2 * радиус_вписанной_окружности) / корень_из_двух
Таким образом, для решения задачи нужно подставить значение радиуса вписанной окружности в данную формулу и вычислить результат.
Требования к задаче

Для решения задачи "Как найти сторону квадрата с радиусом вписанной окружности" требуется знание основных математических понятий и формул, таких как площадь, диаметр, радиус и теорема Пифагора. Также необходимо умение работать со сравнением чисел и выполнением арифметических операций.
Для решения задачи потребуется применить следующие шаги:
| Шаг 1: | Найти диаметр вписанной окружности. |
| Шаг 2: | Найти радиус вписанной окружности. |
| Шаг 3: | Вычислить площадь квадрата, зная радиус вписанной окружности. |
| Шаг 4: | Найти сторону квадрата, используя площадь квадрата. |
Для успешного решения задачи необходимо внимательно следовать каждому шагу и производить все вычисления с высокой точностью. Необходимо обращать внимание на геометрические свойства фигур и использовать соответствующие теоремы для нахождения ответа.
Формула нахождения стороны квадрата

Чтобы найти сторону квадрата, в котором вписана окружность с заданным радиусом, можно использовать следующую формулу:
- Найдем диаметр окружности, используя формулу диаметра: D = 2r, где r - радиус окружности.
- Диаметр окружности равен стороне квадрата, так как квадрат вписан в окружность.
- Таким образом, сторона квадрата равна диаметру окружности.
Итак, формула нахождения стороны квадрата: a = 2r, где a - сторона квадрата, r - радиус окружности.
Подставив известное значение радиуса, получим длину стороны квадрата.
Пример решения задачи

Для того чтобы найти сторону квадрата с радиусом вписанной окружности, нужно использовать известную формулу:
Сторона квадрата = 2 * радиус окружности
Допустим, мы знаем, что радиус вписанной окружности равен 4 единицам длины. Тогда сторона квадрата будет:
Сторона квадрата = 2 * 4 = 8 единиц длины
Таким образом, сторона квадрата, в который вписана окружность радиусом 4 единицы, будет равна 8 единицам длины.
Зачем нужно знать сторону квадрата
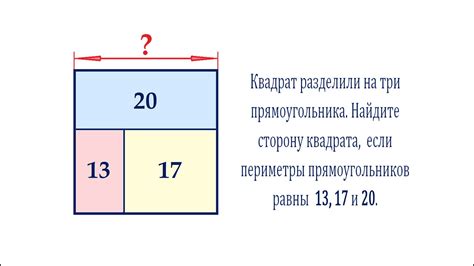
1. Упрощение вычислений
Изучение стороны квадрата с радиусом вписанной окружности позволяет упростить вычисления в различных геометрических задачах. Зная эту величину, можно легко определить другие параметры: площадь квадрата, длину его диагонали, периметр и т.д. Это делает решение задач более эффективным и быстрым.
2. Решение задач на построение
Часто в геометрии возникают задачи на построение геометрических фигур. Знание стороны квадрата позволяет легко построить этот квадрат с помощью циркуля и линейки. Например, если известна сторона квадрата и нужно построить окружность с радиусом, равным стороне квадрата, можно использовать его сторону в качестве радиуса для построения окружности.
3. Применение в реальной жизни
Знание стороны квадрата может быть полезно в повседневной жизни. Например, оно может быть использовано при проектировании или строительстве зданий и сооружений. Также эту информацию можно применить при расчете площадей помещений, оценке загруженности площади и многих других ситуациях, связанных с геометрией.
В итоге, знание стороны квадрата с радиусом вписанной окружности является важным и полезным инструментом для решения задач и применения геометрических знаний в реальной жизни.
Применение задачи в реальной жизни

Знание формулы для вычисления стороны квадрата, в который вписана окружность, может быть полезным во многих ситуациях. Например, инженеры и архитекторы могут использовать эту формулу для расчета размеров основания строения или для размещения объектов внутри квадратной площади.
Также, зная сторону квадрата с радиусом вписанной окружности, можно получить практическую пользу при решении геометрических задач. Например, можно использовать эту информацию для определения расстояния между центром окружности и его точкой касания с стороной квадрата.
- Вписанная окружность в квадрат делит его стороны пополам.
- Сторона квадрата равна удвоенному радиусу вписанной окружности.
- Формула для нахождения стороны квадрата: сторона = 2 * радиус.
- Найти сторону квадрата с радиусом вписанной окружности можно, зная значение радиуса.