Прямоугольный треугольник - одна из самых важных и распространенных геометрических фигур. Он имеет один прямой угол (равный 90 градусам) и два других угла, которые всегда суммируются до 90 градусов. Также прямоугольный треугольник имеет две стороны, из которых одна является гипотенузой - самой длинной стороной, которая напротив прямого угла.
Теорема Пифагора - основополагающая теорема для прямоугольных треугольников, которая позволяет нам вычислять длину любой стороны или находить значения тригонометрических функций для углов. В этой статье мы рассмотрим, как найти тангенс угла прямоугольного треугольника по его сторонам.
Тангенс угла прямоугольного треугольника определяется как отношение противолежащей стороны к прилежащей стороне. Для нахождения тангенса угла необходимо знать значения противолежащей и прилежащей сторон. Просто поделите значение противолежащей стороны на значение прилежащей стороны и получите результат в виде десятичной дроби или числа.
Что такое тангенс угла?
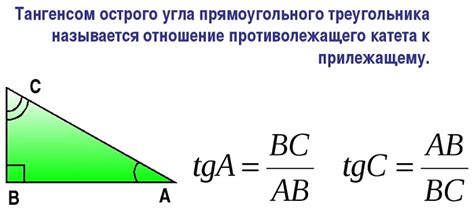
Тангенс угла обозначается как tg или tan. Он определяется формулой:
tg(α) = a/b,
где α - угол, a - противоположная сторона, b - прилежащая сторона.
Значение тангенса угла может быть положительным, отрицательным или равным нулю в зависимости от четверти, в которой находится угол в декартовой системе координат.
Зная значения прилежащей и противоположной сторон треугольника, можно использовать тангенс угла для вычисления величины самого угла. Для этого необходимо применить обратную функцию арктангенс:
α = arctg(a/b).
Тангенс угла широко применяется в геометрии, физике, инженерии и других науках. Он позволяет решать задачи, связанные с построением, измерением и расчетами треугольников.
Как вычислить тангенс угла?

Для вычисления тангенса угла требуется знать длину противолежащей стороны и длину прилежащей стороны. Формула для вычисления тангенса угла прямоугольного треугольника выглядит следующим образом:
тангенс угла = противолежащая сторона / прилежащая сторона
Например, пусть противолежащей стороной является сторона А, а прилежащей стороной - сторона В. Тогда формула для вычисления тангенса угла будет выглядеть следующим образом:
тангенс угла = А / В
Вычисление тангенса угла может быть полезно при решении задач в геометрии и физике, а также в других областях науки и техники.
Обратите внимание, что значения сторон должны быть положительными числами. Также следует учитывать, что некоторые калькуляторы и программы могут требовать ввода угла в радианах, поэтому необходимо быть осторожным при использовании тангенса в различных контекстах.
Формула для вычисления тангенса

Тангенс угла прямоугольного треугольника может быть вычислен по формуле:
| Формула | Описание | |||
|---|---|---|---|---|
| тангенс угла | = | противоположная сторона | / | прилежащая сторона |
В данной формуле тангенс угла представляет отношение противоположной стороны к прилежащей стороне треугольника. Противоположная сторона – это сторона, которая не прилегает к углу, для которого вычисляется тангенс. Прилежащая сторона – это сторона, которая прилегает к углу.
Используя данную формулу, вы можете легко вычислить тангенс угла прямоугольного треугольника по известным значениям сторон.
Как найти длину противоположной и прилежащей сторон треугольника?

Для расчета длины противоположной и прилежащей сторон прямоугольного треугольника можно использовать теорему Пифагора. Теорема Пифагора утверждает, что в прямоугольном треугольнике с катетами (прилежащими сторонами) a и b и гипотенузой (противоположной стороной) c, сумма квадратов катетов равна квадрату гипотенузы. Это можно записать формулой:
a2 + b2 = c2
Для нахождения длины противоположной и прилежащей сторон треугольника по данной формуле следует:
- Известные значения сторон треугольника обозначить как a и b.
- Вычислить значение гипотенузы по формуле c = √(a2 + b2).
- По значению гипотенузы можно определить искомую длину противоположной и прилежащей сторон. Например, если известны длина гипотенузы и противоположной стороны, то для нахождения прилежащей стороны воспользуйтесь выражением a = √(c2 - b2).
Таким образом, применение теоремы Пифагора позволяет найти длину противоположной и прилежащей сторон прямоугольного треугольника.
Вычисление тангенса по формуле

Тангенс угла прямоугольного треугольника можно вычислить, используя формулу:
тангенс угла = противоположная сторона / прилежащая сторона
Для этого необходимо знать значения этих сторон треугольника. Противоположная сторона - это сторона, которая напротив угла, для которого хотим найти тангенс. Прилежащая сторона - это сторона, которая соединяет данный угол с прямым углом.
Сначала находим значения сторон треугольника, затем подставляем их в формулу и выполняем вычисления. Результат будет тангенсом заданного угла.
Например, если противоположная сторона равна 5, а прилежащая сторона равна 3, то тангенс угла равен:
тангенс угла = 5 / 3 = 1.67
Таким образом, тангенс выбранного угла будет равен 1.67.
Как использовать калькулятор для вычисления тангенса?
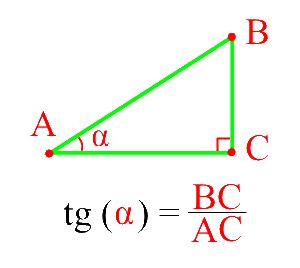
Для использования калькулятора для вычисления тангенса угла, следуйте следующим шагам:
- Включите калькулятор и убедитесь, что на нем доступны математические функции, включая тангенс.
- Введите значение стороны, противолежащей углу, в соответствующее поле.
- Введите значение стороны, прилежащей углу, в соответствующее поле.
- Найдите кнопку или функцию, обозначенную тангенсом, и нажмите ее.
Калькулятор автоматически вычислит значение тангенса угла с заданными сторонами треугольника и отобразит результат на экране. Обратите внимание, что результат может быть представлен в виде десятичной дроби или десятичного значения.
Если вы не можете найти функцию тангенса на калькуляторе или не уверены в правильности вычислений, можно воспользоваться онлайн-калькулятором или математическим программным обеспечением, где доступны широкие возможности для вычисления тангенса и других математических функций.
Приложения тангенса в геометрии и физике
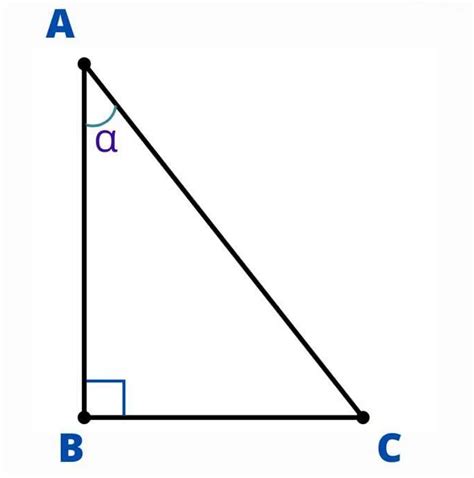
В геометрии тангенс используется, например, для нахождения значения углов, когда известны стороны прямоугольного треугольника. Для этого можно воспользоваться формулой: тангенс угла равен отношению противоположной стороны к прилежащей стороне. Таким образом, тангенс позволяет определить размеры углов и сторон треугольника, что важно при решении геометрических задач и построении графиков функций.
В физике тангенс применяется для решения задач, связанных с движением искусственных спутников Земли, ракет и других объектов, движущихся по криволинейным траекториям. Также тангенс используется при измерении углов наклона поверхностей, например, при определении угла наклона плоскости накопителя солнечной энергии для оптимального использования солнечного света.
Более подробное рассмотрение применения тангенса можно найти в области тригонометрии, где эта функция является одной из ключевых.
- В геометрии тангенс используется для решения задач по построению треугольников, определению углов наклона и определению проекций.
- В физике тангенс используется для измерения углов наклона, определения движения объектов и решения задач динамики.
- В астрономии тангенс используется для вычисления углов наклона планет и спутников.
- В инженерии тангенс используется для проектирования и расчета конструкций, определения углов наклона и расчета нагрузок.
Тангенс является мощным инструментом для решения разнообразных задач в геометрии и физике. Понимание его принципов и применение помогает в решении сложных задач подобного рода и нахождении нужных решений.
Примеры вычисления тангенса угла в задачах
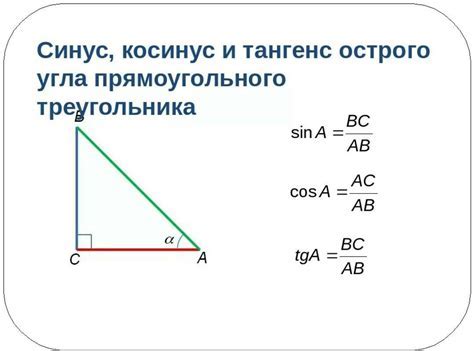
Рассмотрим несколько задач, в которых требуется вычислить тангенс угла прямоугольного треугольника по его сторонам:
Пример 1:
Дано: прямоугольный треугольник со сторонами a = 3 и b = 4.
Найти: тангенс угла α.
Решение:
В данном случае, угол α является противолежащим углом катета a, поэтому его тангенс можно найти как tg(α) = a/b.
Подставляя значения, получаем: tg(α) = 3/4.
Ответ: tg(α) = 0.75.
Пример 2:
Дано: прямоугольный треугольник со сторонами a = 5 и c = 13.
Найти: тангенс угла β.
Решение:
В данном случае, угол β является противолежащим углом катета a, поэтому его тангенс можно найти как tg(β) = a/c.
Подставляя значения, получаем: tg(β) = 5/13.
Ответ: tg(β) ≈ 0.38.
Пример 3:
Дано: прямоугольный треугольник со сторонами b = 8 и c = 17.
Найти: тангенс угла γ.
Решение:
В данном случае, угол γ является противолежащим углом катета b, поэтому его тангенс можно найти как tg(γ) = b/c.
Подставляя значения, получаем: tg(γ) = 8/17.
Ответ: tg(γ) ≈ 0.47.