В 7 классе ученики начинают изучать алгебру и графики функций. Одна из важных тем, которую они изучают, это линейные зависимости. Линейная зависимость представляет собой отношение между двумя переменными, которое можно представить графиком в виде прямой линии.

Как найти уравнение функции по графику линейной зависимости? Для этого необходимо определить коэффициенты a и b. Коэффициент a (наклон прямой) показывает, на сколько единиц меняется зависимая переменная при изменении независимой переменной на одну единицу. Коэффициент b (свободный член) указывает значение зависимой переменной при независимой переменной, равной нулю.

Для определения коэффициента a, необходимо выбрать две точки на графике и найти их координаты. Затем нужно вычислить изменение зависимой переменной и изменение независимой переменной между этими двумя точками. Коэффициент a равен отношению изменения зависимой переменной к изменению независимой переменной.

Как найти уравнение функции

Уравнение функции позволяет представить математическую зависимость между переменными в виде формулы. Нахождение уравнения функции может быть полезно для анализа данных, прогнозирования результатов и решения различных задач. В данной статье рассмотрим, как найти уравнение функции по графику линейной зависимости в 7 классе.

1. Построение графика. Необходимо иметь график линейной зависимости, состоящий из отдельных точек, которые лежат на одной прямой.

2. Определение коэффициента наклона. Для этого нужно выбрать две точки на графике, затем посчитать разность их y-координат и разность их x-координат. Полученные значения являются соответственно изменением по оси y и изменением по оси x. Коэффициент наклона равен отношению изменения по оси y к изменению по оси x.

3. Определение свободного члена. Для этого необходимо выбрать одну из точек на графике и подставить ее координаты, а также коэффициент наклона в общее уравнение линейной функции y = kx + b. Подставляем значений y и x и находим b.

Таким образом, уравнение функции определяется соотношением y = kx + b, где k - коэффициент наклона, а b - свободный член.

Где искать

Для нахождения уравнения функции по графику линейной зависимости в 7 классе можно воспользоваться несколькими источниками информации:

1. Учебник по математике. Перед началом поиска рекомендуется обратиться к учебнику по математике для 7 класса. В учебнике обычно даются основные определения и правила, которые помогут вам понять, как найти уравнение функции по графику. Также в учебнике могут быть приведены примеры решения подобных задач.

2. Онлайн-ресурсы. В интернете можно найти множество онлайн-ресурсов, которые помогут вам разобраться в данной теме. Некоторые из них предлагают подробные объяснения с примерами, а другие предлагают интерактивные задания и тесты для самопроверки.

3. Учитель или репетитор. Если у вас остались вопросы после самостоятельного изучения темы, вы всегда можете обратиться к своему учителю или репетитору по математике. Они смогут дать вам дополнительные объяснения и помочь решить задачи.

Важно помнить, что для успешного нахождения уравнения функции по графику линейной зависимости в 7 классе необходимо понимать основные понятия и правила алгебры, в том числе нахождение коэффициентов уравнения прямой, используя координаты двух точек на графике.

Что такое уравнение функции

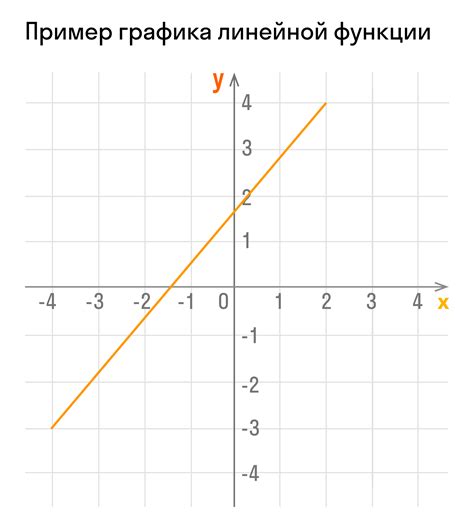
Уравнение функции в общем виде имеет вид: y = f(x), где y - значение зависимой переменной, x - значение независимой переменной, f - функция, определенная для данного уравнения.

Уравнение функции может быть представлено в различных формах, в зависимости от типа функции и предмета задачи. Например:

• Для линейной функции y = kx + b, где k и b - коэффициенты, определяющие наклон и сдвиг графика функции.
• Для квадратичной функции y = ax^2 + bx + c, где a, b и c - коэффициенты, определяющие форму и положение графика функции.
• Для экспоненциальной функции y = a*b^x, где a и b - коэффициенты, определяющие форму и поведение графика функции.

Уравнение функции позволяет не только описывать зависимость между переменными, но и находить значения зависимой переменной, если известно значение независимой переменной. Это удобно при решении различных задач и анализе данных.

Как найти уравнение по графику

Для того чтобы найти уравнение функции по графику линейной зависимости, необходимо знать две точки на графике. Лучше всего выбрать точки, через которые проходит прямая линия.

Шаги для определения уравнения функции по графику:

1. Выбрать две точки, через которые проходит прямая линия на графике. Обозначим их координаты как (x₁, y₁) и (x₂, y₂).
2. Найти угловой коэффициент, используя формулу: m = (y₂ - y₁) / (x₂ - x₁).
3. Найти уравнение функции, используя формулу: y = mx + b, где m - угловой коэффициент, b - свободный член.
4. Найти свободный член, подставив координаты одной из точек в уравнение и решив его относительно b.

Пример:

• Допустим, что мы выбрали точки (1, 2) и (3, 4) на графике линейной зависимости.
• Угловой коэффициент равен: m = (4 - 2) / (3 - 1) = 2 / 2 = 1.
• Таким образом, уравнение функции будет иметь вид: y = 1x + b.
• Подставив значения (1, 2) в уравнение, получаем: 2 = 1*1 + b.
• Решив уравнение относительно b, получаем: b = 1.
• Таким образом, уравнение функции будет иметь вид: y = x + 1.

Теперь вы знаете, как найти уравнение функции по графику линейной зависимости в 7 классе. Этот метод можно использовать для нахождения уравнений других линейных функций, используя разные точки на графике. Помните, что чем точнее выбраны точки, тем более точное будет уравнение функции.

Примеры нахождения уравнения функции

Найти уравнение функции по графику линейной зависимости в 7 классе можно с помощью нескольких простых шагов. Рассмотрим несколько примеров.

Пример 1:

Пусть дан график функции, представляющей линейную зависимость. Из графика видно, что прямая проходит через точку (2, 3) и (4, 7). Чтобы найти уравнение этой функции, необходимо найти коэффициенты уравнения прямой y = ax + b.

Используя эти две точки, можно составить систему уравнений:

3 = 2a + b (1)

7 = 4a + b (2)

Решив эту систему уравнений, найдем значения a и b. Решение этой системы будет являться уравнением функции, которую мы ищем.

Пример 2:

Пусть дан график функции, представляющей линейную зависимость. Из графика видно, что прямая проходит через точку (1, 4) и (3, 10). Чтобы найти уравнение этой функции, снова необходимо найти коэффициенты уравнения прямой y = ax + b.

Используя эти две точки, можно составить систему уравнений:

4 = a + b (1)

10 = 3a + b (2)

Решив эту систему уравнений, найдем значения a и b. Решение этой системы будет являться уравнением функции, которую мы ищем.

Таким образом, для нахождения уравнения функции по графику линейной зависимости необходимо составить систему уравнений, используя известные точки на графике, и решить ее для нахождения коэффициентов a и b. Решение будет представлять собой искомое уравнение функции.