Треугольник - это геометрическая фигура, которая состоит из трех сторон и трех вершин. Вершины - это точки, в которых стороны треугольника пересекаются. Они образуют углы между сторонами и определяют форму треугольника. Каждая вершина имеет свои координаты и обозначается буквами A, B и C. Чтобы найти вершины треугольника, необходимо знать длины его сторон или иметь информацию о его углах.
Строение треугольника также определяется сторонами - это отрезки, которые соединяют две вершины. Стороны обозначаются маленькими буквами a, b и c. Длины сторон также могут быть различными и влияют на форму треугольника. Стороны могут быть равными (равнобедренный треугольник) или разными (разносторонний треугольник).
Таким образом, чтобы определить положение вершин и сторон треугольника, необходимо обладать информацией об углах и/или длинах сторон. Зная координаты вершин и длины сторон, можно строить треугольник на плоскости и определить его форму и размеры. Знание этих принципов поможет вам лучше понимать геометрию и решать задачи связанные с треугольниками.
Определение треугольника и его вершин
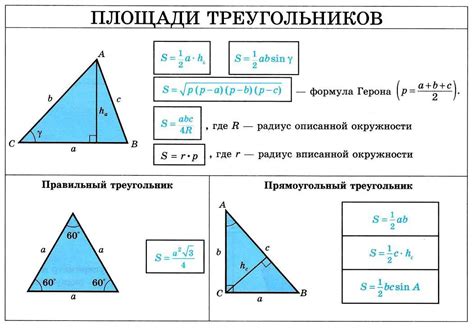
Точка A - первая вершина треугольника, точка B - вторая вершина, а точка C - третья вершина. Вершины определяют положение треугольника в пространстве и являются ключевыми элементами для его изучения.
Если в треугольнике стороны имеют разную длину, то такой треугольник называется разносторонним. Если две стороны треугольника имеют одинаковую длину, то такой треугольник называется равнобедренным. А если все три стороны равны по длине, то треугольник называется равносторонним.
Знание вершин и свойств треугольника помогает определить его тип, строить его и решать задачи, связанные с этой геометрической фигурой. Поэтому важно уметь находить вершины треугольника и понимать их значение в геометрии.
Что такое треугольник и какие у него есть вершины
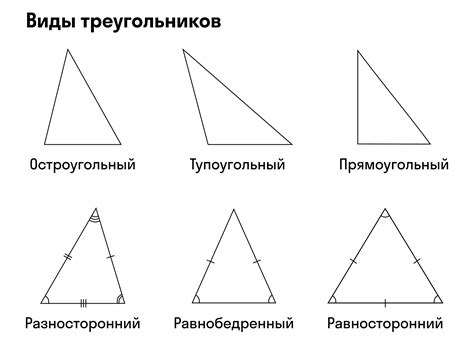
У треугольника есть три вершины, которые обозначаются заглавными буквами. Как правило, используются буквы A, B и C. Вершины треугольника определяют его форму и положение в пространстве.
Вершины треугольника – это точки, где пересекаются его стороны. Каждая вершина обладает координатами на плоскости или в пространстве и может быть представлена в виде упорядоченной пары или тройки чисел.
Например, у треугольника ABC его вершины могут быть представлены точками А(x1, y1), В(x2, y2) и С(x3, y3).
Вершины треугольника имеют большое значение при решении различных задач и вычислений в геометрии.
Расположение сторон треугольника
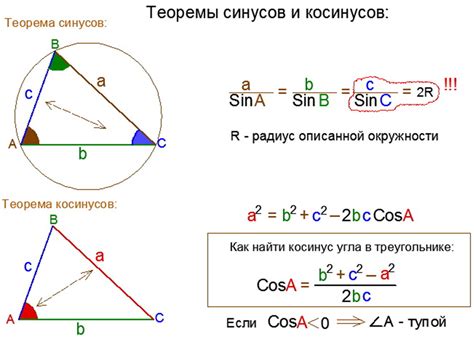
Строение треугольника включает в себя три стороны и три вершины. Стороны треугольника соединяют вершины между собой и определяют его форму и размеры.
Первая сторона треугольника – это отрезок, соединяющий первую и вторую вершины треугольника. Он обозначается как AB.
Вторая сторона треугольника – это отрезок, соединяющий вторую и третью вершины треугольника. Он обозначается как BC.
Третья сторона треугольника – это отрезок, соединяющий третью и первую вершины треугольника. Он обозначается как AC.
Важно помнить, что в треугольнике сумма длин двух его сторон всегда больше длины третьей стороны.
Знание расположения и взаимного положения сторон треугольника необходимо для решения задач по геометрии, построения треугольника и вычисления его характеристик.
Как определить и нарисовать стороны треугольника
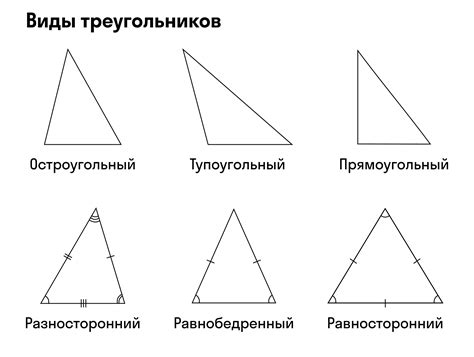
Для определения сторон треугольника необходимо знать координаты его вершин. Каждая вершина треугольника имеет свои координаты на плоскости. Сторона треугольника - это отрезок, соединяющий две вершины.
Координаты вершин треугольника могут быть заданы в различных системах координат, например, в декартовой системе координат, где каждая вершина задается парой чисел (x, y), где x - это значение по оси абсцисс, а y - значение по оси ординат.
Для рисования сторон треугольника, необходимо знать координаты его вершин и использовать соответствующую графическую библиотеку или программу для рисования на плоскости. Например, в HTML можно использовать тег <canvas> и JavaScript для рисования треугольника по заданным координатам вершин.
Нахождение вершин треугольника
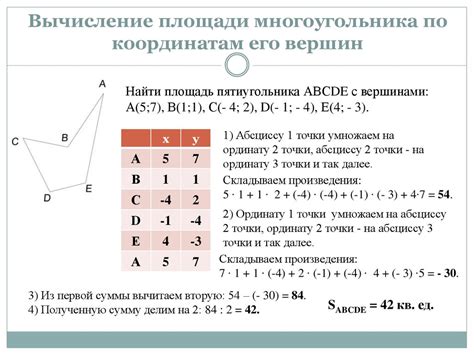
Для нахождения вершин треугольника необходимо знать его характеристики, такие как длины сторон и значения углов. Существуют несколько способов определения вершин треугольника в зависимости от того, какая информация доступна.
1. Если известны длины всех трех сторон треугольника, можно воспользоваться теоремой косинусов. Данная теорема позволяет вычислить значения углов треугольника, а затем с помощью этих значений определить координаты вершин с помощью геометрических вычислений.
2. Если известны длины двух сторон и угол между ними, можно воспользоваться теоремой синусов. Также с помощью геометрических вычислений можно определить координаты вершин треугольника.
3. Если известны координаты двух вершин треугольника и длина одной стороны, можно использовать формулу прямоугольного треугольника для нахождения координат оставшейся вершины.
| Способ нахождения вершин | Необходимые данные |
|---|---|
| Теорема косинусов | Длины всех трех сторон треугольника |
| Теорема синусов | Длины двух сторон и угол между ними |
| Формула прямоугольного треугольника | Координаты двух вершин и длина одной стороны |
Каждый из этих способов имеет свои особенности и подходит для различных ситуаций. Важно учитывать, что для точного определения вершин треугольника необходимо иметь достаточно информации о его характеристиках.
Методы определения координат вершин треугольника
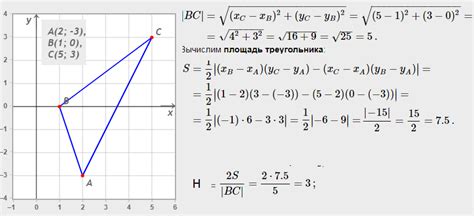
Один из самых распространенных методов - использование координатных плоскостей. Для этого обычно выбирают две оси - горизонтальную и вертикальную, и задают начальные координаты вершин треугольника. Затем, используя данные о длинах сторон треугольника и теорему Пифагора, можно вычислить координаты оставшихся вершин.
Еще один метод - использование векторов. Векторы представляют собой отрезки на плоскости, которые имеют направление и длину. Для определения координат вершин треугольника с помощью векторов необходимо иметь информацию о длинах сторон треугольника и координатах одной из вершин. Затем, используя соотношения между векторами и теорему косинусов, можно вычислить координаты остальных вершин треугольника.
Также существует метод, основанный на использовании матриц. В этом случае, для определения координат вершин треугольника используется матрица, состоящая из коэффициентов уравнений прямых, на которых лежат стороны треугольника. С помощью матричных операций можно вычислить координаты вершин треугольника.
В общем случае, выбор метода определения координат вершин треугольника зависит от имеющихся данных и условий задачи. Каждый метод имеет свои особенности и применяется в разных ситуациях. Важно понимать, что определение координат вершин треугольника является важным шагом в решении геометрических задач и требует внимательности и точности.
Способы нахождения сторон треугольника
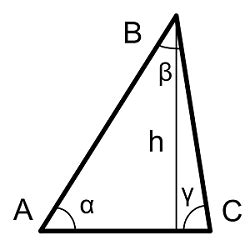
Строение треугольника состоит из трех сторон, каждая из которых играет свою роль в определении его формы и свойств.
Существует несколько способов нахождения сторон треугольника:
1. Известны длины всех сторон. В этом случае нахождение сторон треугольника не вызывает трудностей - просто используйте известные значения для проведения необходимых вычислений.
2. Известны длины двух сторон и угол между ними. Для нахождения третьей стороны треугольника вам понадобится знание тригонометрии. С помощью теоремы косинусов (c^2 = a^2 + b^2 - 2*a*b*cos(alpha)) можно найти длину третьей стороны.
3. Известны длины одной стороны и двух высот, опущенных на нее. Если известна длина стороны треугольника и две высоты, опущенные на эту сторону, можно воспользоваться формулой Герона (S = sqrt(p*(p-a)*(p-b)*(p-c))), где p - полупериметр треугольника, a, b, c - стороны треугольника, а S - его площадь.
4. Известны длины двух сторон и высота, опущенная на одну из них. В этом случае, зная длины сторон треугольника и его высоту, можно вычислить его площадь по формуле (S = 0.5 * a * h), где a - сторона треугольника, h - высота, а S - площадь треугольника.
Важно помнить, что для нахождения сторон треугольника необходимо знать хотя бы некоторые из его характеристик. Используйте эти способы с учетом информации, полученной из задачи или из других источников.