Треугольник - одна из наиболее известных и изучаемых геометрических фигур. Однако мало кто знает, что существует множество разновидностей треугольников, и их вид может быть определен не только по длинам сторон, но и по значениям углов.
Определение вида треугольника по его углам позволяет более точно классифицировать эту фигуру и устанавливать различные свойства и закономерности, которые имеют место для конкретного типа треугольника.
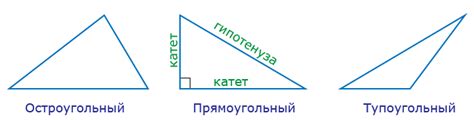
Треугольники классифицируются по величине их углов на остроугольные, прямоугольные и тупоугольные. Остроугольный треугольник - это треугольник, все углы которого острые, то есть меньше 90 градусов. Прямоугольный треугольник имеет один прямой угол величиной 90 градусов. Тупоугольный треугольник содержит один угол с величиной более 90 градусов.
Как узнать вид треугольника по углам
Для определения вида треугольника по углам, необходимо знать значения всех трех углов треугольника. Для этого можно использовать следующий алгоритм:
- Измерьте все углы треугольника с помощью транспортира.
- Запишите значения измеренных углов.
- Сложите значения измеренных углов.
- Проверьте полученную сумму углов треугольника:
- Если сумма углов равна 180°, значит треугольник является плоским.
- Если сумма углов меньше 180°, значит треугольник остроугольный.
- Если сумма углов больше 180° и меньше 360°, значит треугольник тупоугольный.
- Если сумма углов равна 360°, значит треугольник вырожденный.
Таким образом, зная значения углов треугольника, можно определить его вид и классифицировать как остроугольный, тупоугольный или прямоугольный.
Основные свойства треугольников
1. Основные классификации треугольников:
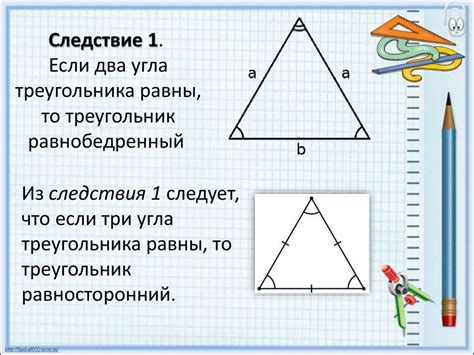
- Равносторонний треугольник: все три стороны равны, а все три угла равны 60 градусов;
- Равнобедренный треугольник: две стороны равны, а два угла равны;
- Разносторонний треугольник: все три стороны и все три угла различны;
2. Сумма углов треугольника:
Всегда сумма всех углов треугольника равна 180 градусов.
3. Неравенство треугольника:
Сумма любых двух сторон треугольника всегда больше третьей стороны.
4. Теорема Пифагора:
Если треугольник является прямоугольным, то квадрат длины гипотенузы равен сумме квадратов длин катетов.
5. Высоты треугольника:
Высоты треугольника - это перпендикулярные отрезки, опущенные из вершин на противолежащие стороны.
Эти основные свойства помогают определить различные виды треугольников и использовать их в геометрических вычислениях и задачах.
Тупоугольный треугольник

Такой треугольник имеет два остроугольных угла, которые суммарно составляют менее 90 градусов.
Для определения тупоугольного треугольника нужно измерить все его углы и проверить условие: если какой-то из углов больше 90 градусов, то треугольник является тупоугольным.
Ниже приведена таблица с примером тупоугольного треугольника и его углами:
| Углы треугольника | |
|---|---|
| Угол A | 60 градусов |
| Угол B | 120 градусов |
| Угол C | 60 градусов |
Остроугольный треугольник
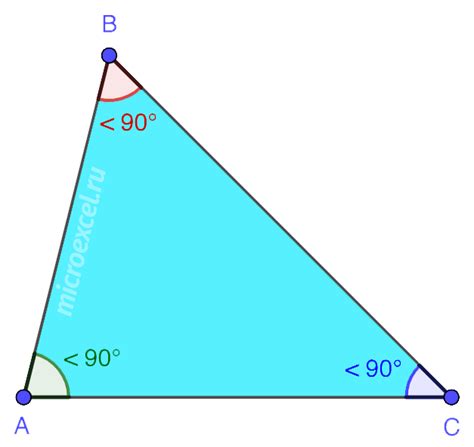
Чтобы определить, является ли треугольник остроугольным, необходимо измерить все его углы. Если все углы треугольника оказываются меньше 90 градусов, значит он является остроугольным.
Остроугольный треугольник имеет следующие свойства:
| Стороны | Углы |
| Все стороны положительны и могут быть разной длины. | Все углы меньше 90 градусов. |
| Сумма длин любых двух сторон треугольника больше длины третьей стороны. | Сумма всех углов треугольника равна 180 градусам. |
| Остроугольный треугольник может быть правильным или неправильным. | Остроугольный треугольник может иметь равные или разные углы. |
Остроугольные треугольники обладают рядом свойств и представляют интерес в геометрических и математических задачах. Изучение их свойств является важной задачей для понимания геометрии и ее приложений.
Прямоугольный треугольник

В прямоугольном треугольнике гипотенуза, то есть наибольшая сторона, всегда противоположна прямому углу. Она является диагональю прямоугольного треугольника и соединяет две остальные стороны, которые являются катетами. Катеты образуют прямой угол и всегда являются меньшими сторонами треугольника.
Основное свойство прямоугольного треугольника - теорема Пифагора, которая гласит, что квадрат длины гипотенузы равен сумме квадратов длин катетов. Это свойство широко применяется в геометрии и физике для решения задач и нахождения неизвестных значений в треугольниках.
Прямоугольные треугольники встречаются в различных ситуациях и областях науки. Например, для вычисления расстояний в навигации, для измерения углов в инженерии, для построения трехмерных моделей и других приложений. Умение определить прямоугольный треугольник по углам помогает правильно анализировать и решать задачи с треугольниками в различных ситуациях.
Специальные случаи треугольников

В дополнение к основным видам треугольников, существуют специальные случаи треугольников, которые имеют уникальные свойства и особенности.
1. Равносторонний треугольник - это треугольник, у которого все стороны равны. Каждый угол равен 60 градусам. Он также является равноугольным треугольником.
2. Равнобедренный треугольник - это треугольник, у которого две стороны равны. Две угловых стороны называются равными сторонами, а оставшаяся сторона - неравная сторона. Равнобедренный треугольник имеет один угол, который отличается от других двух.
3. Прямоугольный треугольник - это треугольник, у которого один из углов равен 90 градусам. В прямоугольном треугольнике сторона, противолежащая прямому углу, называется гипотенузой, а две оставшиеся стороны - катетами.
4. Остроугольный треугольник - это треугольник, у которого все углы острые, то есть меньше 90 градусов.
5. Тупоугольный треугольник - это треугольник, у которого один из углов больше 90 градусов.
Знание специальных случаев треугольников позволяет определить и исследовать различные свойства треугольников в зависимости от их угловых отношений.